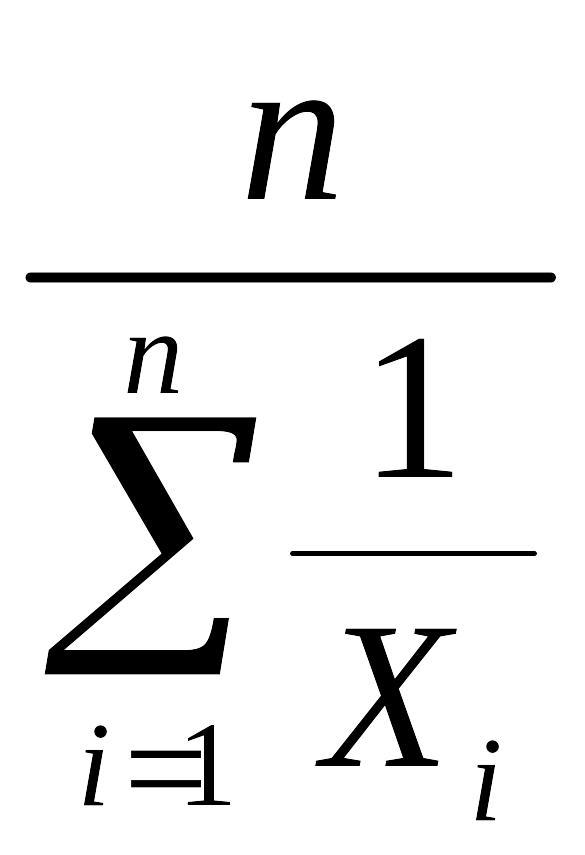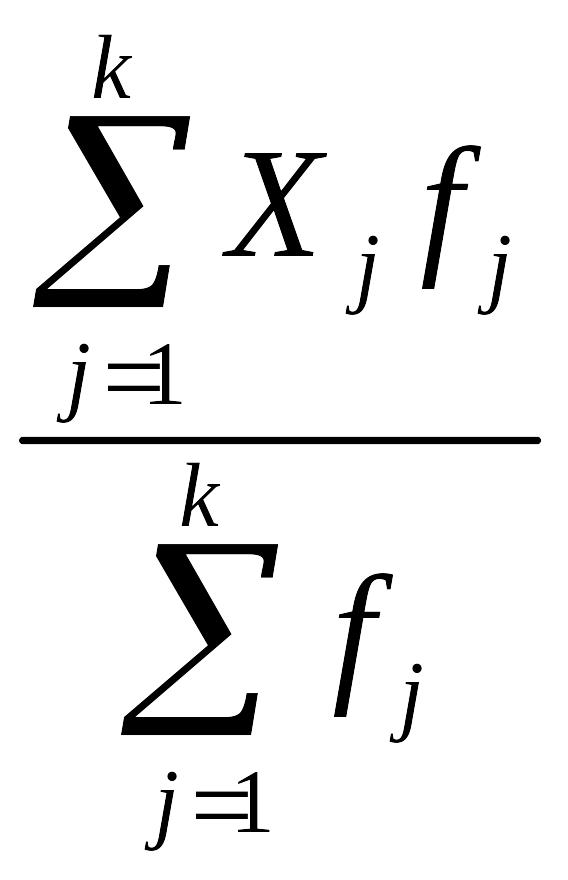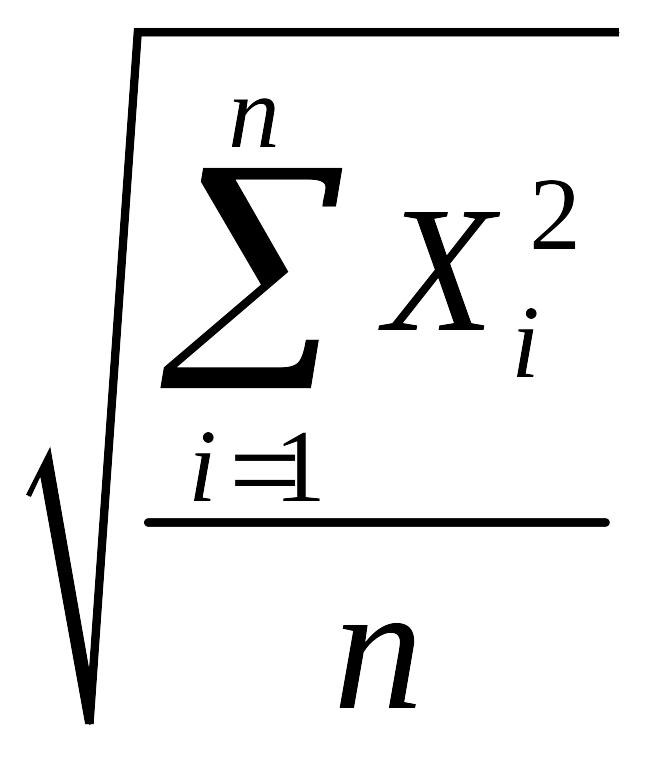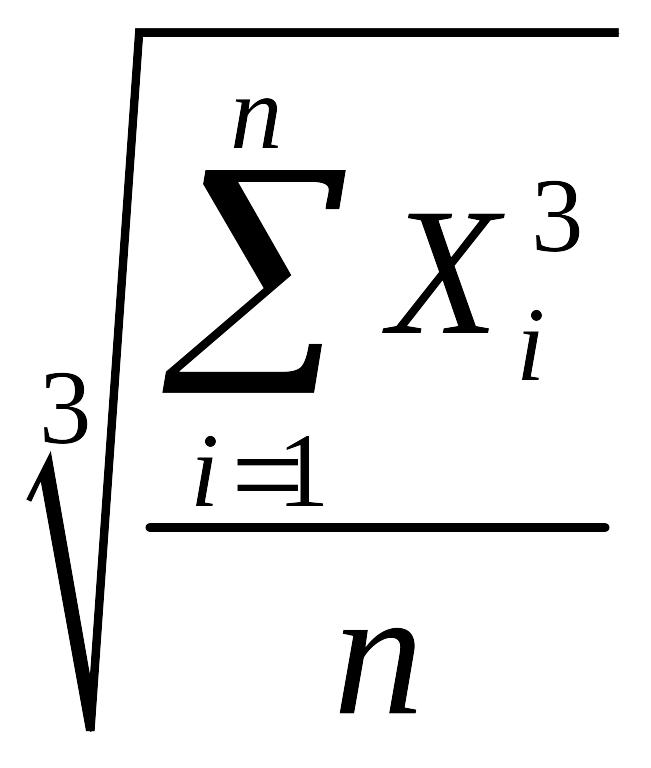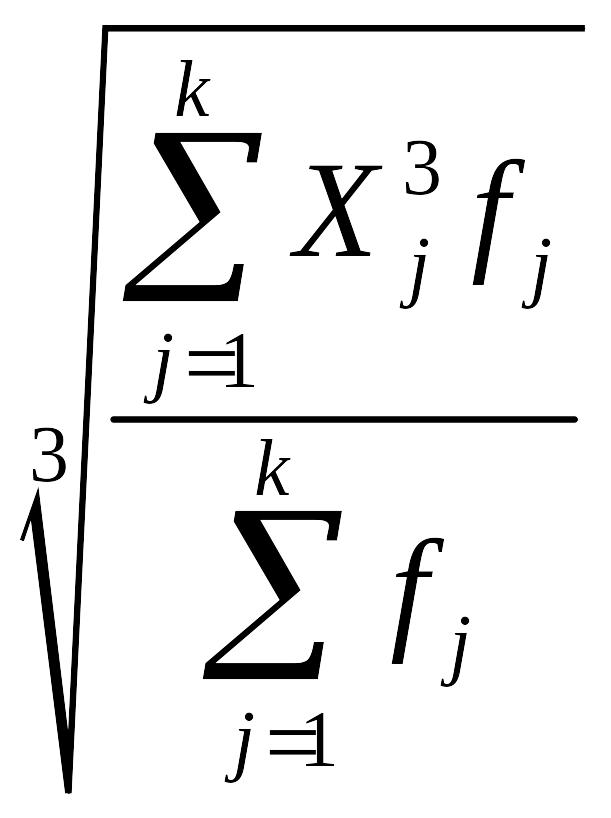Виды степенных средних

Вид степенной средней	Показа-тель степени ( )	Формула расчёта
		Простая	Взвешенная
Гармоническая	-1
Геометрическая	0
Арифметическая	1
Квадратическая	2
Кубическая	3

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.

Расчет средних по результатам группировки

Очень часто исходные данные для анализа бывают представлены в сгруппированном виде, когда для каждого значения усредняемого признака Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических или гармонических). Сложности возникают, когда в сгруппированных данных указывается не конкретное значение признака Х по каждой группе, а лишь интервал его изменения. В данном случае правильный расчет общей средней величины возможен, если удается получить среднее значение признака по каждой группе. Если же это сделать невозможно, то их заменяют серединами интервалов. Таким образом, расчет средней арифметической делают по формуле

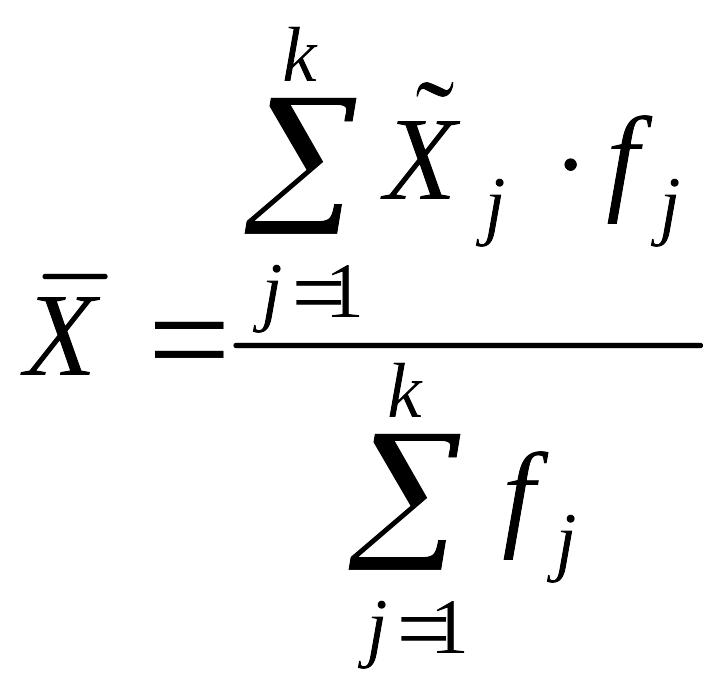, где .

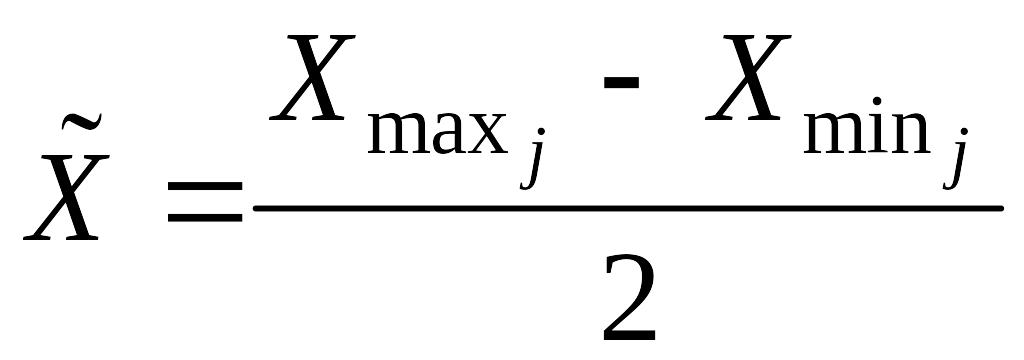Отметим, что расчет среднего значения по данным группировки требует особого внимания при выборе взвешивающего показателя.

Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:

1. Величина средней арифметической не изменится, если веса всех вариантов умножить или разлить на одно и то же число.

2. Если все индивидуальные значения признака (все варианты) увеличить или уменьшить в одно и то же число раз, то среднее значение получившегося нового признака будет во столько же раз отличаться от среднего значения исходного показателя.

Структурные средние

Структурные средние применяются для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся данным ее расчет не может быть выполнен.

В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака, и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Рассмотрим случай, когда значения признака Х представлены в виде интервальных рядов. Поскольку медианное значение делит всю совокупность на две равные части, оно оказывается в одном из интервалов признака Х. С помощью интерполяции в этом медианном интервале, находят значение медианы:

,

где Х_Me – верхняя граница предмедианного интервала (начало медианного);

h_Me – величина медианного интервала;

- половина от общего числа наблюдений.

- сумма наблюдений, накопленная до начала медианного интервала;

- число наблюдений в медианном интервале.

Вспомогательными описательными характеристиками распределения варьирующего признака являются структурные средние мода и медиана.

Мода - это варианта, наиболее часто встречающаяся в вариационном ряду. Если ряд дискретный, то модой будет варианта, у которой максимальная частота.

Мода для интервального ряда:

;

где Xm_o- это нижняя граница модального интервала;

h - величина модального интервала;

fm_o - частота модального интеграла;

fm_o-1 - частота интервала, предшествующему модальному;

fm_o+1 - частота интервала, последующего за модальным;

Модальный интервал определяется по наибольшей частоте.

Медиана – это середина вариационного ряда (делит вариационный ряд пополам).

В дискретном ряду^; медиане соответствует та варианта, у которой первая накопленная частота больше половины объема совокупности. Для интервального ряда медиана рассчитывается так:

;

где Xm_e - нижняя граница медианного интервала;

h - величина интервала;

Σ f/2 - половина объема совокупности;

Sm_e-1 - это накопленная частота до интервала, предшествующего медианному;

fm_e - частота медианного интервала.

Медианный интервал определяют по накопленным частотам. Медианному интервалу соответствует первая накопленная частота, которая больше половины объема совокупности.

Для определения уровня колеблемости признака в совокупности применяются показатели вариации. Они бывают:

1. Размах вариации - это наиболее грубый показатель вариации:

где X max и X min - соответственно наибольшее и наименьшее значение варианты.

Выражается он в тех же единицах, что и варианта.

2. Среднее линейное отклонение:

а) простое:

;

б) средневзвешенное:

;

Этот показатель более обоснован, чем R, так как он не зависит от случайных колебаний вариант и учитывает всю сумму отклонений вариант от их среднего значения.

Наиболее применяемыми показателями в статистике в качестве меры колеблемости являются дисперсия - Д (δ²) и среднеквадратическое отклонение (δ).

3. Дисперсия бывает:

а) простая:

;

б) взвешенная:

;

4. Среднеквадратическое отклонение:

а) простое:

;

б) взвешенное:

;

5. Коэффициент вариации является относительным показателем вариации:

Его применяю: для сравнения уровня колеблемости или уровня однородности двух совокупностей, у которых варианты выражены в различных единицах измерения. Кроме того, коэффициент вариации применяется для оценки степени надежности средней. Если V≥30%, средняя считается ненадежной для данной совокупности и эту совокупность необходимо разбивать на однородные группы и для каждой группы рассчитывать свою среднюю.

Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции.

Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.

Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.