Тема 2. Абсолютные и относительные величины

Абсолютная статистическая величина характеризует размер или объем явлений. Существует 2 метода получения абсолютных статистических величин:

1) в результате статистического наблюдения:

2) путем расчетов.

Единицы измерения абсолютных статистических величин бывают:

а) натуральные;

б) стоимостные (денежные);

в) условно-натуральные:

г) трудовые измерители.

Условно-натуральные единицы измерения используются для определения размера разнокачественной продукции, но обладающей одной потребительной стоимостью (теплотворная способность топлива в килокалориях, мощность машин, тракторов в лошадиных силах).

Абсолютные статистические величины бывают двух видов:

а) характеризуют численность совокупности (численность работающих на предприятии);

б) характеризуют объем явлений, т.е. объем признаков, присущих единицам совокупности.

Относительной величиной называется показатель, который характеризует количественное соотношение двух или нескольких абсолютных статистических показателей. По содержанию сравниваемых показателей относительные величины бывают одноименные и разноименные

Одноименные получаются в результате сравнения показателей одинакового содержания. Наиболее применяемыми формами выражения этих относительных величин являются коэффициенты, проценты и промили. Гот показатель, с которым сравнивают, называют базой сравнения. Если за базу сравнения принята единица - получают коэффициент, если 100 – процент (%), если 1000 — промилю (⁰/₀₀). если 1000 – децепромилю (⁰/₀₀₀).

Разноименные относительные величины выражаются в единицах измерения сравниваемых показателей.

Все относительные показатели бывают 8 видов:

1. Относительная величина выполнения плана q вып. плана (программы, задания):

;

где Q_фактич.— фактический уровень показателя;

Q_план – плановое задание.

2. Относительная величина планового задания. Характеризует, на сколько процентов предусмотрен рост или снижение плана данного показателя, но сравнению с фактически достигнутым уровнем в предыдущем периоде:

;

где Q_базисн – фактически достигнутый уровень в предыдущем периоде

3. Относительная величина динамики (или темп роста). Характеризует изменение явлений во времени. Выражается в процентах или коэффициентах:

;

Между этими тремя видами относительных величин существует такая взаимосвязь.

(1);

4 Относительная величина структуры. Она характеризует долю или удельный вес в целом (например, удельный вес мужчин среди населения). Выражается в коэффициентах или %.

5 Относительная величина координации Характеризует соотношение частей одного целого между собой (например, отношение числа женщин к числу мужчин: 117:110).

6. Относительная величина сравнения. Характеризует соотношение размеров изучаемых совокупностей.

Названные 6 видов относительных величия являются одноименными относительными величинами.

Разноименные относительные величины.

7. Относительная величина уровня экономического развития характеризует размер социально-экономических показателей в расчете на душу населения (например, производство и потребление важнейших продуктов питания на душу населения).

8 Относительная величина интенсивности. Она характеризует степень распространенности одного явления в другом, или как часто данное явление встречается в определенной среде (например, частота дорожно-транспортных происшествий).

СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ

Средняя величина - это обобщающая или типическая характеристика совокупности по одному количественному признаку, которая характеризует уровень этого признака, отнесенный к единице совокупности. Получают средние величины путем деления объема признаков, взятого по всей совокупности, на число единиц, обладающих данным признаком:

;

В значении средней улавливаются общие черты закономерности массовых общественных явлений.

Научная методология расчета средних :

1. Средняя должна рассчитываться по качественно однородной совокупности, поэтому расчет средней тесно связан с методом группировок. Для выделения качественно однородной совокупности вначале проводят типологическую группировку, а затем по каждой группе рассчитывают среднюю.

2. Средняя рассчитывается только при массовом обобщении единиц совокупности (связано с законом больших чисел).

Общая формула для расчета средних: ;

В зависимости от m средние бывают таких видов:

а) средняя арифметическая (m = 1);

б) средняя гармоническая (m = -1);

в) средняя квадратическая (m = 2);

г) средняя геометрическая (m = 0).

д) средняя хронологическая.

Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя. Выбор формы средней всегда однозначен.

Обычно затруднения вызывает выбор 2-х форм средних: а) и б).

Средняя арифметическая а) бывает 2-х видов:

1. простая ;

Если варианта встречается один или одинаковое число раз, то применяемся средняя арифметическая простая.

2) средне - арифметическая взвешенная: ;

где f - частота появления каждой варианты.

Средняя арифметическая взвешенная применяется в том случае, если есть варианта и частота появления этой варианты.

Средняя гармоническая б) бывает двух видов:

1) простая ;

2) взвешенная ;

где М – объем явления. Средняя гармоническая применяется в том случае, если не указана по условию задачи частота появления признака, а дан объем явлений.

Если в исходной схеме расчета по условию задачи известен знаменатель, применяется средняя арифметическая взвешенная, а если в схеме расчета известен числитель, то применяется средне гармоническая взвешенная.

Средне квадратическая в) бывает двух видов:

1) простая ;

2) взвешенная ;

Среднеквадратическая применяется в том случае, когда в качестве варианты выступают не абсолютные значения признака, а их отклонения or нормы или от заданной величины.

Средние величины делятся на два больших класса:

1. Степенные средние; к ним относятся такие наиболее известные и часто применяемые виды как средняя геометрическая, средняя арифметическая и средняя квадратическая;

2. Структурные средние, в качестве которых рассматриваются мода и медиана.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по негруппированным данным и имеет следующий общий вид:

,

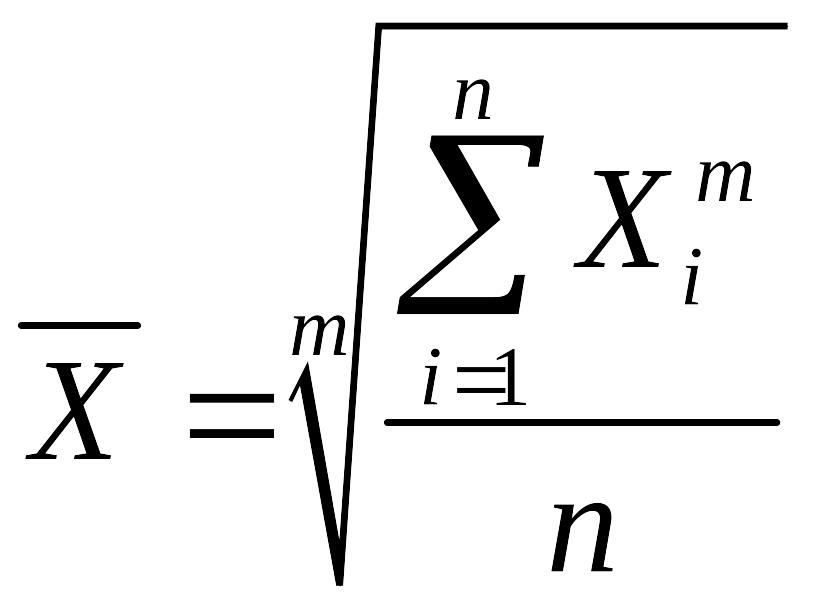где – значение осредняемого признака;

– показатель степени средней;

– объем выборки.

Взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:

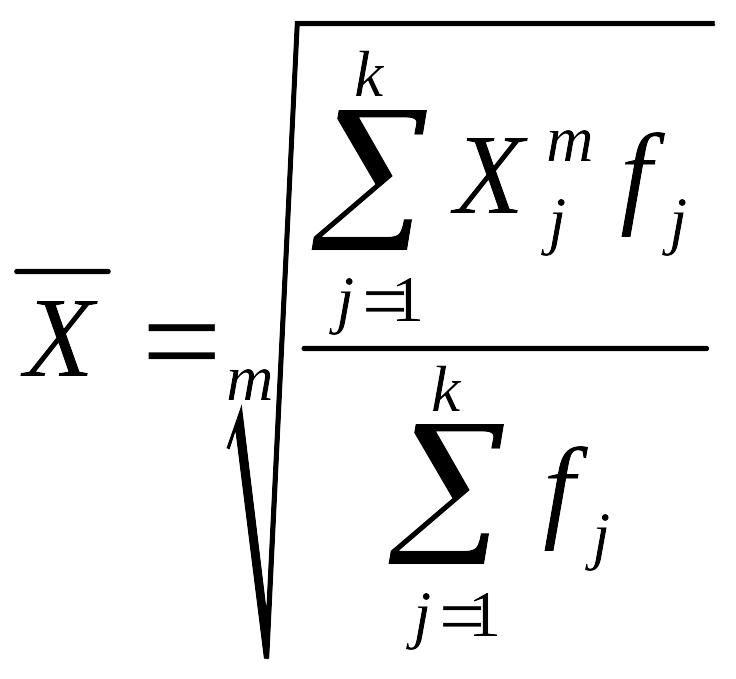
где – значение осредняемого признака или серединное значение интервала, в котором измеряется варианта;

– количество значений признака или количество интервалов группирования;

– показатель степени средней;

– частота, показывающая, сколько раз встречаются -е значения осредняемого признака.

Общие формулы расчёта степенных средних имеют показатель степени ( ). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних, представленных в таблице.