Лабораторна робота № 3 Вибірки і їх подання

МЕТА І ЗАДАЧІ

Метою роботи, яка виконується, є ознайомлення студентів з вибірками та одержання практичних навиків по найбільш поширеним методам їх обробки з використанням сучасної обчислювальної техніки.

ОСНОВНI ТЕОРЕТИЧНI ПОЛОЖЕННЯ

Нагадаємо, що таке вибірка, варіаційний ряд, емпіричний розподіл, групування, гістограма, вибіркові характеристики тощо.

Вибіркою х₁, ..., х_n об’єму n із сукупності, розподіленої по F(х), називається n незалежних спостережень над випадковою величиною  з функцією розподілу F(x).

Варіаціним рядом х₍₁₎ х₍₂₎ ...  х_(n) називається вибірка, записана в порядку зростання її елементів.

Кожному спостереженню з вибірки привласнимо ймовірність, рівну 1/n; отримаємо розподіл, що називають емпіричним; йому відповідає функція емпіричного розподілу

 = ,

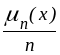де _n(х) - число членів вибірки, менших х. Значення цієї функції для статистики визначаються тим, що при n  

 F(x) (теорема Гливенко).

Вибірки великих об’ємів важко відслідковувати; розіб’ємо діапазон значень вибірки на рівні інтервали і підрахуємо для кожного інтервалу частоту- кількість спостережень, потрапивших у нього; відношеня частоти, до загального числа спостережень n, називають відносними частотами; графічне подання розподілу частот по інтервалах  гістограмою; накопиченої частоти для даного інтервалу називають суму частот даного інтервалу і всіх тих, що лівіше нього.

Числові характеристики емпіричного розподілу називаються вибірковими характеристиками: вибіркові середні (математичне очікування), дисперсія:

= , s²=

вибірковий момент порядку к:

m_k = ;

вибіркові квантилі _p порядку р - корені рівняння

F(_p)=p,

якими являються члени варіаційного ряду

_(p)=_([np]+1),

де [nр] означає цілу частину nр; окремим випадком (p = 0.5) є вибіркова медіана - центральний член варіаційного ряду. Значення вибіркових характеристик полягає в тому, що при n   вони прямують до істинних значень розподілу F(х).

Наведемо приклади виконання з допомогою пакету STATISTICA. Вихідні дані наведені в табл.1. E(a) в таблиці означає показовий (експоненціальний) розподіл з математичним очікуванням, рівним a).

таблиця 3.1

¹	Закон	n		¹	Закон	n	
1	R [0, 2]	50	0.03	14	N (1,4)	60	0.01
2	N(2, 0.25)	60	0.02	15	E (5)	70	0.03
3	E (3)	70	0.01	16	R [0.3]	80	0.1
4	R [1, 3]	80	0.02	17	N (1,4)	50	0.3
5	N (1, 1)	50	0.01	18	E (1)	60	0.2
6	E (2)	60	0.03	19	R [1,3]	70	0.03
7	R [2, 3]	70	0.01	20	N (1,1)	80	0.02
8	N (0, 4)	80	0.03	21	E (2)	50	0.01
9	E (3)	50	0.02	22	R [2,3]	60	0.02
10	R [0, 2]	60	0.03	23	N (2,1)	70	0.01
11	N [2, 1]	70	0.02	24	E (3)	80	0.03
12	E (4)	80	0.01	25	R [1,2]	50	0.01

ПОСЛІДОВНІСТЬ ВИКОНАННЯ РОБОТИ

Під час виконання роботи необхідно:

• згенерувати вихідні вибірки;

• побудувати варіаційний ряд;

• побудувати графіки функцій емпіричних розподілів;

• побудувати гістограми вихідних вибірок;

• визначити основні вибіркові характеристики;

• перевірити гіпотези про тип розподілу;

• побудувати діаграму розсіювання та обчислити кореляційну матрицю двовимірної вибірки;

• побудувати діаграму розсіювання трьохвимірної вибірки.

Генерація вибірки

Згенеруємо, наприклад, вибірку об’єму n =50 показовим розподілом із середнім значенням 5.

Створимо новий файл:

File - New Data - вкажемо ім’я файлу у вікні File Name : descript (наприклад) - OK. На екрані сітка-таблиця; в її заголовку вказані назви і розміри : 10v * 10c - ( 10 змінних ( variables ) - стовпчиків по 10 спостережень ( cases ) - рядків.

Перетворимо таблицю до розмірів 150:

кнопка Vars (на екрані) - Delete; вікно Delete Variables: вкажемо які змінні - стовпчики забрати : From variable : var 2, To variable : var 10 - OK - Кнопка Cases - Add ( додовання ) - вікно Add Cases: вкажемо, скільки рядочків добавити і куда : Number of Cases to Add : 40, Insert after Case : 1 ( наприклад ) - OK.

Згенеруємо вибірку:

виділимо стовпчик - змінну Var1 ( кліком мишки по її заголовку) - нажимаємо праву клавішу – у відкрившомуся меню вибираємо Variable specs ( специфікації змінної ) - в появившомуся вікні Variable 1 введемо Name x ( наприклад ), в нижньому полі Long name вводиться вираз, що означає змінну. Ввід можна зробити набором на клавіатурі чи з допомогою клавіші Functions, вибираючи в меню Kategory і Name потрібну функцію і вставляючи клавішою Insert. Для задання закону розподілу слід ввести, наприклад,

=rnd(2) для R[0, 2],

=Vnormal(rnd(1); 2; 0.5 ) для N(2, ²=0.5²),

=VExpon(rnd(1); 0.2 ) для E(5) з среднім 1/0.2=5; (для нашого прикладу замість значення параметру =0.2 можна набрати вираз 1/5).

Така форма задання визначається способом генерації: з допомогою функції, оберненої (буква V) до функції розподілу і генератора випадкових чисел R[0, 1] ( rnd(1)).

Роздрукуємо вибірку командою Print меню File.

Подивимося вибірку графічно:

Graphs - Custom Graphs (налаштування графіків) - 2D graphs – у відкритому вікні все можна залишити по замовчуванню - .OK. Спостережуваний графік (рис.3.1) роздруковуємо.

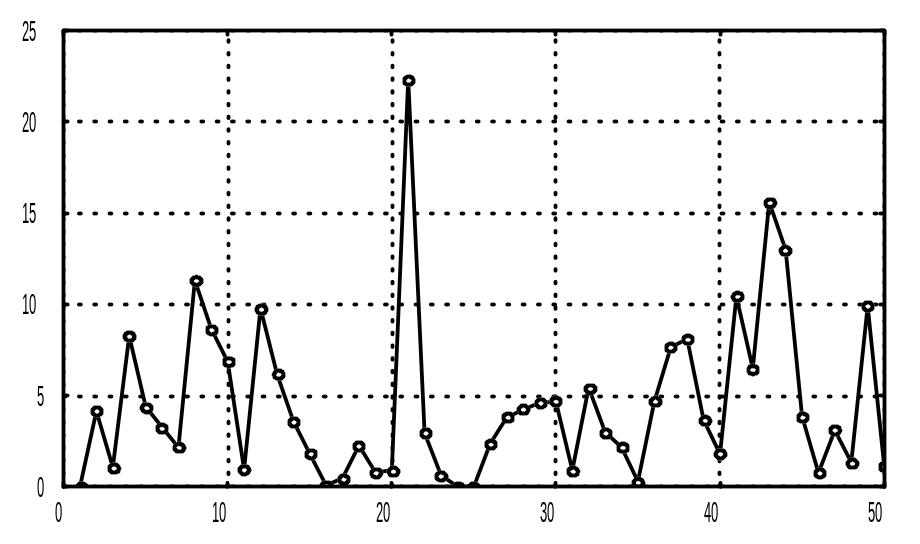
Рисунок 3.1 – Спостереження, розподілені по показовому закону з среднім 5 (n = 50).

Побудова варіаційнного ряду

Перший спосіб:

виділимо потрібну змінну (стовпчик) - натиснемо праву клавішу мишки - виберемо Quiq Stats Graphs (швидкі статистики і графіки) - Values / Stats of Vars (значення і статистики ) - спостерігаємо варіаційний ряд і вибіркове среднє (mean) і стандартне відхилення ( SD ).

Другий спосіб:

ввійдемо в модуль Data Menagement (подвійний клік лівою клавішою мишки на чистому полі і вибір модуля у вікні Module Switcher; якщо модуль уже завантажений, то Alt+Tab до появи модуля) - Analysis Sort - встановлюємо ім’я змінної, тип сортування: Ascen (по зростанню ) чи Desc ( по спаданню) - OK.

Функція емпіричного розподілу

Перший спосіб:

Graphs - Stats 2D Graphs - Histogram - у з’явившомуся вікні встановимо: Graph Type : Regular, Cumulative Counts (накопичені частоти), Fit Type (підбираючий тип) : Exponential (для нашого прикладу) чи off (без підбору), Variablles: x, Categories (число інтервілів групування) : 250 - OK.

Спостерігаємо графік функції емпіричного розподілу (рис. 3.2). Графік можна відредагувати: змінити лінії, точки, фон, шкали, підписи; для цього необхідно підвести стрілку в потрібне місце і двічі клікнути лівою клавішою мишки. Виводимо його на друк чи зберігаємо.

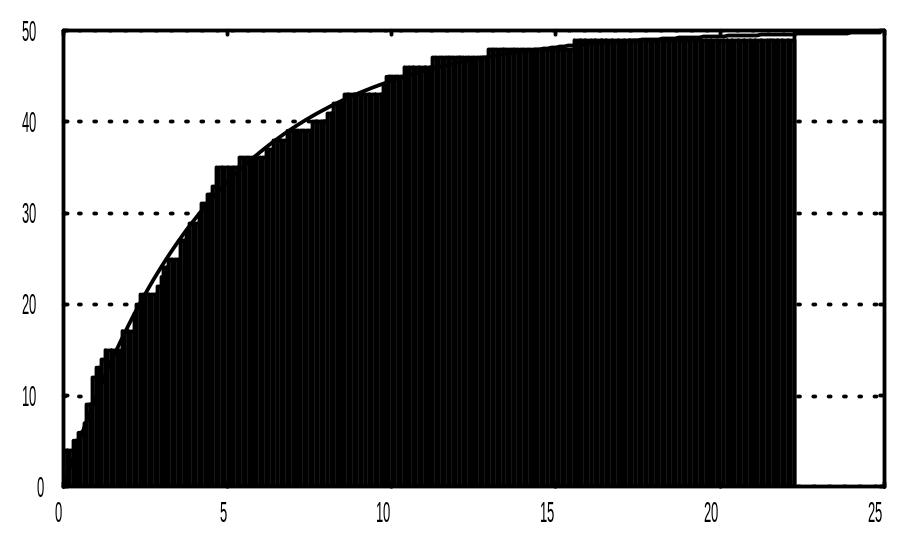
Рисунок 3.2 – Функція емпіричного розподілу

Другий спосіб :

упорядкуємо за зростанням нашу вибірку (див. Побудова варіаціоного ряду);

створимо нову змінну F для значень функції:

клавіша Var - Add - ... ( див. Генерація вибірки) - виділимо нову змінну NEWVAR - права клавіша мишки - Variable Specs ... - Name: F - Long name: = V0/50

(оператор V0 створює масив цілих чисел) ; побудуємо графік:

Graphs - Custom Graphs - 2D Graph - в новому вікні установимо: в полі X: x, в полі Y: F, Step Plot (сходинки, але не Line Plot - лінії) - OK.

Спостерігаємо функцію емпіричного розподілу (з точністю до дрібного групування з 250 інтервалами).

Групування даних

Analysis Frequency Tables - у вікні Frequency Tables задамо No of exact intervals: 10 (10 інтервалів групування; чи Step size: 2, starting at: 0), в полі Display options відмітимо Cumulative frequences ( накопичені частоти ), Percentages (проценти - відносні частоти), Cumulative Percentages (накопичені частоти ) - OK.

Спостерігаємо таблицю групованих даних. Виводимо її на друк і зберігаємо.

Побудова гістограми частот

Graphs - Stats 2D Graphs - Histograms - в появившомуся вікні встановлюємо: ім’я змінної, Graph Type: Regular, Fit Type; off ( без підбору ) чи потрібний тип, число інтервалів групування Categories: чи Auto (автоматичний вибір числа інтервалів) - OK.

Спостерігаємо гістограму (рис. 3.3). Відредагуємо графік, якщо необхідно. Виводимо на друк і зберігаємо.

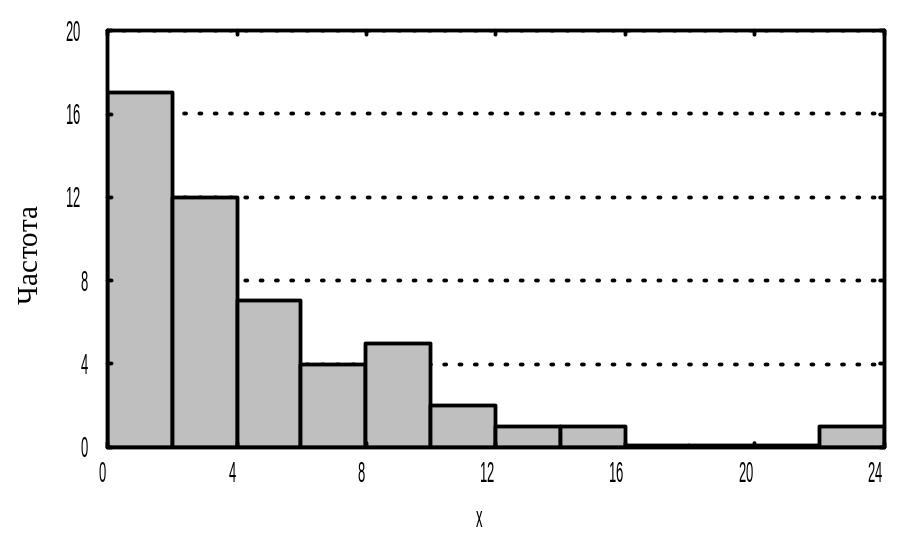
Рисунок 3.3 – Гістограма.

Вибіркові характеристики

перший спосіб: на заголовку стовчика з вибіркою клікнемо правою клавішою мишки - Quick Basic Stats... - Descriptives of var - отримоємо таблицю з характеристиками: mean (среднє), Confid 95% ( довірчі інтервали нижній і верхній з рівнем довіри 0.95 ), Sum ( сума ), Minimum, Maximum, Range ( розмах ), Variance ( дисперсія ), Std. Dev. ( стандартне відхилення ) тощо. Порівняємо вибіркове среднє, медіану і стандартне відхилення з відповідними теоретичними значеннями. Це ж, також можна зробити через меню: Anflisis - Quick Basic Stats ...

Другий спосіб : на заголовку стовчика з вибіркою клікнемо правою клавішою мишки - Block Stats / Columns (блок статистик по колонках ) - виділимо необходідне або All.

Опис двомірних вибірок

Ввід даних: задамо нову таблицю 232, назвемо стовпчики X і Y. Заповнимо таблицю вручну заданими в табл.2 значеннями.

Діаграма розсіювання:

Graphs - Stats 2D Graphs... - Scatterplots... - вводимо значення по осях X і Y (натиснувши на кнопку Variables і вибравши змінні ) - OK.

Роздрукуємо діаграму (рис. 3.4) або збережемо.

Вибіркові характеристики.

Виділимо ті змінні, по яких потрібно вибіркові характеристики - клікнемо правою клавішою мишки - Quick Basic Stats - Descriptivs of VARS... Спостерігаємо таблицю вибіркових характеристик (тих же, що инше). Віддрукуємо таблицю чи збережемо.

Вибіркові характеристики можна внести в таблицю даних, в кінець відповідних стовпчиків. Виділимо потрібні стовпчики, дальше див. другу частину п. Вибіркові характеристики..

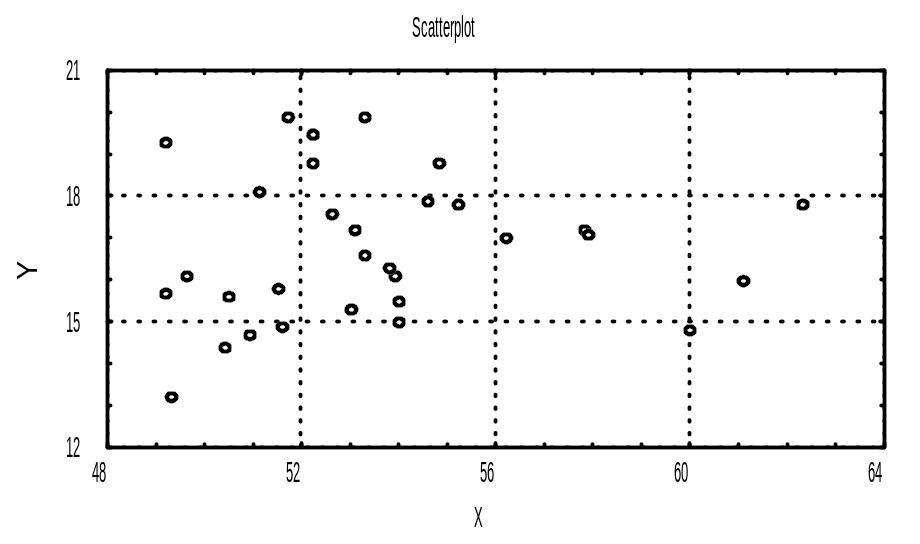
Рисунок 3.4 – Діаграма розсіювання

Визначимо кореляційну матрицю:

Analysis - Correlation matrices - Two lists - First list: All - Second list: All - OK - Cancel (відміна пропозиції на нову матрицю).

Матрицю віддруковуємо чи зберігаємо.

двомірна гістограма (рис. 6).

Graphs - Stat 3D Sequential Graphs - Bivariate Gistogram - встановимо по осях X і Y потрібні змінні ( кнопкою Variables), задамо число інтервалів по кажній осі - OK.

Роздрукуємо гістограму.

ОФОРМЛЕННЯ ЗВІТУ

Звіт про виконану роботу повинен містити пояснювальну записку із розрахунками та графіками, а також аналіз результатів розрахунку.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Що таке вибірки?

2. Що таке варіаційний ряд?

3. Дайте визначення медіані.

4. Наведіть вибіркові характеристики.