17) Коэффициент деформации
Отношение размеров тела после деформации к соответствующим начальным размерам тела называется коэффициент деформации.
-
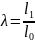Коэффициент вытяжки
коэффициент
уширения
-
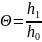коэффициент осадки
Условие постоянства объема через эти коэффициенты:
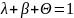
18) Понятие упругости. Закон Гука для упругих деформаций.
Упругость – свойство материала сохранять свою форму и размеры, т.е. материал деформируется
Закон Гука
Сила упругости возникающая в теле при его деформации прямо пропорционально этой деформации.
F=K∆l
K-коэффициент упругости; l-длинна
K=ES/l
E-модуль Юнга; S-площадь поперечного сечения
ε=∆l/l
σ=F/S; σ=E∙ε
Закон Гука справедлив только для малых напряжений.
19) Обобщённый закон Гука.
Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного, и как частый случай, плоского напряженных состояний. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил.
П
усть
задано произвольное объемное напряженное
состояние с главными напряжениями
Ϭ1,Ϭ2,Ϭ3.Представим его в виде суммы трех
линейных напряженных состояний.
Учитывая, что при линейном напряженном
состоянии
Д
еформации
в направлении действия главных напряжений
равны
Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации e1, e2, e3, в направлении главных напряжений называются главными деформациями.
С
оотношения
обобщенного закона Гука могут быть
записаны для любых площадок, но т.к. при
этом будут действовать, кроме нормальных
и касательные напряжения , то необходимо
добавить три соотношения для вычисления
угловых деформаций. Таким образом, для
произвольных площадок обобщенный закон
Гука содержит 6 соотношений, связывающих
деформации и напряжения:
20) Уравнение, связывающее напряжение и деформации.
Напряжения и деформации упругой среды связываются законом гука. Закон гука-Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь 
—
сила, которой растягивают (сжимают)
стержень, 
—
абсолютное удлинение (сжатие) стержня,
а 
— коэффициент
упругости (или
жёсткости).
Коэффициент
упругости зависит как от свойств
материала, так и от размеров стержня.
Можно выделить зависимость от размеров
стержня (площади поперечного сечения 
и
длины 
)
явно, записав коэффициент упругости
как
В
еличина 
называется модулем
упругости первого рода или модулем
Юнга и
является механической характеристикой
материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
21. На диаграмме растяжения выделяют следующие участки:
ОА - участок пропорциональности.
ОВ - участок упругости.
ВС - участок текучести.
СД - участок упрочнения.
ДК - участок образования шейки.
Предел пропорциональности-это максимальное напряжение до которого выполняется закон Гука. Предел упругости - это напряжение, до которого действуют упругие деформации. Предел текучести - это напряжение, которое отвечает нижнему положению площадки текучести, после него начинается пластическая деформация. Предел прочности – это напряжение, которое отвечает наибольшей нагрузки предшествующие разрушению образца.
22. Гипотеза Мизеса-Губера. Любая эл. частица металлического тела переходит из упругого состояния в пластическое, когда интенсивность напряжений достигает величины равной напряжению текучести. При линейном пластичном состоянии - интенсивность напряжения при пластической деформации.
+
+
)
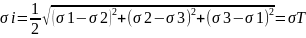
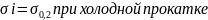
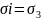
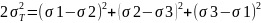
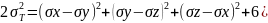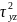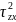Сумма кв. разности главн. Напряжений, есть величина постоянная и равная удвоен. квадрату напряжения текучести.
23. Гипотеза Cен-Венана: пластическая деформация наступает тогда, когда одно из главных касательных напряжений достигнет половины предела текучести независимо от схемы напряжённого состояния.
;
;
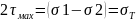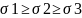
Параметр
Лоде был установлен экспериментально.
Однако, его можно выделить и аналитически: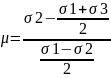
.
Он характеризует напряжённое состояние
в точке.
25. О пластичности и сопротивлению деформации можно говорить по схемам главных напряжений. Сопротивление деформации максимально при деформации по одноименным схемам главных напряжений и сопротивление деформации уменьшается при разноименных схемах деформации. При среднем нормальном напряжении напряженное состояние будет чисто девиантным. При наложении на девиаторы + шарового тензора т.е. всестороннего равномерного растяжения пластичность падает в тем большей степени, тем больше величина компонента шарового тензора и наоборот при наложении на девиаторы – шарового тензора т.е. всестороннего зжатия, пластичность увеличивается в тем большей степени тем больше величина компонента шарового тензора.
О том какой происходит процесс ОМД нельзя судить только по схеме гл. напряжений или только по схеме гл. деформаций. Необходимо использовать их совокупность ( механические схемы деформаций)
Мех. Схемы деформаций дает граф. Представление о наличии и знака гл. напряжений и гл. деформаций. Они отображают схему действия сил и определяют характер деформаций.
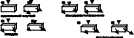
Существует 3 вида схем девиатора= схеме гл. деформаций
Характеры девиаторов
2 вид схем
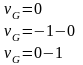1 вид схем
3 вид схем
Главные средние напряжения
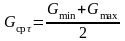2 вид
1 вид
3 вид