13) Тензор деформаций. Его составляющие.

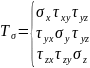
Тензор напряжений-это функция определяющая напряжение для любой площадки, проходящей через данную точку

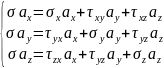
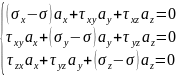
=0

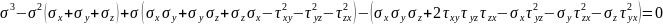
Тензор напряжений имеет 3 инварианта. 1-линейный 2-квадратичный 3-кубический 3-кубический

14) Понятие об инвариантах тензора деформаций.

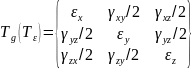
Деформированное Состояние в точке = тензору деформации с компонентами линейные и угловые деформации.

-тензор при главных напряжениях

Шаровой тензор деф-ции(изменение объема)

Девиатор: изменение формы)

3инварианта: линейный,квадратичный и кубический.

Линейный Квадратичный кубический: 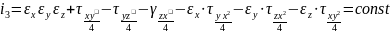Схема главных деформаций

Существует 3 вида схем главных деф-ций. 1) схемы у которых 1 главная деф-ция положительная, а 2 другие отриц.(растяжение). 2) одна главная деф-ция равна 0,а две др. равны по абсолютной велечине но разные по знаку.(плоское сост.-сдвиг) 3)1отриц а 2ост. Положительные(сжатие)

1и 3 виды-объемные схемы.

Простое растяжение- 2 отриц. Деф-ции равны.

Простое сжатие – 2 положит. Деф-ции равны.

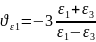
-1 ви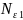д < <1 – 3 вид

15) Схема деформаций. Виды и количество схем.

Существуют 3 схемы главных деформаций: две объемные (растяжение-растяжение-сжатие(1) и растяжение-сжатие-сжатие(3)) и одна плоская (растяжение-сжатие(2), по третьей оси деформации нет). Из закона постоянства объема следует, что все главные деформации не могу быть одного знака, т.е. растяжение или сжатие не может быть по всем осям осям одновременно.

16) Абсолютные, относительная и логарифмическая деформации. Свойство аддитивности.

Абсолютные деформации:

по толщине – обжатие   ;

по длине – удлинение   ;   измеряются в единицах длины

по ширине – уширение  ;

Абсолютные показатели неполно характеризуют величину деформации, так как не учитывают размеры деформируемого тела, а учитывают только их изменение. Обладают свойством адитивности.

 

О тносительные деформации отношение абсолютных деформаций к соответствующим исходным размерам.

по толщине – относительное обжатие  ;

п о длине – относительное удлинение ;

по ширине – относительное уширение  .

 

Относительные деформации измеряются либо в долях единицы, либо в процентах. Не обладают адитивностью.

Истинные (логарифмические)

Таким образом, истинные деформации представляют собой натуральный логарифм отношений размеров после деформации и до нее:

по толщине - ;     по ширине -  ;   по длине -  .

Если «+» то растяжение ,если «-» то сжатие.

К оэффициенты деформации – отношение размеров тела после деформации к соответствующим размерам до деформации.

Коэффициент деформации по толщине – коэффициент обжатия ;

К оэффициент деформации по длине – коэффициент удлинения ;

Коэффициент деформации по ширине – коэффициент уширения .

Аддитивность – свойство суммировать деформации.