Связь между дифференцируемостью и непрерывностью функции

Рассмотрим следующие вопросы, который касаются функций.

Если функция непрерывна, то она дифференцируема?

Если функция дифференцируема, то она непрерывна?

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции   . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

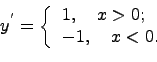
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:

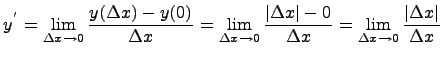
данный предел равен 1, если   и равен (-1), если   , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема. 

Производные функций вычисляются с применением следующих теорем:

 

ТЕОРЕМА 1. Производная от константы равна нулю.

ТЕОРЕМА 2. Константу можно вынести за знак производной, то есть

ТЕОРЕМА 3. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:

ТЕОРЕМА 4. Производная произведения двух функций равна

ТЕОРЕМА 5. Производная частного двух функций равна

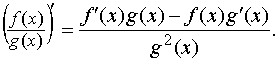
ТЕОРЕМА 6 – теорема о вычислении сложной функции. Пусть y=F(u), где u=(x), тогда

Неявно заданная функция

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

Производные высших порядков явно заданной функции

Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.

Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у"

Итак, у"=(у')'.

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'

Производной n-го порядка (или n-й производной) называется производная от производной  (n-1) порядка:

y⁽ⁿ⁾=(y^(n-1)) .

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у^ν или у⁽⁵⁾— производная пятого порядка).

Производные высших порядков неявно заданной функции

Пусть функция у=ƒ(х) задана неявно в виде уравнения F(x;y)=0.

Продифференцировав это уравнение по х и разрешив полученное уравнение относительно у', найдем производную первого порядка (первую производную). Продифференцировав по х первую производную, получим вторую производую от неявной функции. В нее войдут х,у,у . Подставляя уже найденное значение у' в выражение второй производной, выразим у" через х и у.

Аналогично поступаем для нахождения производной третьего (и дальше) порядка.

Производные высших порядков от функций, заданных параметрически

Пусть функция у=ƒ(х) задана параметрическими уравнениями

Как известно, первая производная у'х находится по формуле (23.1)

Найдем вторую производную от функции заданной параметрически. Из определения второй производной и равенства (23.1) следует, что

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.                                             (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх,                                              (24.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение

производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке  АМ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

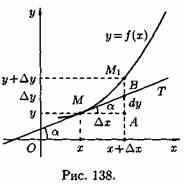
Основные теоремы о дифференциалах

Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.

Например, так как производная функции у=с равна нулю, то дифференциал постоянной величины равен нулю: dy=с'dx=0•dx=0.

Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

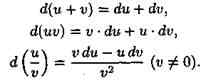
Докажем, например, вторую формулу. По определению дифференциала имеем:

d(uv)=(uv)'dx=(uv'+vu')dx=vu'dx+uv'dx=udv+vdu

Теорема 24.2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать

у'_х=у'_u•u'_x.

Умножив обе части этого равенства на dx, поучаем у'_хdx=у'_u•u'_хdx. Но у'_хdx=dy и u'_хdx=du. Следовательно, последнее равенство можно переписать так:

dy=у'_udu.

Сравнивая формулы dy=у'_х•dx и dy=у'_u•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.

Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.

Формула dy=у'_х•dx по внешнему виду совпадает с формулой dy=у'_u•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.

С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.

Например: d(cosu)=(cosu)'_udu=-sinu•du

Дифференциалы высших порядков

Пусть у=ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy=ƒ'(х)dx есть также функция х; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у=ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d²y или d²ƒ(х).

Итак, по определению d²y=d(dy). Найдем выражение второго дифференциала функции у=ƒ(х).

Так как dx=∆х не зависит от х, то при дифференцировании считаем dx постоянным:

d²y=d(dy)=d(f'(x)dx)=(ƒ'(х)dx)'•dx=f"(x)dx•dx=f"(x)(dx)² т. е.

d²y=ƒ"(х)dх².                                            (24.5)

Здесь dx² обозначает (dx)².

Аналогично определяется и находится дифференциал третьего порядка

d³y=d(d²y)=d(ƒ"(х)dx²)≈f'(x)(dx)³.

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: dⁿy=d(d^n-ly)=f⁽ⁿ⁾(x)(dx)ⁿ.

Отсюда находим, что , В частности, при n=1,2,3

соответственно получаем:

 

т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.