Сравнение бесконечно малых функций

     Для определения бесконечно малых и бесконечно больших функций воспользуемся, так называемым сравнением функций. Пусть у нас есть две функции p(x) и q(x), которые стремятся к А при аргументе x стремящемся к А. И будем рассматривать предел их отношения при аргументе x, стремящемся к некоторому числу A. Тогда возможны следующие варианты:

1)   , т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)).

2)   , т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)).

3) Если данный предел:   не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

4)  , т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)).

Эквивалентны бмф

Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.

Если    то α и ß называются эквивалентными бесконечно малыми (при х→x₀); это обозначается так: α~ß.

Например, sinx~х при х→0, т.к    при x→0, т. к. 

Теоремы о эквивалентных бмф.

1 . Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Теорема 18.2 . Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.

Действительно, так как

  т. е.    Отсюда     т. е. α~ß. Аналогично,   если  то α~ß.

Теорема 18.3 . Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Докажем теорему для двух функций. Пусть α→0, ß→0 при х→х_о, причем α — б.м.ф. высшего порядка, чем ß, т. е.   . Тогда

Следовательно, α+ß~ß при х→х₀.

Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.

Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.

Таблица эквивалентных бмф.

1. sinx~х при х→0;

2. tgx~х (х→0);

3. arcsinх ~ х (х→0);

4. arctgx~х (х→0);

5. 1-cosx~x²/2 (х→0);

6. е^х-1~х (х→0);

7. α^х-1~х*ln(a) (х→0);

8. ln(1+х)~х (х→0);

9. log_a(l+х)~х•log_aе (х→0);

10. (1+х)^k-1~k*х, k>0 (х→0);

Непрерывность функций.

Функция непрерывна в точке если в этой точке она определена и предел функции в этой точке равен значению функции в этой точке.

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Свойства непрерывных функций.

Теорема 1. Сумма непрерывных функций есть функция непрерывная.  Доказательство. Пусть функции     и     непрерывны в точке  a. Тогда

Согласно свойству пределов функций существование пределов функций     и     гарантирует существование предела их суммы. При этом

что и требовалось доказать.  Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.  Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная.  Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная.  Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.  Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.

Теорема 4. Любая элементарная функция непрерывна в области своего определения.  Для доказательства этой теоремы нужно показать, что для любого числа  a  из области определения элементарной функции     выполняется условие

Продемонстрируем справедливость теоремы на некоторых конкретных примерах.

1. Пусть 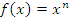  , где  n  – целое положительное число. Тогда

 

Первый член в правой части этого равенства представляет собой бесконечно малую функцию при  x → a  и, следовательно,

2. Покажем, что показательная функция 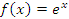   является непрерывной в каждой точке  a. Действительно,

   

Условия непрерывности.

1. Функция f (x) определена в точке x = a;

2. Предел 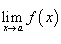  существует;

3. Выполняется равенство  .

4. Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

5. 

6. Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

7. Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Производные.

Произво́дная — определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

Из рис.1  видно, что для любых двух точек A и B графика функции:  

где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то    неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид: 

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +    точка перемещается на расстояние:  x ( t₀ +   )  x ( t₀ ) =  , а её средняя скорость равна:  v_a =    . При      0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

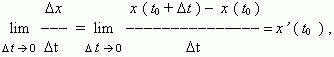
отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной.Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).