1.Основные понятия векторной алгебры.

1. Вектор – направленный отрезок с началом в т. А и концом в т. В. Или упорядоченная пара точек (А ;В)

2. Если начало и конец вектора совпадают то такой вектор называется еденичным.

3. Два вектора равны когда их длины и направления равны.

5. Два ненулевых вектора колинеарны если они лежат на одной прямой или паралельных прямых. Ноль вектор колинеарен любому вектору.

6. 3 ненулевых вектора называются компланарными если они лежат в одной или паралельных плоскостях. Их всегда можно поместить на 1 плоскость.

7. Угол между векторами – наименьший угол между направлениями векторов, но вектора выходят из общего начала. Если угол равен 90 то вектора – ортогональны.

2. Линейные операции над векторами.

1. Суммой любого конечного числа векторов есть отрезок соеденяющий начало первого с концом последнего, при условии что в-ра расположенны так что конец предидущего совпадает с началом последующего .

1. Правило паралелограма: суммой двух ненулевых векторов выходящей из одной точки есть третий вектор являющийся диагональю паралелограмма построенного на 2х данных векторах как на сторонах.

2. Правило Паралелепипеда: суммой 3х ненулевых векторов имеющих общее начало есть 4й вектор выходящей из того же начала и совпадающий с диагональю паралелепипеда построенного на векторах как на рёбрах.

2. Умножение векторов на скаляр. Произведением вектора А на число k есть вектор у которого: 1. Длина совпадёт с направлением вектора А если k>0 и противоположно если k <0.

Свойства:

1. (k1+ k2)*А=А* k1+А* k2.

2. k 1* k2*А= k1*( k2*А)= k2*( k1*А)

3. K*(А+В)= k*А+ k*А

4. Вычитание векторов

1. Разница 2х ненулевых векторов А и В выходящих из одного начала есть третий вектор С соединяющий конец вычитаемого с концом уменьшаемого.

СВОЙСТВА.

1. Любой ненулевой вектор можна выразить через орт.

2. 2 колинеарных вектора всегда можна выразить один через другой.

3. Если вектор R компланарен 2м неколинеарным векторам А и В, то: R=m*a+n*b. R – разложен по А и В. Любой ненулевой вектор можна еденичным способом разложить по 2м некомпланарным векторам в-ам.

5.Разложение вектора по ортам координатных осей.

1. Выделим на осях орты I j k, поместим в это пространство А, совместив начало вектора с началом координат. Найдём проэкции этого вектора на оси координат – для этого проведём через точку М или плоскости перпендикулярных осям ординаты. Обозначим точки пересечения М1 М2 М3 соответственно. Рассмотрим ОМ1, ОМ2, ОМ3.

ОМ1=|OM1|*i=a_x*i

OM2=|OM2|*j=a_y*j

OM3=|OM3|*k=a_z*k

Найдём сумму ОМ1+ОМ2+ОМ3=А.

А= a_x*i+a_y*j+a_z*k.

a_y a_x a_z – проекции вектора на оси соответственно.

Следствия:

1. Координаты орт. А совпадают с его направляющим косинусом. Направляющие косинусы: cosα= a_x/|A|, cosβ= a_y/|A|, cosγ= a_z/|A|

2. Для любоо вектора справедливо равенство cos² α+ cos² β+ cos² γ=1.

6. Действия над векторами:

 рассматриваются вектора и в пространстве.

6. Скалярное произведение векторов и его свойства

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

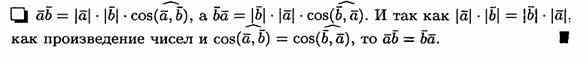
 Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а  b

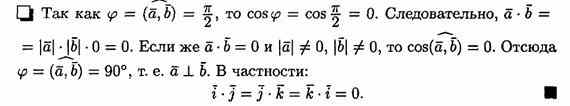
Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

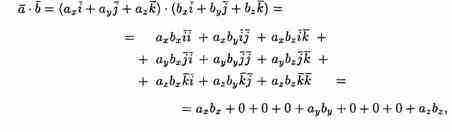
т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Приложения скалярного произведения

Угол между векторами

    Определение угла φ между ненулевыми векторами а = (a_x; a_y; a_z) и b=( b_х; b_у; b_г):

Отсюда следует условие перпендикулярности ненулевых векторов а и b:

Проекция вектора на заданное направление

Нахождение проекции вектора а на направление, заданное вектором b, может осуществляться по формуле

Выражение скалярного произведения через координаты.

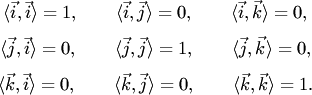
Векторное произведение

Вектор   называется векторным произведением неколлинеарных векторов   и  , если:

1) его длина равна произведению длин векторов   и   на синус угла между ними:   (рис.1.42);

2) вектор   ортогонален векторам   и  ;

3) векторы  ,  ,   (в указанном порядке) образуют правую тройку.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается  (или  ).

Свойства векторного произведения

Для любых векторов  ,  ,   и любого действительного числа  :

1

2

3

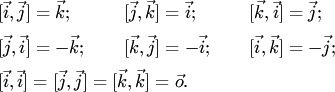
Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство "противоположно" закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

Выражение векторного произведения через координаты векторов

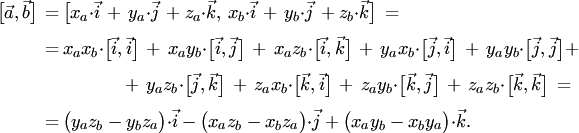
Запишем это равенство при помощи определителей второго порядка:

Правую часть можно представить как результат разложения символического определителя третьего порядка по первой строке

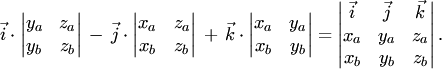
Приложение векторного произведения.

1. Установление колинеарности векторов. Если векторное произведение двух ненулевых векторов равно нулю то эти вектора колинеарны.

2. Нахождение площади паралелограмма и треугольника построенного на векторах как на сторонах. Площадь паралелограма равна векторному произведению. Площадь треугольника равна половине площади паралелограма.

3. Нахождение момента силы. Момент силы приложенной к точке А относительно точки О равен:

М=ОА*F.