248. Есептеңіз: .
$$0
249.
Интегралды
есептеңіз:
$$
250. Гиперболалық котангенс :
$$
251.Анықталу
облысы Е және мәндер облысы D
болатын
функциясы
функциясының
.... функциясы деп аталады,
егер
және
.
$$ кері
252.
Егер
функциясының
нүктесіндегі
өсімшесін :
( мұнда
-
сан,
ал
-
ұмтылғандағы
шексіз аз шама) түрінде көрсетуге болса
,
онда
шамасы
функциясының
нүктесіндегі
... деп аталады.
$$ дифференциалы
253.
Шекті
табыңыз:
.
$$
254.Функцияның
–
ретті
туындысы деп , оның
-ретті
туындысынан .... алуды айтады , егер бұл
туындылар бар деген шарт орындалса..
$$ туынды
255.Берілген
функцияның
иілу
нүктесін табыңыз:
$$
256.
Шекті
табыңыз:
$$0
257.
Табу
керек
,
егер
$$
258.
Синус
функциясының
Маклорен
формуласы бойынша жіктелуін көрсетіңіз:
$$
259.
функциясы
(a,b)
аралығында
дифференциалданатын
болсын.
Егер
… ,
,
онда
функциясы
(a,b)аралығында
монотонды
кемиді.
$$
260.
Егер
нүктесінде
функциясы
үзіліссіз , ал осы нүктедегі функцияның
туындысы нольге тең немесе туындысы
жоқ болса, онда бұл нүктені функцияның
… нүктесі
деп атайды.
$$ кризис
261.Егер
және
функциялары
ұмтылғандағы шексіз аз немесе шексіз
үлкен функциялар
және
а
нүктесінің
маңайында
дифференциалданатын
болып ,
және
,
онда
егер
табылса,
онда
де
табылып:
$$
=
262. Косинус функциясының Маклорен формуласы бойынша жіктелуін көрсетіңіз:
$$
263.
Табу
керек
,
егер
.
264.Интегралды
есептеңіз:
.
$$
265.
Интегралды
есептеңіз
:
.
$$
266.
нүктесі
функциясының
...нүктесі деп аталады ,
егер
ол осы нүктенің қандай да бір
маңайында
анықталған және
.
$$ минимум
267.
интегралының
геометриялық
мағынасы:…
$$ қисық сызықты трапецияның ауданын есептеу
268. функциясы нүктесінде ... функция деп аталады , егер оның осы нүктеде ақырлы шегі бар болса.
$$ дифференциалданатын
269.
Интегралды
есептеңіз :
.
$$
270. Гиперболалық тангенс:
$$
271.
функциясы
аралығында
дифференциалданатын функция деп аталады
, егер
ол осы аралықта
… және
интервалының
барлық нүктелерінде туындысы бар болса.
$$ үзіліссіз
272.
нүктесі
функциясының
...нүктесі деп аталады ,
егер
ол осы нүктенің қандай да бір
маңайында
анықталған және
.
$$ максимум
273.
Интегралды
есептеңіз :
.
$$
274.
қисығының
эксцентриситеті:
$$
275.
функцияның
туындысын табыңыз:
$$
276. функциясы (a,b) аралығында дифференциалданатын болсын . Егер функциясы (a,b) аралығында монотонды өсетін болса , онда үшін.… .
$$
277. функциясы кризистік нүктесінің қандай да бір маңайында дифференциалданатын функция және бар болсын. Онда, егер … болса , - максимум нүктесі болады.
$$
278.
қисығының
эксцентриситеті:
$$
279. функциясы кризистік нүктесінің қандай да бір маңайында дифференциалданатын функция және бар болсын. Онда, егер … болса , - минимум нүктесі болады.
$$
280.
гиперболасының
фокустары ... нүтесінде орналасқан.
$$
281.
шеңберінің
радиусын анықтаңыз.
$$ 6
282.
шеңберінің
центрі
мен радиусын
табыңыз.
$$
283.
параболасының
фокустары.... нүктесінде орналасқан.
$$
284.
эллипсінің
фокустары ... нүктелерінде орналасқан.
$$
285.
функциясының
туындысын табыңыз.
$$
286. Нақты жарты осі Ох бар эллипстің канондық теңдеуі:
$$
287.
шеңберінің
центрін анықтаңыз.
$$
288. Екінші тамаша шек:
$$
289.
гиперболасының
жарты осін анықтаңыз:
$$
290.
теңдеуімен
берілген сфераның центрі
мен
радиусын
табыңыз.
$$
291.
Эллипстің
теңдеуін жазыңыз ,
егер
.
$$
292. Бірінші тамаша шек формуласы:
$$
293.
Шекті
есептеңіз:
$$ 1
294. Егер А жиынының әрбір элементі В жиынының да элементі болса, онда А жиыны В жиынының ... деп аталады.
$$ ішкі жиыны
295.
функциясының
нүктесіндегі
мәнін табыңыз:
$$ 1
296.
функциясының
туындысын табыңыз:
$$
297.
функциясының туындысын табыңыз:
$$
298.
функциясының туындысын табыңыз:
$$
299.
функциясының туындысын табыңыз:
$$
300.
функциясының туындысын табыңыз:
$$
301. функциясының дифференциалының формуласын көрсетініз:
$$
302.
туындының
. геометриялық
мағынасы :
$$ функцияның графигіне нүктесінде жүргізілген жанаманың бұрыштық коэффициенті
303.
Интегралды
табыңыз :
.
$$
304. функциясының анықталмаған интегралы деп …айтады.
$$ берілген үзіліссіз функцияның барлық алғашқы бейнелерінің жиынтығын
305.Анықталмаған интегралды табу процесін функцияны …деп атайды.
$$ интегралдау
306.
Интегралды
табыңыз :
$$ -16
307.
мен
сызықтарымен
шектелген фигура ауданын есептеңіз.
$$ 4/3
308.
Интегралды
табыңыз:
$$ 0
309. ОХ осіне параллель түзу теңдеуін жазыңыз
$$
310. ОУосіне параллель түзу теңдеуін жазыңыз.
$$
311. Координаттар басы арқылы өтетін түзу теңдеуін жазыңыз.
$$
312. нүктесі арқылы өтетін және бұрыштық коэффициенті бар түзу теңдеуін жазыңыз:
$$
313.
нүктелері
арқылы түзу теңдеуін жазыңыз:
$$
314.Координаттар басы арқылы өтетін жазықтық теңдеуін жазыңыз.
$$
315. Ох осіне параллель жазықтық теңдеуін анықтаңыз
$$
316 Оу осіне параллель жазықтық теңдеуін анықтаңыз.
$$
317. Жазықтықтың кесінділердегі теңдеуін анықтаңыз.
$$
318. Бір түзудің бойында жатпайтын әртүрлі үш нүкте арқылы жазықтық теңдеуі:
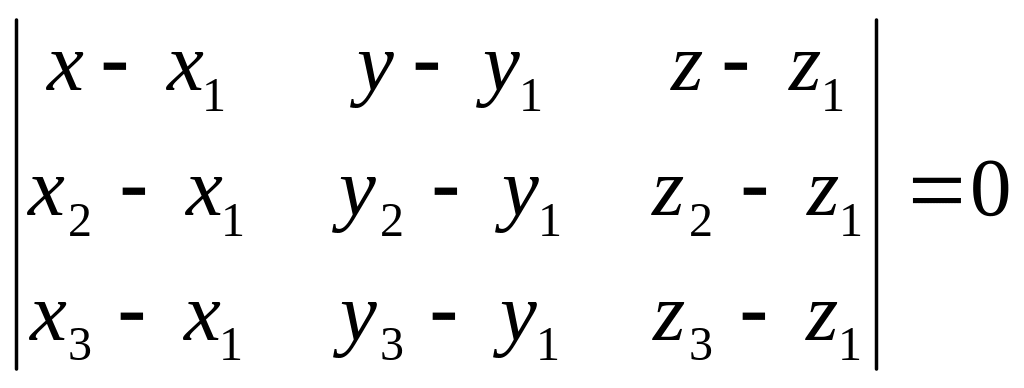
$$
319.
функциясының туындысын табыңыз.
$$
320.
функциясының
туындысын табыңыз.
$$
321. формуласы ...формуласы деп аталады.
$$ Ньютон-Лейбниц
322. Шектері шексіздіктер болатын интегралдар қалай аталады :
$$ меншіксіз интегралдар
323. Oz осіне параллель болатын жазықтық теңдеуін анықтаңыз
$$
324. OXY.координаталық жазықтығына параллель болатын жазықтық теңдеуін анықтаңыз.
$$
325. Жазықтықтың нормаль теңдеуін анықтаңыз:
$$
326.
Жазықтықтағы
мен
нүктелерінің
арақашықтығы келесі формуламен
анықталады:
$$
327. Түзудің ОХУ жазықтығындағы жалпы теңдеуін анықтаңыз:
$$
$
$
$
328.
түріндегі
түзулер
…деп
аталады.
$$ директрисалар
329. Түзудің кесінділердегі теңдеуі:
$$
330. Анықталу облысы болатын функциясы тақ функция деп аталады , егер келесі шарт орындалса:
$$
331.
тізбегі
шексіз үлкен деп аталады егер
…
$$
332.Интегралды
есептеңіз:
:
$$
333. OXZ координаттық жазықтығының теңдеуін анықтаңыз
$$
334. OYZ.координаттық жазықтығының теңдеуін анықтаңыз.
$$
335.
функциясының туындысын табыңыз:
$$
336.
функциясының туындысын табыңыз:
$$
337
Сызықтың
теңдеуі
полярлық
координаталарымен
:
берілген .
Оны
декарттық
координаталарда
жазыңыз.
$$
338.
мен
-ның
қандай мәндерінде
мен
векторлары
коллинеар
болады?
$$
339.
Басы
О(0;0) нүктесінде
жататын , ал ұшы В(4;
8) нүктесінде
жататын
жарты
кубтық параболаның доғасының ұзындығын
табыңыз.
$$ 64/5
340.
параболасының
параметрін табыңыз.
$$ 3
341. Центр деп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын …деп атайды.
$$ шеңбер
342. Гиперболаның асимптоталарының теңдеуінің түрі:
$$
343.Жиынды құрайтын объектілерді ол жиынның …деп атайды.
$$ элементтері
344. Еш элементі жоқ жиын …жиын деп аталады.
$$бос
345. А мен В жиындарының екеуінде де жататын ортақ элементтерінен құралған және басқа элементтері жоқ жиынды осы А және В жиындарының …деп атайды.
$$ қиылысуы (көбейтіндісі)
346.Элементтері сандар болатын жиын ... жиын деп аталады.
$$ сандық
347. Әрқайсысы үшін х- аргументтің мәні болатын ,ал у –оған сәйкес функцияның мәні болатын Оху жазықтығының барлық нүктелерінің жиынын функциясының .... деп атайды.
$$ графигі
348. Кесінділер , интервалдар және жартыинтервалдар ... аралықтар деп аталады.
$$ сандық
349.
нүктесі
тиісті
интервалы
нүктесінің
.... деп аталады.
$$ маңайы
350.
а
саны
тізбегінің
... деп аталады,
егер
кез келген
саны
үшін
саны
табылып
орындалатын барлық
сандары
теңсіздігін
қанағаттандырса.
$$ шегі
351.
А
саны
функциясының
ұмтылғандағы
... шегі деп
аталады,
егер
.
$$ сол жақ
352.
А
саны
функциясының
ұмтылғандағы
... шегі деп
аталады,
егер
.
$$ оң жақ
353.
және
нүктелері
мен
нүктесі
кесіндісін
қатынаста
бөлетін болса , онда ол нүктенің
координаталары келесі формулалармен
анықталады:
$$
354. Эллипстің директрисалары деп келесі түрдегі түзулерді айтады:
$$
355.
Центрі
нүктесінде
, радиусы
3
тең шеңбердің теңдеуін жазыңыз.
$$
;
356. теңдеуімен берілген қисықтың түрін анықтаңыз.
$$ эллипс
357.
және
нүктелері берілген.
-ның
қандай мәнінде
АВ векторының
ұзындығы
тең
?
$$ 6
358.
Шекті
табыңыз:
$$ 4
359.
Шекті
табыңыз:
$$
360.
функциясының туындысын табыңыз:
$$
