1.Види матриць.

Нульова матриця.

Матриця протилежна матриці А.

Трапецієвидна (ступінчаста) матриця.

Матриця-рядок.

Матриця-стовпець.

Верхня трикутна матриця.

Нижня трикутна матриця.

Діагональна матриця.

Скалярна матриця.

Одинична матриця.

Дії з матрицями:

Додавання матриць. С=А+В.

Віднімання матриць. А-В=А+(-В).

Множення матриць на число. С=αА

Множення матриць. С=А*В.

Транспонування матриць.( стовпчики міняються з рядками).

2.Визначники.

Визначником n-го порядку квадратної числової матриці А порядку n називають число, яке знаходиться з елементів матриці А за певним правилом і позначають ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌|А| або (А).

Правило знаходження визначника 2 порядку: визначник 2 порядку дор. різниці добутків елементів головної та допоміжної діагоналей, тобто: а₁₁*а₂₂ – а₁₂*а₂₁

Правило знаходження визначника 3 порядку: а₁₁*а₂₂*а₃₃+а₁₂*а₂₃*а₃₁+а₂₁-а₃₂*а₁₃-а₁₃*а₂₂*а₃₁-а₁₂*а₂₁*а₃₃-а₃₂*а₂₃*а_11. (правило Саріуса).

Властивості визначників:

Визначник при транспонуванні не змінюється (праві часнини рівні, тому і ліві частини рівні, тобто . Наслідок: У визначник рядки та стовпці мають однакові властивості.

Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінить знак на протилежний.

Якщо визначник має два однакових рядки (стовпця), то він дорівнює нулю.

Якщо у визначнику усі елементи одного рядка (стовпця) помножити на однакове дійсне число k, то визначник зросте також в k разів. Наслідок 1. Спільний множник усіх елементів будь-якого рядка (стовпця) визначника можна винести за знак визначника. Наслідок 2. Якщо усі елементи будь-якого рядка (стовпця) визначника дорівнюють нулю, то визначник дорівнює нулю.

Визначник, у якого відповідні елементи двох будь-яких рядків (стовпців) пропорційні, дорівнює нулю.

Якщо у визначнику елементи і-го рядка (k-го стовпця) є сумою двох доданків, тоді він дорівнює сумі двох відповідних визначників.

Якщо до всіх елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця) цього визначника, помножені на одне й те ж саме число, то визначник не зміниться.

3. Мінори та алгебраїчні доповнення.

Означення 1. Мінором М_ij елемента а_ij визначника n-го порядку називається визначник (n-1) порядку, який одержуємо з визначника |A| шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент а_ij. Мінор, який не дорівнює нулю, та має порядок, рівний рангу , називають базисним мінором.

Означення 2. Алгебраїчним доповненням А_ij елемента а_ij визначника називають мінор цього елемента, взятий зі знаком (-1)^i+j , тобто ^i+jM_{i j}.

4. Розкладання визначника за елементами рядка або стовпця.

По елементам і-го рядка: 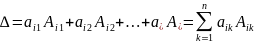По елементам j-го стовпчика:

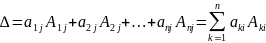
5.Практичні способи обчислення визначників.

Правило обчислення визначника n-го порядку: Визначник n-го порядку дорівнює сумі добутків уcіx елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення.

Отже, обчислення визначника порядку зводиться до обчислення визначників (n-1) порядку шляхом розкладу визначника за елементами будь-якого рядка або стовпця.

6.Поняття невиродженої матриці.

Невироджена матриця (неособлива, несингулярна, інвертована) — квадратна матриця, визначник якої не дорівнює нулю: det A 0.

Властивості:

Рядки і стовпці виродженої матриці лінійно незалежні.

Ранг матриці дорівнює розмірності матриці.

У не виродженої матриці є обернена матриця. Це еквівалентно тому, що лінійний оператор, який задається матрицею А є бієкцією векторного простору.

Якщо матриця A— не вироджена, то система рівнянь Ax=0 має тільки нульовий розв'язок.

Матриця є не виродженою тоді і тільки тоді якщо всі її власні значення є ненульовими.

Обернена матриця.

Означення: Матриця А^-1 на зивається оберненою матрицею до матриці А, якщо виконуються рівності:

Тобто матриці А та А^-1 комутують і їх добуток є одинична матриця.

Умови оберненої матриці:

матриця А квадратна.

визначник |А| матриці А не дорівнює нулю.

Обернену матрицю А^-1 до матриці А можна знаходити 2 способами:

за формулою: .

З використанням означення оберненої матриці та елементарних перетворень матриць.

7.Ранг матриці.

Означення: Рангом матриці називають найбільший порядок її мінорів, відмінних від нуля.

Елементарні перетворення матриці.

Елементарними перетвореннями матриці називають слідуючі перетворення:

перестановка рядків (стовпців) матриці;

множення всіх елементів рядка (стовпця) на число λ 0;

додавання до елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на деяке число.

8.Поняття системи лінійних рівнянь

Означення 1: Система алгебраїчних рівнянь називається лінійною, якщо вона може бути записана у вигляді:

a₁₁ x₁ +a₁₂ x₂+…+a_1k x+…+a_1n x_n=b

a₂₁ x₁ +a₂₂ x₂+…+a_2k x+…+a_2n x_n=b

a_i1 x₁ +a_ik x₂+…+a_ik x+…+a_in x_n=b

… … … …

a_m1 x₁ +a_m2 x₂+…+a_mk x+…+a_mn x_n=b

Якщо b_k= 0 для усіх k= 1,2,…, m, тоді систему називають однорідною. Якщо хоч би один вільний член b_k не дорівнює нулю, тоді система алгебраїчних рівнянь називається неоднорідною.

Означення: Система лінійних алгебраїчних рівнянь, що має хоч би один розв’язок, називається сумісною, а система, що не має розв’язку, називається несумісною.

9.Розв’язування систем n лінійних рівнянь з n невідомими.

Для розв’язування неоднорідної системи 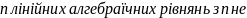відомимиматричним методом доцільно здійснювати такий порядок дій:

записати основну матрицю системи А і знайти її визначник (А). Яещо (А)= 0, то система розв’язку не має.

якщо (А) 0, тоді знайти обернену матрицю 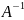до матриці А.

помножити обернену матрицю на матрицю-стовпець вільних членів системи.

Формула Крамера.

Прваило Крамера. Якщо основний визначник (А) неоднорідної системи n лінійних алгебраїчних рівнянь з n невідомими не дорівнює нулю, то ця система має єдиний розв’язок, який знаходиться за формулами:

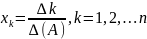
Де 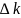– допоміжний визначник, який одержується з основного визначника шляхом заміни його -го стовпця стовпцем вільних членів системи.

10.Розв'язування систем п лінійних рівнянь з п невідомими за допомогою оберненої матриці.

11. Розв'язування систем т лінійних рівнянь з п невідомими. Метод Гаусса.

якщо основний визначник неоднорідної системи n лінійних алгебраїчних рівнянь з n невідомими не дорівнює нулю, то ця система має єдиний розв'язок.

Алгоритм кроку перетворення Гаусса-Жордана:

обираэмо розв'язувальний елемент

елементи і-го рядка (його називають розв’язувальним) ділимо на і запишемо в рядок розрахункової таблиці;

в розв’язувальному стовпці замість пишуть одиницю, а замість інших елементів цього стовпця пишуть нулі;

усі інші елементи розрахункової таблиці, в тому числі і контрольного стовпця, знаходять за формулою: Обчислення елементів схеми прямокутника.

Роблять перевірку правильності розрахунків шляхом порівняння суми елементів рядка з відповідним елементом контрольного стовпця.

12.Теорема Кронекера-Капеллі про сумісність системи лінійних рівнянь.

Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг її матриці А дорівнює рангу розширеної матриці 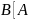| . Причому система має єдине рішення, якщо ранг дорівнює числу невідомих і нескінченно багато рішень, якщо ранг менше числа невідомих.

13.Модель міжнародної торгівлі.

Розглянемо лінійну модель міжнародної торгівлі, яка приводить

до поняття власного вектора і власного значення матриці.

Нехай є n країн S₁, S₂,..., S_n із національними доходами x₁, x₂,..., x_n

відповідно. Частку національного доходу, що країна Sj витрачає на за-

купівлю товарів у країни S_i, позначимо a_ij. Введемо структурну мат-

рицю торгівлі A і вектор національних доходів країн X:

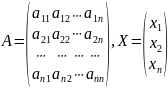
Вважаємо, що весь національний дохід витрачається на закупів-

лю товарів або всередині країни, або на імпорт з інших країн, тоді су-

ма елементів будь-якого стовпця матриці А дорівнює 1:

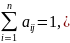
Виторг від внутрішньої і зовнішньої торгівлі країни S_i складе:

Для збалансованої торгівлі необхідна бездефіцитність торгівлі

кожної країни S_i, тобто виторг від торгівлі кожної країни повинний

бути не менше її національного доходу:

p_i ≥ x_i (i = l, 2,..., n).

При pi > xi (i = 1, 2, ..., п) одержуємо систему нерівностей

Склавши всі нерівності системи (2.20), одержимо:

х₁(а₁₁+а₂₁+...+а_n1)+х₂(а₁₂+а₂₂+...+а_n2)+…+(а_1n+а_2n+...+а_nn)x_n > х₁ + х₂ +…+х_n.

З огляду на (2.19), вирази в дужках дорівнюють одиниці, і ми

приходимо до суперечливої нерівності х1 + х2 +…+хn > х1 + х2 +…+хn.

Таким чином, нерівність pi > xi (i = l, 2,..., n) неможлива, і умова pi ≥ xi

набуде вигляду pi = xi (i = l, 2,..., n). З економічної точки зору це озна-

чає, що всі країни не можуть одночасно отримувати прибуток.

У матричному вигляді одержимо рівняння

AX = X, (2.21)

тобто задача звелася до знаходження власного вектора матриці А,

що відповідає власному значенню λ = 1.

14. Вектори на площині і у просторі. Дії над векторами. Координати вектора.

Вектором називають величину, якак характеризується не тільки своїм числовим значенням (довжиною), але й напрямком. Вектори позначають

Нульовим вектором називають вектор, початок і кінець якого співпадають. Такий вектор позначають а його довжина дорівнює 0, а напрям – довільний.

Рівними називають вектори, які мають однакові довжини та напрямки: .

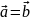Колінеарними називають вектори, які розташовані на одній прямій або паралельних прямих.

Протилежними наз. колінеарні протилежно спрямовані вектори однакової довжини.

Ортом вектора наз. вектор, довжина якого =1,а напрям співпадає з , тобто .

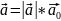Компланакними векторами називають вектори, що лежать в одній площині.

Проекцією вектора 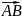на вісь називається довжина вектора 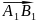, яка взята зі знаком «+», якщо напрям співпадає з напрямом осі та із знаком «-», якщо напрями протилежні.

Координатами вектора називаються проекції вектора на осі координат.

Координати вектора дорівнюють різниці відповідних координат кінця та початку вектора.

Дії з векторами.

Сумою двох векторів та 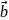зазивають вектор , який сполучає початок вектора з кінцем вектора при умові, що початок вектора вміщено в кінець вектора .

Добутком вектора 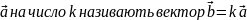, колінеарний з вектором , що має довжину в k раз більшу, ніж 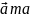напрям такий самий, як , якщо k>0 і протилежний до , якщо k < 0.

Скалярним добутком векторів 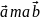називають число, яке дорівнює добутку модулів цих векторів на косинус кута між цими векторами.

Розклад вектора за базисом.

Лінійно залежними називають вектори , якщо існує хоч би одне дійсне число що не дорівнює нулю і виконується рівність:

.

Лінійно незалежними називають вектори , якщо рівність виконується тільки тоді, коли усі .

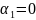Координати вектора.

Координати вектора називаються проекції вектора на осі координат.

Координати вектора дорівнюють різниці відповідних координат кінця та початку вектора.

15.Модуль вектора. Дії над векторами, заданими своїми координатами.

Довжина напрямленого відрізку визначає числове значення вектора і називається довжиною вектора або модулем вектора. Для позначення модуля вектора використовують дві вертикальні лінії зліва та справа .

Модуль вектора (довжина вектора) 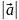в прямокутних декартових координатах дорівнює квадратному кореню з суми квадратів його координат.

Дії з векторами.

Сумою двох векторів та зазивають вектор , який сполучає початок вектора з кінцем вектора при умові, що початок вектора вміщено в кінець вектора .

Добутком вектора , колінеарний з вектором , що має довжину в k раз більшу, ніж напрям такий самий, як , якщо k>0 і протилежний до , якщо k < 0.

Скалярним добутком векторів називають число, яке дорівнює добутку модулів цих векторів на косинус кута між цими векторами.

Розклад вектора за базисом.

Лінійно залежними називають вектори , якщо існує хоч би одне дійсне число що не дорівнює нулю і виконується рівність:

.

Лінійно незалежними називають вектори , якщо рівність виконується тільки тоді, коли усі .

Дії над векторами, заданими своїми координатами.

При додаванні двох, або більше векторів їх відповідні координати додаються.

При відніманні векторів відповідні координати віднімаються.

При множенні вектора на число всі координати множаться на це число.

Скалярний добуток двох векторів дорівнює сумі добутків відповідних координат.

16. Умови колінеарності і компланарності векторів.

Колінеарними називають вектори, які розташовані на одній прямій або паралельних прямих.

Компланакними векторами називають вектори, що лежать в одній площині.

17. Координати точки поділу. Скалярний добуток векторів та його властивості.

Скалярним добутком векторів називають число, яке дорівнює добутку модулів цих векторів на косинус кута між цими векторами.

18. Різні види рівняння прямої.

Загальне повне рівняння будь-якої прямої декартових координатах , y має вигляд

Якщо хоч один коефіцієнт у рівнянні прямої дорівнює нулю, рівняння наз. НЕПОВНИМ.

Розташування прямої відносно осей координат залежить від коефіцієнтів

Рівняння прямої з кутовим коефіцієнтом

Рівняння прямої у відрізках

Канонічне рівняння прямої має вигляд

Тангенціальне рівняння прямої ξ x + η y = 1.

19. Нормальне рівняння прямої. Відстань від точки до прямої.

де p - Довжина перпендикуляра, опущеного на пряму з початку координат, а θ - Кут (виміряний в позитивному напрямі) між позитивним напрямом осі O x і напрямом цього перпендикуляра. Якщо p = 0 , То пряма проходить через початок координат, а кут задає кут нахилу прямої.

Відстань від точки до прямої

Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.

.

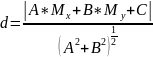20.Лінійні функції попиту і пропозиції, встановлення рівноважної ціни.

QD= С – d*Р (лінійна функція попиту). Ця функція – математичне вираження закону попиту, в якій виражено, як обсяг попиту на товар (Q) залежить від його ціни (Р).

Q_SA = f(P_A,P_B,…,P_Z,R,K,C,X…) – функція пропозиції.

Q_SA – обсяг пропозиції товару А в одиницю часу;

Р_A, P_B ..., Р_Z – ціни даного і решти товарів;

R – наявність виробничих ресурсів;

К – характер використання технологій;

С – податки і дотації;

Х – природно-кліматичні умови.

встановлення рівноважної ціни

Такий стан ринку можливий коли його кон'юнктура характеризується на графіці точкою Е (рівновага), що лежить на перетині кривих попиту і пропозиції. Тоді при даній кількості товару Q^* максимальна ціна, за якої можуть собі дозволити придбати його покупці (ціна попиту P^D), збіжиться з ціною, мінімально прийнятною для продавців (ціна пропозиції P^S), що і означатиме встановлення на даному ринку єдиної стійкої рівноважної ціни P^*, за якої і продаватиметься й купуватиметься рівноважна кількість товару Q^*.

У аналітичному вигляді, використовуючи зворотні функції попиту і пропозиції, це можна записати так: .

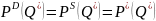21. Найважливіші криві другого порядку, їх канонічні рівняння.

Лінії другого порядку — геометричне місце точок на площині, декартові координати яких задаються рівнянням другого степеня: a₁₁x²+2a₁₂y²+a₂₂y² + 2a₁₃x+2a₂₃y+a₃₃=0, де хоча б один з коефіцієнтів a_11, a_12, a₂₂ відмінний від нуля.

еліпс

гіпербола

парабола

22. Множини. Дійсні числа. Числові проміжки, окіл точки.

Множина вважається означеною, якщо про кожен об'єкт, що розглядається, можна казати, що він або належить, або не належить множині. Ідентичні (тобто однакові) об'єкти в множині не допускаються.

На письмі множини позначаються, як правило, великими літерами. Для деяких множин у математиці вживаються сталі позначення. Наприклад:

ℕ - множина натуральних чисел,

ℤ - множина цілих чисел,

ℚ - множина раціональних чисел,

ℝ - множина дійсних чисел,

ℂ - множина комплексних чисел.

Дійсні числа — елементи певної числової системи, яка містить у собі раціональні числа і, в свою чергу, є підмножиною комплексних чисел.

Числовий проміжок-множина всіх дійсних чисел x, що задовольняють нерівності виду: a<x_a – позначення (a, +∞), або це аналогічно неточній нерівності, позначення [a, b], (-∞, a], [a, +∞); у першому випадку мають місце відкриті ч.п., а в другому - замкнені ч.п. (відкритість позначається круглою дужкою, замкненість - квадратною) <x.

Околом точки є множина, яка містить відкриту множину, що містить цю точку.