§ 7. Взаимное расположение двух прямых в пространстве.
Пусть прямые
и
заданы относительно некоторой аффинной
системы координат
каноническими уравнениями
, 
. 
Относительно друг друга прямые и могут занимать одно из четырех различных положений:
1. и скрещиваются,
.
Выявим условия, соответствующие каждой из указанных ситуаций.
1.
Если прямые
и
скрещиваются, то векторы
и
не компланарны. Это равносильно условию
,
которое в координатах принимает вид
(7.1)
2
.
Если
,
то векторы
и
– не коллинеарны, но векторы
– компланарны. Следовательно, выполняются
условия
Рис. 7.2.
и
. (7.2)
Рис. 7.3.
,
то
– компланарны,
– коллинеарны, а вектор
– не коллинеарен векторам
.
Это равносильно выполнению условий
,
которые в координатах принимают вид:
,
. (7.3)
4. Если
,
то векторы
– коллинеарны. Это равносильно условиям
и
,
которые в координатах принимают вид:
,
.
(7.4)
§ 8. Взаимное расположение прямой и плоскости.
Пусть относительно аффинной системы координат
заданы прямая и плоскость уравнениями
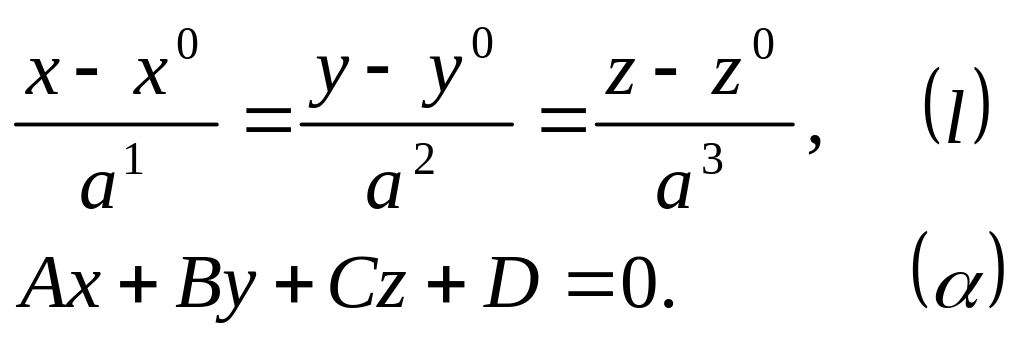(8.1)
Как известнее, прямая и плоскость в пространстве могут занимать относительно друг друга одно из трех различных положений:
1°.
,
2°.
,
3°.
.
Если имеет место первый случай, то прямая и плоскость имеют только одну общую точку, во втором случае общих точек нет, а в третьем – их бесконечное множество. Поэтому вопрос о взаимном расположении прямой и плоскости сведем к вопросу о количестве общих точек или о количестве решений системы уравнений (8.1).
Для этого запишем
уравнения прямой
в
виде
,
,
и подставим их в уравнение плоскости . В таком случае будем иметь равенство
или
. (*)
1. Если
(т.е.
не компланарен плоскости
),
то (*)
:
Это означает, что
и
пересекаются и имеют единственную общую
точку
.
2. Если
,
то (*)
,
Поэтому
3. Если
то
(*)
В этом случае любая точка прямой лежит на плоскости , т.е. .
§ 9. Угол между прямой и плоскостью.
Пусть в прямоугольной
декартовой системе координат
заданы прямая
и плоскость
соответственно уравнениями
, .
П
од
углом между прямой
и плоскостью
понимают
угол
между прямой
и ее ортогональной проекцией
на плоскость
:
.
Пусть
– направляющий вектор прямой
и
– нормальный вектор плоскости
.
Обозначим через
.
Тогда
и
Поэтому
.
Таким образом, угол между прямой и плоскостью можно найти по формуле
. (9.1)
1. Если
,
то
и
– коллинеарны
. (9.2)
2. Если
,то
. (9.3)
§ 10. Угол между двумя плоскостями.
Пусть относительно заданы плоскости и общими уравнениями
,
.
и
– нормальные векторы этих плоскостей.
Угол между
плоскостями
и
определим как угол
Тогда
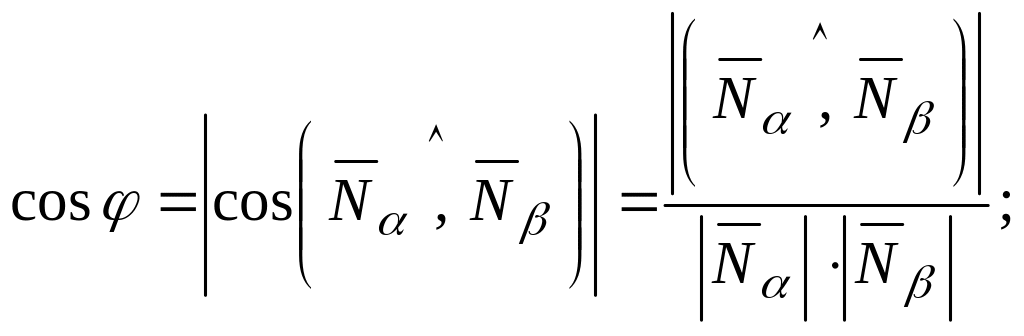
или 
. (10.1)
если
,
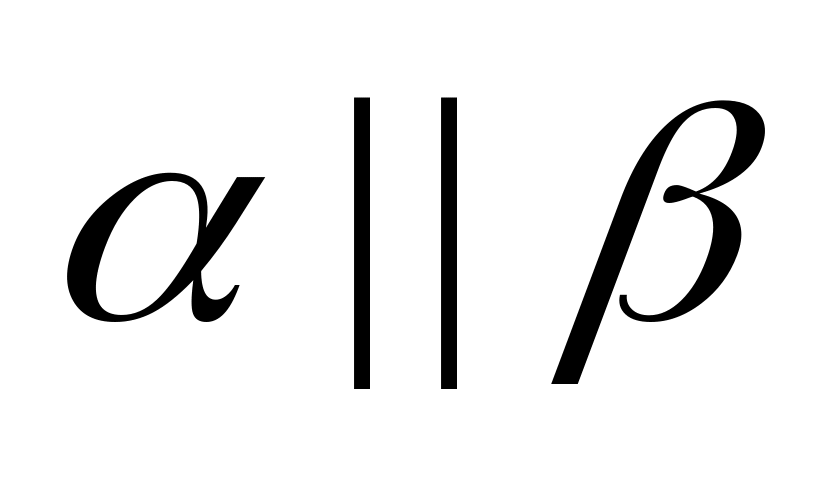то
и
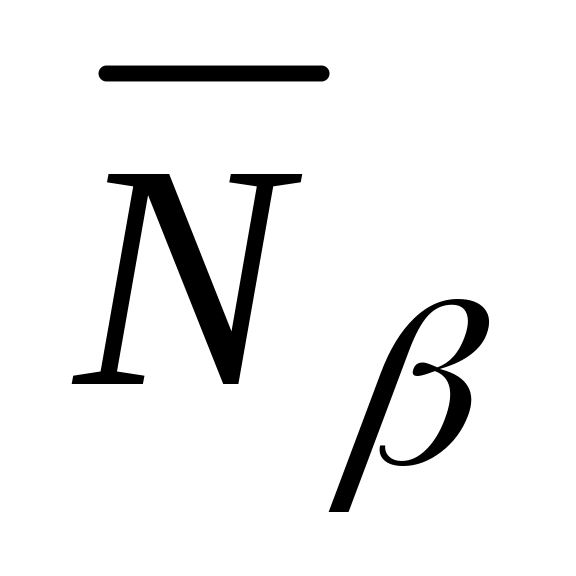коллинеарны
(10.2)
если
,
то и
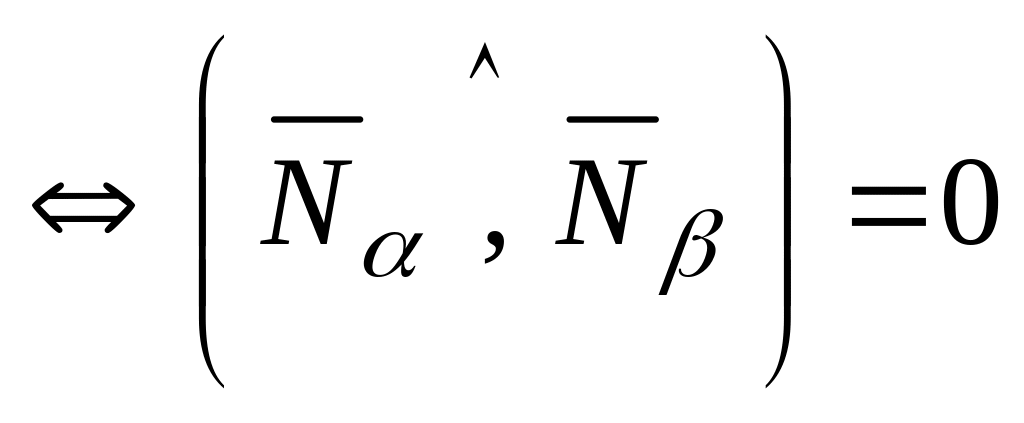
(10.3)