
- •Раздел 3. Плоскость и прямая в пространстве
- •§ 1. Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам.
- •§ 2. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках.
- •§ 3. Общее уравнение плоскости.
- •§ 4. Взаимное расположение двух плоскостей в пространстве.
- •§ 5. Уравнение прямой, проходящей через точку в данном направлении.
- •§ 6. Общие уравнения прямой в пространстве.
- •§ 7. Взаимное расположение двух прямых в пространстве.
- •§ 8. Взаимное расположение прямой и плоскости.
- •§ 9. Угол между прямой и плоскостью.
- •§ 10. Угол между двумя плоскостями.
- •§ 11. Нормальное уравнение плоскости.
- •§ 12. Расстояние от точки до плоскости.
Раздел 3. Плоскость и прямая в пространстве
§ 1. Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам.
Положение плоскости относительно некоторой аффинной системы координат можно определить (задать) различными способами. Каждому такому способу задания будет соответствовать вполне определенное ее уравнение.
Определение. Вектор называют параллельным (принадлежащим) плоскости, если он коллинеарен некоторому вектору, лежащему на прямой этой плоскости.
 Пусть в
некоторой аффинной системе координат
Пусть в
некоторой аффинной системе координат
![]() задана плоскость
задана плоскость
![]() :
:
![]()
![]() ,
где
,
где
![]() и
и
![]() ,
и
,
и
![]() – не коллинеарны.
– не коллинеарны.
![]()
Пусть точка
![]() .
Найдем уравнение плоскости
.
.
Найдем уравнение плоскости
.
Тогда
![]() векторы
векторы
![]() – компланарны.
– компланарны.
![]()
![]() ,
а так как
,
а так как
![]() ,
то
,
то
![]() или
или
![]() (1.1)
(1.1)
Соотношение (1.1) называют векторно-параметрическим уравнением плоскости. Покоординатная запись уравнения (1.1) имеет вид
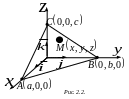
 (1.2)
(1.2)
Ее называют параметрическими уравнениями плоскости .
Условие
![]() равносильно соотношению
равносильно соотношению
![]() ,
которое в координатах принимает вид
,
которое в координатах принимает вид
 .
(1.3)
.
(1.3)
Равенство (1.3) называют уравнением плоскости, проходящей через точку параллельно двум неколлинеарным векторам.
Замечание.
Точку
![]() и два неколлинеарных вектора
и два неколлинеарных вектора
![]() и
и
![]() можно рассматривать как некоторую
«внутреннюю» аффинную систему координат
можно рассматривать как некоторую
«внутреннюю» аффинную систему координат
![]() в плоскости
.
В этом аффинном репере координатами
произвольной точки
в плоскости
.
В этом аффинном репере координатами
произвольной точки
![]() плоскости
будут значения
плоскости
будут значения
![]() ее
векторно-параметрического уравнения
(1.1).
ее
векторно-параметрического уравнения
(1.1).
§ 2. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках.
Пусть относительно
общей декартовой системе координат
задана плоскость
![]() ,
проходящей через три точки
,
проходящей через три точки
![]()
Так как
![]() и
и
![]() ,
то векторы
,
то векторы
![]()
![]() и
и
![]()
компланарны. Тогда
![]()
Последнее соотношение в координатах имеет вид:
 (2.1)
(2.1)
Равенство (2.1) называют уравнением плоскости, проходящей через три точки.
Пусть теперь
плоскость
проходит через три точки
![]() ,
,
![]()
![]() ,
ни одна из которых не совпадает с началом
координат.
,
ни одна из которых не совпадает с началом
координат.
Тогда из (2.1) получаем:
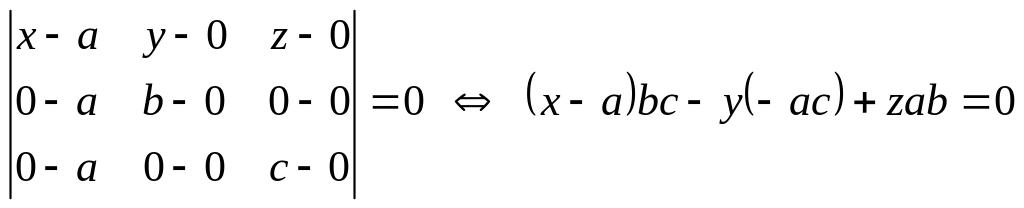
или
![]()
![]() (2.2)
(2.2)
Соотношение (2.2) называют уравнением плоскости в отрезках.
§ 3. Общее уравнение плоскости.
Из уравнения (1.3) следует
![]()
Пусть
![]() Тогда (*)
Тогда (*)
![]()
![]() или
или
![]() ,
(3.1)
,
(3.1)
где
![]()
А так как
![]() и
и
![]() не
коллинеарны, то
не
коллинеарны, то
![]() или
или
![]() или
или
![]() ,
т.е.
,
т.е.
![]() (3.2)
(3.2)
Таким образом,
плоскость определяется уравнением
первой степени относительно переменных
![]()
Справедливо и обратное утверждение.
Теорема 3.1.
Всякое уравнение первой степени (3.1)
относительно переменных
![]() при условии (3.2)
определяет в аффинной системе координат
некоторую плоскость.
при условии (3.2)
определяет в аффинной системе координат
некоторую плоскость.
▼ Пусть
![]() Тогда
уравнение (3.1)
Тогда
уравнение (3.1)
![]()
В ведем
в рассмотрение два параметра
и
ведем
в рассмотрение два параметра
и
![]() .
Тогда (*)
.
Тогда (*)

Получили параметрические уравнения плоскости. Следовательно, уравнение (3.1) при условии (3.2) действительно определяет плоскость.
Теорема 3.2.
Вектор ![]()
![]()
![]() (3.3)
(3.3)
▼ Необходимость.
Пусть
![]() ,
где
,
где
![]() ,
,
![]() .
Тогда
.
Тогда
![]() и
и
![]()
![]() .
.
Следовательно
![]() или
или
Достаточность. (Доказать самостоятельно).
Частные случаи общего уравнения плоскости:



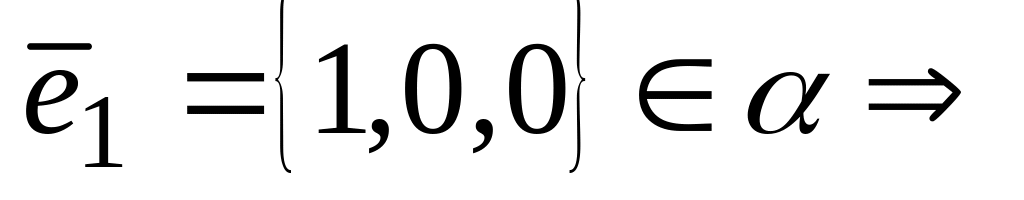

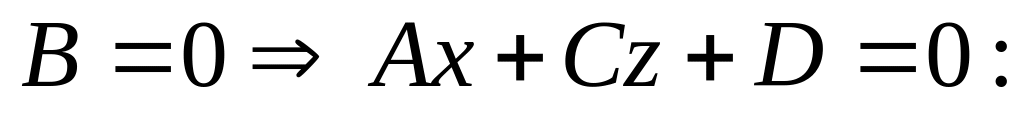



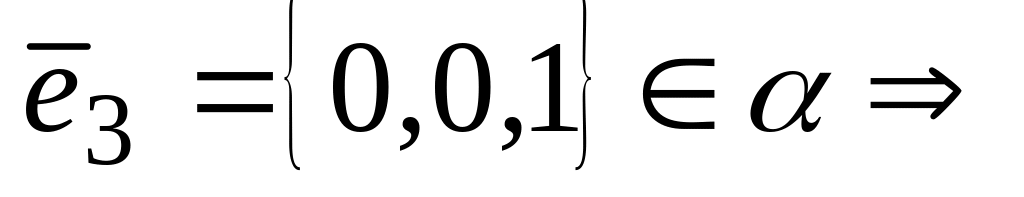
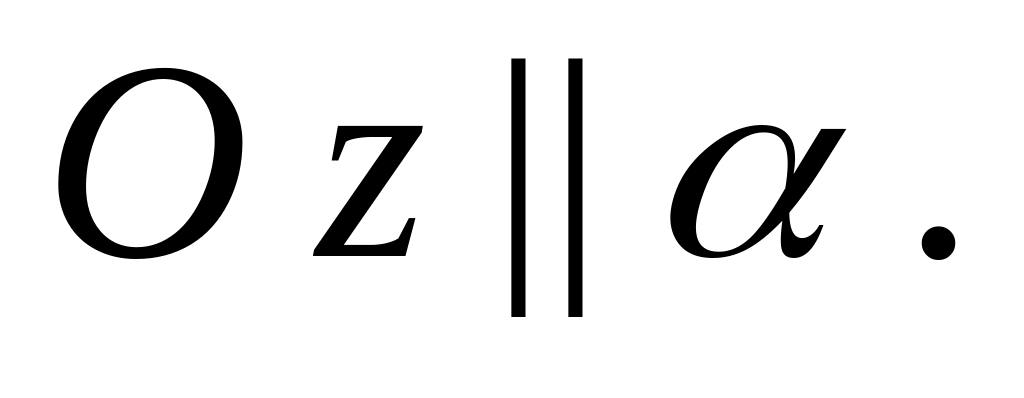
 1º и 2º
1º и 2º
 1º и 3º
1º и 3º
 1º и 4º
1º и 4º

 2º
и 3º
2º
и 3º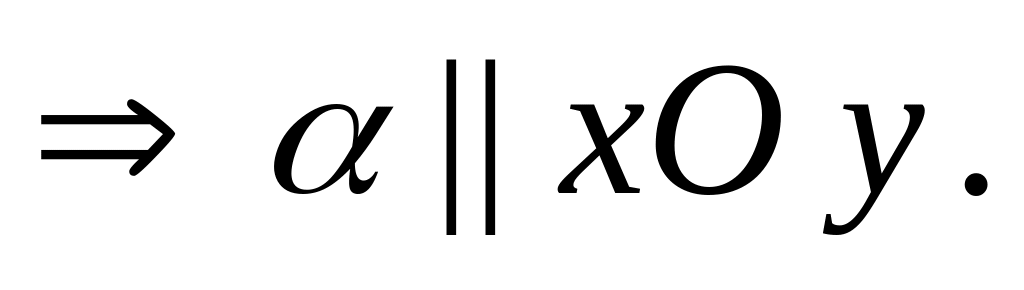

 3º
и 4º
3º
и 4º

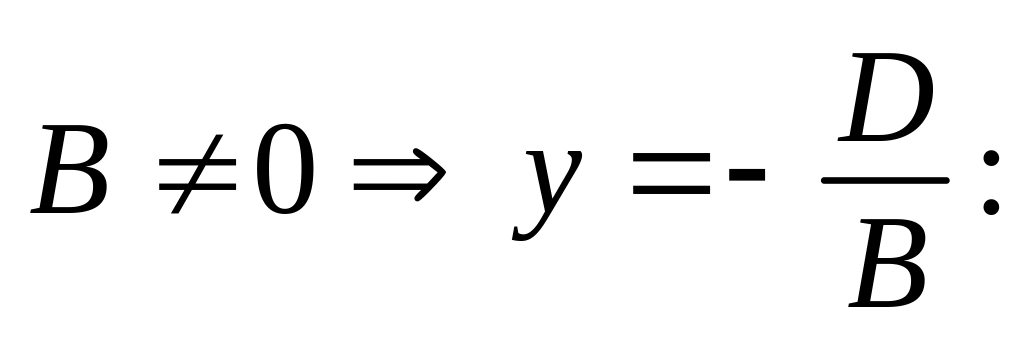 2º
и 4º
2º
и 4º


 1º,
2º, 3º
1º,
2º, 3º


 1º,
3º, 4º
1º,
3º, 4º
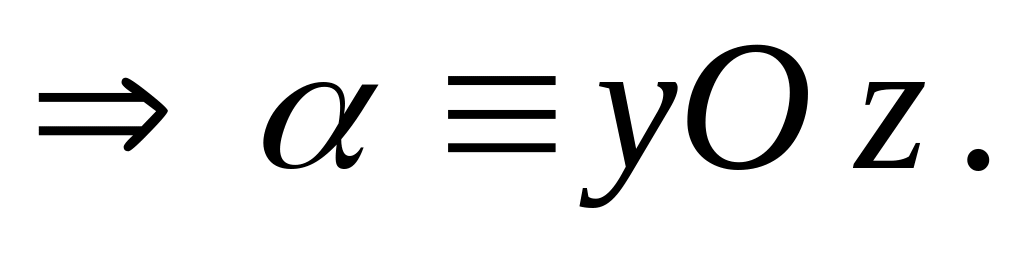

 1º,
2º, 4º
1º,
2º, 4º

Определение.
Вектор
![]() называют главным вектором плоскости
(3.1).
называют главным вектором плоскости
(3.1).
Вектор
![]() не коллинеарен плоскости
.
не коллинеарен плоскости
.
Действительно, используя теорему 3.2, получаем
![]()
Пусть дана
прямоугольная система координат
![]() ,
в которой плоскость
задана
общим уравнением (3.1).
,
в которой плоскость
задана
общим уравнением (3.1).
Если вектор
![]() коллинеарен плоскости
,
то
коллинеарен плоскости
,
то
![]()
Определение. Всякий ненулевой вектор, перпендикулярный вектору плоскости, называют нормальным вектором плоскости.
Таким образом, в прямоугольной декартовой системе координат главный вектор плоскости является ее нормальным вектором.
