
- •1.1. Поняття: дані, інформація, знання
- •1.2. Інформаційні системи та їх класифікація
- •1.3. Поняття про географічні інформаційні системи (гіс). Історія розвитку гіс
- •1.4. Відмінність гіс від інших систем. Завдання, які вирішують гіс.
- •1.4.1. Системи автоматизованого проектування (сапр)
- •1.4.2. Системи автоматизованого картографування (акс)
- •1.4.3. Системи управління мережами (ам/fм)
- •1.4.4. Система управління базами даних (субд)
- •1.4.5. Класифікація гіс
- •2.1. Організація інформації в гіс
- •2.1.1. Просторова інформація
- •2.1.2. Системи координат
- •2.1.3. Умовні знаки
- •2.1.4. Поняття масштабу
- •2.1.5. Номенклатура й розграфлення карт
- •2.1.6. Організація даних
- •2.2. Моделі даних
- •2.2.1. Векторна модель
- •2.2.2. Векторно-топологічна модель
- •2.2.3. Растрові моделі
- •2.2.4. Порівняння векторних і растрових моделей
- •3.1. Апаратні засоби
- •3.2. Програмні засоби гіс
- •3.2.1. Arc/info
- •3.2.2. ArcView gis
- •3.2.3. Er das Imaging
- •3.2.4. Er Mapper
- •3.2.5. Easy Trace
- •3.2.6. MapEdit для Windows
- •4.2.7. CaDdy
2.2.2. Векторно-топологічна модель
Векторна модель, яка описує не тільки геометрію об’єктів, але й топологічні відношення між ними, отримала назву векторно-топологічна модель. [18, 26, 64, 67]
Топологічні структури даних надають додаткового змісту накопиченій інформації. Вони вказують, які просторові об'єкти зв'язані один з одним логічно, тобто на багатокутник, що обмежений певними лініями, які мають певні початкові та кінцеві точки.
Таким чином, структури топологічних даних визначають як точки, лінії і багатокутники, що зв'язані один з одним на карті, тобто мають приховані взаємовідносини, які очевидні людському оку, але не ясно виражені для комп'ютера, коли він зчитує просторові дані в тому вигляді, як вони були подані до цього. Топологічні дані складаються з записів, що містять атрибути, які визначають, наприклад, що лінія відображає вуличний сегмент, який зв'язує дві точки перетину, і є також одною стороною кварталу (багатокутника). Топологічні дані визначають точку перетину вулиць як вузол (node) на вуличній мережі, що зв'язує два й більше вуличних сегментів (line segment, segment) у безперервний шлях.
У побудові топологічних моделей використовують графічне подання карт як плоских графів (graph).
Полігони, лінії і точки зображуються гранями й вузлами. Кожна грань обмежена початковим і кінцевим вузлом, до того ж відомо, які області знаходяться ліворуч і які праворуч. Теоретичні основи спираються на тoпологію і теорію графів. Сполучення теорії графів і топології дозволяє одночасно використовувати той і інший підходи. У більшості своїй сучасне математичне забезпечення ГІС базується саме на топологічних моделях.
Топологія - це математична дисципліна, яка займається визначенням просторових зв’язків, що зберігаються при безперервних деформаціях і перетвореннях.
Відносно карт, топологія визначає зв’язки між об’єктами, встановлює сусідство полігонів і подає один об’єкт (полігон) у вигляді набору інших об’єктів (ліній).
При розгляді топологічних взаємозв’язків абстрагуються від змістовних властивостей об’єктів і розглядають тільки топологічні характеристики об’єктів, їх метрику.
Об’єкти можуть бути точковими, лінійними і полігональними. Між цими елементами встановлюються зв’язки на рівні опису імен.
Топологія визначає всі об’єкти карти, як набір ліній (дуг), міток і як просторові відношення між точками і лініями, що з’єднуються (див. Рис.10.)[18].
Внутрішні точки (пари х,у) дуги, які називаються вершинами (vertex), задають форму дуги. Кінцеві точки дуги називаються вузлами. Кожна дуга має два вузли: початковий вузол і кінцевий вузол. Дуги можуть з’єднуватися тільки в кінцевих точках, визначаючи зв’язність дуг за наявністю загального вузла.

вершина
вузол
лінія
полігон
Рис.10.
Полігони подаються послідовностями координат х,у, які з’єднуються, утворюючи межу площинного об’єкта (контур, area) або як список дуг, що утворюють його межу, включаючи дуги, які визначають острови всередині полігона. Для полігональних об’єктів, включаючи об’єкти, зображені позамасштабними знаками, сукупність контурів визначає зайняту об’єктом багатозв’язну область від решти карти. При цьому розглядають зовнішній (?) і внутрішній (?) контури.
 Така
векторно-топологічна модель називається
також лінійно-вузловою
(arc-node model). Ця модель визначає основні
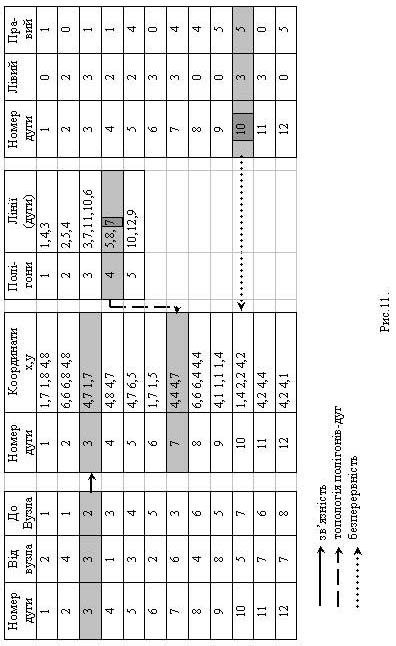
топологічні характеристики (Рис.11.)[18]:
Така
векторно-топологічна модель називається
також лінійно-вузловою
(arc-node model). Ця модель визначає основні
топологічні характеристики (Рис.11.)[18]:
-дуги з’єднуються між собою у вузлах (зв’язність);
-дуги, обмежуючи фігуру, визначають полігон;
-дуги мають напрямок, а також лівий і правий бік (безперервність).
Кожна дуга має напрямок (початковий і кінцевий вузли), тобто можливість визначити список полігонів ліворуч і праворуч від дуги. Таким чином полігони, які мають спільну дугу, є суміжними.
Побудова топології має на меті подання основних топологічних характеристик для всіх об’єктів лінійно-вузлової моделі за допомогою кількох простих атрибутивних таблиць (див. Рис.11.), які не містять у своїх атрибутах координатних характеристик. Ці таблиці називаються топологічними.
Можна навести приклади топологічних властивостей, які виконують не для всіх об’єктів лінійно-вузлової моделі. Наприклад, дуга може бути замкненою чи незамкненою; висячою чи ні; полігон може мати острови, а може й не мати; дві дуги можуть не мати спільних точок, а можуть мати спільні вузли; два полігони мають спільні дуги чи не мають; характер сусідства двох полігонів: тільки за вузлами, тільки за дугами, одночасно і за вузлами і за дугами, не перетинаються.
Ці відомості також можуть бути отримані із топологічних таблиць після побудови топології.
Топологічне вирішення завдання ідентифікації всіх контурів даного полігона достатньо прозоре й потребує розгляду топологічних зв’язків між дугами, що утворюють межу тільки цього полігона. А вирішення завдання визначення саме "великого” контуру серед усіх контурів даного полігона є складним топологічним завданням, розв’язання якого потребує залучення алгоритмів теорії графів та аналізу топологічних відношень між дугами не тільки конкретного полігону, але й між дугами інших полігонів лінійно-вузлової моделі.
Лінійно-вузлова модель подання просторових об’єктів разом з топологічними таблицями в сукупності дозволяють ефективно реалізувати специфічну просторово - аналітичну обробку даних, яка є ядром ГІС і становить набір функцій типу просторової вибірки, оверлейних операцій, вилучення дуг між сусідніми полігонами і таке інше.
Для аналізу топологічних зв’язків між об’єктами застосовуються такі відношення:
-суміжність (contiguity) - наприклад, для полігональних об’єктів - зображення двох суміжних будівель; для лінійних - зображення річки та межі, яка проходить по одному з берегів;
-сусідство (vicinity) - наприклад, для полігональних - два зображення будівель, які стоять поруч, для лінійних - зображення річки і розташованої поруч з річкою дороги;
-еквідистантне сусідство (equidistant vicinity) - наприклад, дві будівлі, розташовані паралельно одна одній чи паралельно розташовані залізниця і шосе;
-вкладеність (multiplicity) - наприклад, зображення острова вкладеного в зображення озера;
-накладення (superposition) - наприклад, для полігональних - зображення стінного репера, накладеного на зображення будівлі, для лінійних - зображення наземних і підземних комунікацій;
-перетин (intersection) - наприклад, зображення двох комунікацій, які перетинаються;
-примикання (contiguity) - наприклад, зображення двох прилеглих ділянок русла річки, що мають різні семантичні характеристики.
Більшість ГІС здатні оперувати з обома моделями векторних даних, і це дозволяє здійснювати операції експорту/імпорту графічної інформації.
