Статья II.Описание функционирования математической модели

1. Вычисление показателей эффективности смо

1. Расчет времени поступления заявок в СМО

^,

где λ – интенсивность потока заявок;

R - случайная величина, равномерно распределенная в интервале (0,1);

Т_k-1 – время поступления предыдущей заявки.

2.  Расчёт интервала времени между двумя последовательными заявками (между k-й и k+1)

^.

3. Расчёт момента поступления следующей заявки

_.

4. Расчёт времени обслуживания заявки по экспоненциальному закону распределения времени обслуживания:

.

5. Расчёт времени ожидания заявки на обслуживание:

,

где - время ожидания заявки в очереди;

- время освобождения канала, в который поступает заявка на обслуживание;

- время поступления заявки в СМО.

6. Расчёт среднего времени ожидания:

,

где N – количество поступивших заявок в СМО.

7. Расчёт среднеё длины очереди:

q = k – S ,

S = m∙U ,       

где q – среднее число заявок в очереди (средняя длина очереди);

S – среднее число заявок на обслуживании (в каналах), или среднее число занятых каналов;

k – среднее число заявок в СМО, т.е. на обслуживании и в очереди;

U – коэффициент загрузки СМО, показывает, какую часть от общего времени своей работы СМО выполняет обслуживание заявок (значения U < 0,75 указывают, что СМО простаивает значительную часть времени, т.е. используется нерационально, U > 0,85 указывают на перегрузку).

U = ρ(1 – P_отк),  

где ρ - нагрузка на СМО:

 где    .

8. Вероятность отказа в обслуживании:

,

где К^отк – число заявок, получивших отказ в обслуживании;

К – общее число поступивших заявок в СМО.

9. Расчёт относительной пропускной способности:

.

10. Расчёт абсолютной пропускной способности:

Q = q ∙ λ .

Эффективность СМО характеризует ее приспособленность к выполнению задач по обслуживанию. Показатель эффективности – количественная мера эффективности, определяющая степень состояния результатов функционирования СМО целям (задачам), стоящим перед системой. [2]

2. Получение результатов при моделировании

С помощью программы осуществляем одну реализацию (прогон) работы парикмахерской по заданным параметрам (таб. 1).

Таблица1.

В системе обслуживания возможны события двух типов: поступление клиентов или их уход . (таб. 2)

Событие, связанное с поступлением клиента

1. Генерация момента времени, в который поступает следующее требование на обслуживание, путём вычисления промежутка времени между требованиями и добавления его к текущему времени моделирования.

2. Проверка состояния системы

- если система простаивает, то начать обслуживание поступившего клиента, сгенерировать время обслуживания и вычислить время окончания обслуживания, изменить состояние системы и канала на рабочее.

- если система работает, поставить поступившего клиента в очередь и увеличить ее длину на единицу ( если в очереди есть место, в противном случае заявке отказывают в обслуживании).

Событие, связанное с окончанием обслуживания:

1. Проверка состояния очереди

- если очередь пуста, объявить простой системы.

- если, непуста, то начать обслуживание первого по очереди клиента, уменьшить длину очереди, получить время обслуживания клиента и вычислить время окончания обслуживания.[1]

Таблица2.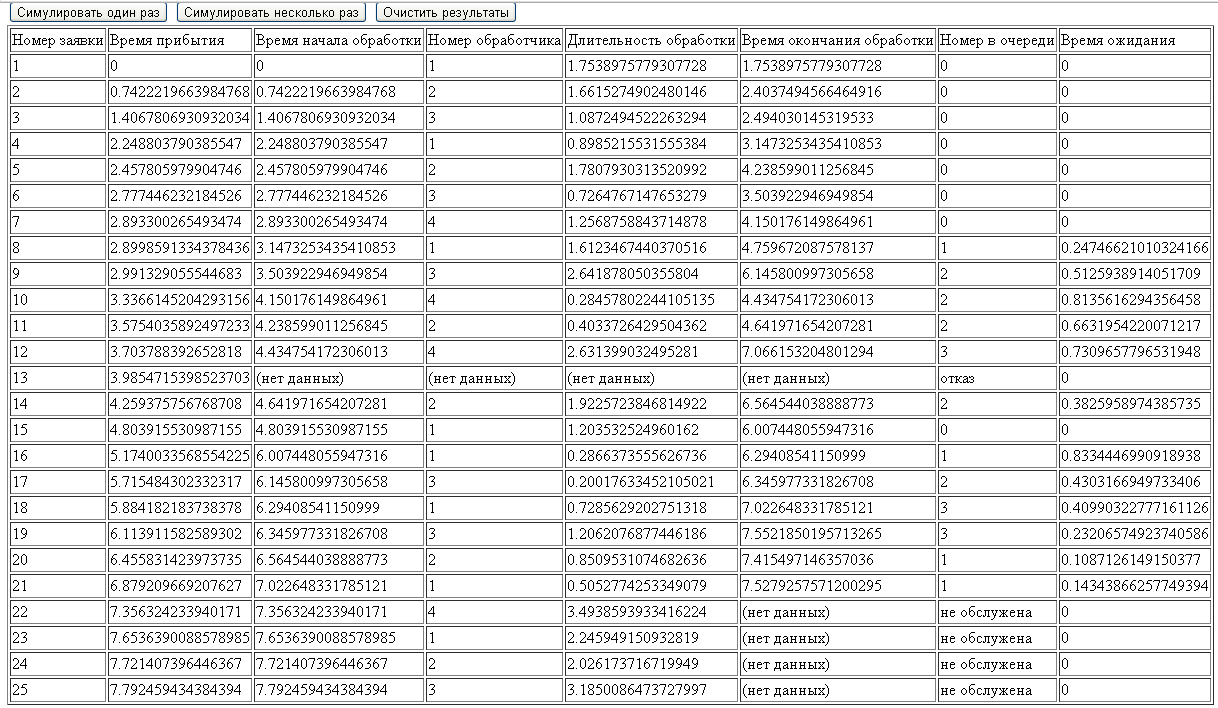

Вывод:

Вероятность того, что в произвольный момент времени длина очереди равна 0: 0.6042202783458432 Вероятность того, что в произвольный момент времени длина очереди равна 1: 0.17821976399927686 Вероятность того, что в произвольный момент времени длина очереди равна 2: 0.1423670771377003 Вероятность того, что в произвольный момент времени длина очереди равна 3: 0.07519288051717965 Среднее время ожидания: 0.22033041914438925 Вероятность отказа : 0.04 Относительная пропускная способность : 0.96 Абсолютная пропускная способность: 2.88 Средняя длина очереди: 2