2.2.Опытные законы идеального газа

Закон Бойля-Мариотта: при T=const, m=const pV = const (изотермический процесс , рис.1).

Закон Гей-Люссака: при p=const, m=const V=V_oaT (изобарный процесс , рис.2), при V=const, m=const p=p_oaT (изохорный процесс , рис.3).

Закон Авогадро: моль любого газа при одинаковой температуре и давлении занимает одинаковый объем V_m (при нормальных условиях V_m = 22.41^.10^-3 м³).

Закон Дальтона: давление смеси газов равно сумме парциальных давлений р₁, р₂,... р_n входящих в нее газов p = p₁+p₂+...+p_n. Парциальное давление - давление, которое производил бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре.

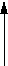
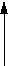
p V p

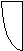
T₂ p₂ V₂

T1<T2 p₁>p₂ V₁>V₂

T₁ p₁ V₁

V T T

Рис.1. Рис.2. Рис.3.

2.3.Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)

Функциональная связь между давлением, объемом и температурой называется уравнением состояния. Для идеального газа, используя законы Бойля-Мариотта, Гей-Люссака и Авогадро, можно получить:

уравнение Клапейрона-Менделеева для одного моля газа pV_m = RT, (1a)

где R = 8.31 Дж/моль^.К - газовая постоянная (она находится после подстановки в последнее уравнение нормальных условий)

уравнение Клапейрона-Менделеева для произвольной массы газа pV =(m/M)RT = nRT, (1b)

где М - масса одного моля (молярная масса), n = m/M - количество вещества.

Можно ввести постоянную Больцмана k = R/N_A = 1.38^.10^-23 Дж/К и тогда уравнение Клапейрона-Менделеева имеет вид p = nkT, (1c)

где n = N_A/V_m - число молекул в единице объема (концентрация молекул), т.е. при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул (в 1 м³ при нормальных условиях содержится N_L = 2.68^.10²⁵ молекул - число Лошмидта).

2.4.Основное уравнение молекулярно-кинетической теории идеальных газов выводится в предположении, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие.

p = (1/3)nm<v_кв>², (2)

где n = N/V - концентрация молекул газа, N - число молекул газа, V - объем газа, <v_кв> = [(1/N)v_i²]^1/2 - среднеквадратичная скорость молекул, v_i - скорость i-молекулы, m - масса одной молекулы.

Суммарная кинетическая энергия поступательного движения всех молекул газа E = N[m<v_кв>²/2] и, следовательно, уравнение (2) можно записать pV = (2/3)E.

Если сравнить уравнение (2) с уравнением Клапейрона-Менделеева (1), то можно получить выражения для среднеквадратичной скорости молекул <v_кв> = (3a)

и для средней кинетической энергии поступательного движения одной молекулы идеального газа

<E_k> = 3kT/2. (4)

Таким образом, термодинамическая температура Т является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (4) раскрывает молекулярно-кинетическое толкование температуры.