8. Сравнение двух вариантов системы (централизованной и децентрализованной) с использованием:

8.1. Векторные методы оптимизации (количественные методы выбора наилучшей альтернативы)

При появлении многокритериальных задач возникли дополнительные трудности их решения, связанные с получением информации от ЛПР [4]. Естественной реакцией на это было стремление получить такую информацию сразу и быстро устранить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так называемых весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле:

,

где -частные критерии, а 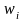- веса критериев.

Определим оценки весов по численной шкале 1-100 для пяти критериев:

1. Время регулирования - .

2) Время нарастания - .

3) Время от начала процесса до первого момента достижения установившегося значения - .

4) Перерегулирование - .

5) Максимальный отклик - .

Нормируем дынные оценки весов, разделив каждый вес на сумму всех:

.

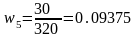
Теперь умножим полученные веса на каждый соответствующий критерий и просуммируем полученные числа:

w=[0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375 0.28125 0.125 0.21875 0.28125 0.09375]

vect1=[5.22; 1.14; 2.76; 8.15; -5.96; 6.83; 0; 1.68; 42.1; -1.21; 4.02; 1.89; 3.54; 3.45; -21.5; 4.49; 0.798; 2.37; 28.3; -18.9; 7.08; 0.11; 0.598; 103; -12.4]

vect2=[11.6; 0.936; 3.07; 37.8; -13.5; 14.3; 0; 2.23; 11.1; -5.31; 12.2; 0.988; 3.73; 48; -43.5; 14; 0.686; 3.07; 148; -32.8; 14.6; 0.458; 2.48; 415; -20.9]

vect11=[4.76; 2.78; 7.22; 0.158; -0.5; 6.94; 0; 1.83; 51.2; -1.9; 5.29; 3 14; 0.01; -15.7; 5.29 ;1.62; 2.89 ;8.03; -15.7 ;6.05; 0.277; 1.97 ;43; -11.7];

vect21=[14.8; 0.42; 3.09; 139 ;-19.1; 15.5 ;0 ;2.4 ;4 ;-10.6; 6.44 ;3.13; 7.41 ;1.11; -33 ;9.47; 1.16 ;4.44 ;12.6 ;-31.7 ;13.4 ;0.491; 1.43 ;69.4; -20.3].

kr1=w*vect1

kr11=w*vect11

kr2=w*vect2

kr21=w*vect21

Для первого генератора получили:

Для децентрализованной системы:

kr1 = 57.0699

Для централизованной системы:

kr11 = 39.5666

Для второго генератора получили:

Для децентрализованной системы:

kr2 = 197.0532

Для централизованной системы:

kr21 = 74.3617

Для двух генераторов оценки для централизованной системы получились меньше, что свидетельствует о более качественной централизованной системе (так как все оценки чем больше, тем хуже качество системы).

8.2. Вербальные методы анализа

Метод ЗАПРОС.

Метод Замкнутых Процедур Опорных Ситуаций применяется для упорядочения многокритериальных альтернатив [4].

Постановка задачи.

Дано:

1. - множество критериев с порядковыми шкалами.

2. - число оценок по шкале критерия .

3. - шкала критерия , - вербальные оценки по критерию.

4. - множество векторных оценок вида

5. - множество векторных оценок, описывающих реальные альтернативы.

Требуется: построить упорядочение многокритериальных альтернатив (множества А) на основе предпочтения ЛПР.

Таким образом, есть 2 альтернативы – централизованная и децентрализованная система (для 1 и для 2 генератора).

Векторные критерии для децентрализованной системы:

vect1=[5.22 1.14 2.76 8.15 -5.96 6.83 0 1.68 42.1 -1.21 4.02 1.89 3.54 3.45 -21.5 4.49 0.798 2.37 28.3 -18.9 7.08 0.11 0.598 103 -12.4]

vect2=[11.6 0.936 3.07 37.8 -13.5 14.3 0 2.23 11.1 -5.31 12.2 0.988 3.73 48 -43.5 14 0.686 3.07 148 -32.8 14.6 0.458 2.48 415 -20.9]

Векторные критерии для централизованной системы:

vect1=[4.76 2.78 7.22 0.158 -0.5 6.94 0 1.83 51.2 -1.9 5.29 3 14 0.01 -15.7 5.29 1.62 2.89 8.03 -15.7 6.05 0.277 1.97 43 -11.7];

vect2=[14.8 0.42 3.09 139 -19.1 15.5 0 2.4 4 -10.6 6.44 3.13 7.41 1.11 -33 9.47 1.16 4.44 12.6 -31.7 13.4 0.491 1.43 69.4 -20.3].

Было выделено 5 критериев оценки систем:

1. Время регулирования.

2) Время нарастания.

3) Время от начала процесса до первого момента достижения установившегося значения.

4) Перерегулирование.

5) Максимальный отклик.

Время регулирования (f₁). Шкала состоит из 2-х оценок (N₁=2):

1) маленький промежуток времени

2) большой промежуток времени

Время нарастания (f₂). Шкала состоит из 2-х оценок (N₂=2):

1) маленький промежуток времени

2) большой промежуток времени

Время от начала процесса до первого момента достижения установившегося значения. (f₃). Шкала состоит из 2-х оценок (N₃=2):

1) маленький промежуток времени

2) большой промежуток времени

Перерегулирование. (f₄). Шкала состоит из 2-х оценок (N₄=2):

1) маленькое

2) высокое

Максимальный отклик. (f₅). Шкала состоит из 2-х оценок (N₅=2):

1) маленький

2) высокий

Множество A будет состоять из векторных оценок сравниваемых проектов, например: a⁽ⁱ⁾ = (маленький промежуток времени, большой промежуток времени, большой промежуток времени, маленькое, высокий).

Метод ЗАПРОС в данном случае может быть применен для упорядочивания сравниваемых вариантов по предпочтительности с учетом заданных критериев, после чего уже будет осуществлен отбор наиболее предпочтительной системы/

Основная идея метода ЗАПРОС заключается в том, что ЛПР предлагается сравнивать не реальные альтернативы (векторные оценки из множества A), а некоторые гипотетические варианты (их векторные оценки из множества Y).

Заданы пять критериев, у каждого шкала с двумя оценками.

Построим оценки для всех пяти графиков.

У первой альтернативы список векторных оценок будет иметь вид:

Для 1 генератора:

L₁₁ = { (1,0,1,0,0),(1,1,1,0,1),(0,1,0,0,0),(0,1,0,0,0),(0,0,1,0,0) }.

Для 2 генератора:

L₁₂ = { (1,0,0,1,0),(0,0,0,0,0),(0,1,1,0,1),(0,1,0,0,1),(1,0,0,0,1) }.

У второй альтернативы:

Для 1 генератора:

L₂₁ = { (1,1,0,1,1),(1,1,1,0,1),(0,0,1,1,1),(0,0,0,1,0),(0,0,0,1,0) }.

Для 2 генератора:

L₂₂ = { (1,1,0,0,0),(0,0,0,1,1),(1,0,0,1,1),(1,0,0,1,1),(1,0,1,1,1) }.

Представим полученные оценки в виде:

L= {(оценки по 1 критерию),(оценки по 2 критерию),(оценки по 3 критерию),(оценки по 4 критерию),(оценки по 5 критерию) }.

У первой альтернативы список векторных оценок будет иметь вид:

Для 1 генератора:

L₁₁ = { (1,1,0,0,0),(0,1,1,1,0),(1,1,0,0,1),(0,0,0,0,0),(0,1,0,0,0) }.

Для 2 генератора:

L₁₂ = { (1,0,0,0,1),(0,0,1,1,0),(0,0,1,0,0),(1,0,0,0,0),(0,0,1,1,1) }.

У второй альтернативы:

Для 1 генератора:

L₂₁ = { (1,1,0,0,0),(1.1,0,0,0,),(0,1,1,0,0),(1,0,1,1,1),(1,1,1,0,0) }.

Для 2 генератора:

L₂₂ = { (1,0,1,1,1),(1,0,0,0,0),(0,0,0,0,1),(0,1,1,1,1),(0,1,1,1,1) }.

Данные можно объединить в общий критерий (1 для 5 графиков).

У первой альтернативы список векторных оценок будет иметь вид:

Для 1 генератора:

L₁₁ = { 0,1,1,0,0 }.

Для 2 генератора:

L₁₂ = { 0,0,0,0,1 }.

У второй альтернативы:

Для 1 генератора:

L₂₁ = { 0,0,0,1,1 }.

Для 2 генератора:

L₂₂ = { 1,0,0,1,1 }.

Полученные пары предъявляются ЛПР для сравнения.

Будем задавать вопросы, подобные этим:

Вопрос. Что вы предпочитаете: систему с большим временем регулирования или большим временем нарастания?

Ответ ЛПР. Систему с большим временем нарастания.

Вопрос. Что вы предпочитаете: систему с большим временем нарастания или большим перерегулированием?

Ответ ЛПР. Систему с большим временем нарастания.

Пусть АБВГД – оценки по критериям.

А₁Б₁В₁Г₁Д₁ – оценки для первой альтернативы.

А₂Б₂В₂Г₂Д₂ – оценки для второй альтернативы.

Будем сравнивать оценки попарно, выступая в роли ЛПР.

Для первого генератора:

АБ -> Б₁ (то есть выбираем из А_1, Б_1, А_{2 ,}Б₂ )

АВ -> В₁

АГ -> Г₂

АД -> Д₂

БВ-> Б₁

БГ-> Г₂

БД -> Д₂

ВГ-> Г₂

ВД-> Д₂

ГД-> Д₂

Таким образом, выберем наилучшие оценки - Г₂, Д₂, из чего следует, что вторая альтернатива (централизованная система для 1 генератора) лучше.

Для второго генератора:

АБ -> A₂

АВ -> A₂

АГ -> А₂

АД -> А₂

БВ-> Б₁

БГ-> Г₂

БД -> Д₂

ВГ-> Г₂

ВД-> Д₂

ГД-> Г₁

Таким образом, выберем наилучшие оценки - А₂, Г₂, Д₂, из чего следует, что вторая альтернатива (централизованная система для 2 генератора) лучше.