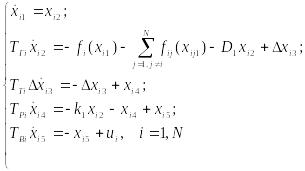ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ

КАФЕДРА «СИСТЕМНЫЙ АНАЛИЗ И УПРАВЛЕНИЕ»

Курсовая работа

по предмету «Современные проблемы системного анализа и управления»

на тему «Построение системы синтеза управлений, обеспечивающих требуемое качество переходных процессов в системе параллельно работающих синхронных генераторов»

выполнила:

студентка группы № 6082/11

Пряхина М.А.

проверил:

проф. Шашихин В.Н.

Санкт-Петербург

2012. г.

Содержание

1. Постановка задачи 3

2. Декомпозиция системы на подсистемы. Проверка управляемости подсистемы 5

3. Синтез управления с заданной структурой и свойствами с проверкой условий разрешимости 6

4. Формирование замкнутой системы и построение системы сравнения 10

5. Проверка устойчивости системы сравнения 12

6. Построение переходных процессов по Х про заданном Хо 14

7. Выбор векторного критерия качества замкнутой системы из пяти компонентов 17

8. Сравнение двух вариантов системы (централизованной и децентрализованной) с использованием: 20

8.1. Векторные методы оптимизации (количественные методы выбора наилучшей альтернативы) 20

8.2. Вербальные методы анализа 22

ЗАКЛЮЧЕНИЕ 28

Список литературы 29

ПРИЛОЖЕНИЕ 30

1. Постановка задачи

Рассмотрим систему синтеза управлений, которые должны обеспечивать требуемое качество переходных процессов в системе параллельно работающих синхронных генераторов.

(1)

Здесь - угол поворота ротора i-го СГ относительно синхронной оси вращения,

- скольжение i-го СГ (угловая скорость вращения),

- механическая мощность, подводимая от i-го ТА,

- уставка регулятора i-го ТА,

- положение регулятора скорости i-го ТА,

- сигнал вторичного регулятора скорости,

- управляющее воздействие,

нелинейная функция характеризует мощность, генерируемую i-ым СГ,

а функция – мощность, передаваемую от i-го СГ к j-ому СГ,

-коэффициент демпфирования,

- постоянные инерции СГ, ТА, вторичного регулятора скорости соответственно,

- производная по времени.

Система децентрализованная. Необходимо синтезировать оптимальное управление.

Приведем систему к более наглядному виду.

(2)

Найдем матричные параметры А,В,С системы в пространстве состояний вида:

(3)

; ;

;

;

;

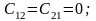
2. Декомпозиция системы на подсистемы. Проверка управляемости подсистемы

Проверим управляемость полученной системы с помощью теоремы Калмана – критерия управляемости.

Объект вполне управляем тогда и только тогда, когда ранг матрицы управляемости равен размерности вектора состояния x.

Для децентрализованной системы имеем:

,

где -медианная матрица.

Собственные числа матрицы :

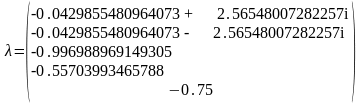
В среде Matlab получим матрицу управляемости:

A_n=[0 1 0 0 0;-7.8 -0.168 30 0 0; 0 0 -0.9 0.6 0; 0 -0.016 0 -0.9 0.6;0 0 0 0 -0.9];

A_v=[0 1 0 0 0;-5.2 -0.112 45 0 0; 0 0 -0.6 0.9 0; 0 -0.016 0 -0.6 0.9;0 0 0 0 -0.6];

B=[0;0;0;0;0.75];

for i=1:1:5

for j=1:1:5

A_med(i,j)=[A_n(i,j)+A_v(i,j)]/2;

end; end

Sy=[B A_med*B A_med^2*B A_med^3*B A_med^4*B]

В среде Matlab проверим ранг матрицы управляемости

rang=rank(Sy)

Ранг матрицы управляемости равен 5, что свидетельствует об управляемости системы.

3. Синтез управления с заданной структурой и свойствами с проверкой условий разрешимости

Система имеет полностью децентрализованную по входам структуру, состоящую из N взаимодействующих подсистем:

(4)

где - вектор фазовых координат i-ой подсистемы; - вектор управляющих воздействий; - векторная функция, характеризующая влияние на i-ую подсистему всех остальных систем.

Требуется синтезировать управление в виде обратной связи

(5)

которое обеспечивает асимптотическую устойчивость системы и минимизирует функционал

(6)

- блочная матрица, элементы которой определяются в процессе синтеза.

Определение параметров управления, оптимизирующего данный функционал, требует решения уравнения Риккати

(7)

где

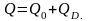
Для построения децентрализованного управления и уменьшения вычислительных затрат при проектировании матрица Р должна иметь диагональную структуру. Выполним тождественные преобразования уравнения (7), которые приведут его к диагональной структуре решения. В силу представления матриц в виде суммы двух матриц 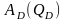и блочно-недиагональной 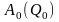уравнение (7) преобразуется к уравнению Риккати

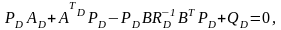(8)

и уравнению для взаимосвязей между подсистемами

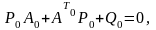(9)

Так как матрицы имеют блочно-диагональную структуру, то матрица будет иметь аналогичную структуру и уравнение (8) эквивалентно N «расщепленным» уравнениям Риккати меньшей размерности

(10)

а оптимальное стабилизирующее управление принимает искомую децентрализованную структуру

(11.а)

или

(11.б)

где - решение уравнения Риккати, которое соответствует i-ой подсистеме,

Отрицательная обратная связь (11) является решением задачи линейно-квадратичной оптимизации функционала (6) при динамических ограничениях (4). Блочные элементы матрицы находятся из соотношения (9), которое может быть представлено в виде N уравнений:

(12)

Для интервальных матриц решим два уравнения Риккати (верхнее и нижнее):

Возьмём _, матрицу как единичную.

Теперь необходимо найти матрицы из алгебраического уравнения Риккати.

Уравнения Риккати решим в Matlab:

A_n=[0 1 0 0 0;-7.8 -0.168 30 0 0; 0 0 -0.9 0.6 0; 0 -0.016 0 -0.9 0.6;0 0 0 0 -0.9];

A_v=[0 1 0 0 0;-5.2 -0.112 45 0 0; 0 0 -0.6 0.9 0; 0 -0.016 0 -0.6 0.9;0 0 0 0 -0.6];

B=[0;0;0;0;0.75];

Q=eye(5)

R=1

[K,P,Lam]=lqr(A_n,B,Q,R)

[K2,P2,Lam2]=lqr(A_v,B,Q,R)

Получили следующие параметры регулятора: