§ 3. Тригонометрические функции числового аргумента

Абсцисса X точки М_а числовой единичной окружности (рис. 38) называется косинусом числа а:

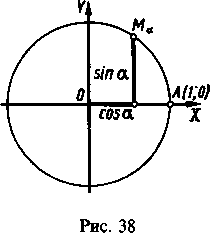JT=cosa. (9.12)

Ордината Y точки М_а числовой единичной окружности называется синусом числа а:

r=sina. (9.13)

Областью определения косинуса и синуса служит множество всех действительных чисел, т. е. D (cos a) = R, D (sin a) = R.

Отношение синуса числа a к его косинусу называется тангенсом числа а:

tg а=sin a/cos а. (9.14)

Область определения тангенса—множество всех действительных чисел, за исключением чисел вида %/2 + nk, ке Z.

Отношение косинуса числа а к его синусу называется котангенсом числа а:

ctg а=cos a/sin а. (9.15)

Область определения котангенса—множество всех действительных чисел, за исключением чисел вида nk, кеZ.

Величина, обратная косинусу числа а, называется секансом числа а:

sec а= 1/cos а. (9.16)

Область определения секанса—множество всех действительных чисел, за исключением чисел вида %/2 + кк, кеZ.

Величина, обратная синусу числа а, называется косекансом числа а:

(9.17)

cosec а = 1/sin а.

Область определения косеканса—множество всех действительных чисел, за исключением чисел вида nk, ке Z.

При решении задач тригонометрические функции рассматриваются или как функции числа, или как функции дуги (угла), заданные на множестве всех действительных чисел или на множестве всех дуг (углов). При этом каждому действительному числу или каждой дуге (углу) соответствует единственное значение тригонометрической функции.

Функции cos а и sin а ограничены, так как — l<£(cosa)<l и

• 1<Е (sin a)< 1.

Функции tga и ctga не ограничены, так как каждая из них может принимать любое действительное значение, т. е. Е (tg a) = R и Е(ctga) = R.

38. Могут ли синус и косинус быть равными: 1) 0,85; 2) 7/6;

3. -ХД/у/3; 4) -1,01; 5) 3/У10; 6) Уш/я; 7) а/^а²+Ь², а>0, Ь>0; 8) а/у/а²—b², a>0, \b\<al

38. Могут ли синус, косинус, тангенс и котангенс принимать значение, равное: 1) 1/2; 2) yjl\ 3) —5,1; 4) >/0^; 5) 2,2; 6) у/3/21

39. Могут ли функции sin a, cos a, tga, ctga принимать отрицательные значения, если а выражает величину угла тре­угольника?

40. Чем отличаются друг от друга области определения sin a и tga?

41. Сравните абсолютную величину тангенса любого числа с абсолютной величиной синуса этого числа.

42. Какие множества значений имеют функции sin a, cos а, tga и ctga?

43. Найдите значения а в промежутке 0^а<2я, для которых выполняется равенство: 1) sina=0; 2) sina=l; 3) sina= —1;

3. cosa = 0; 5) cosa=l; 6) cosa= — 1.

38. Найдите значения a в промежутке 0<а<2я, для которых выполняется равенство: 1) tga=0; 2) tga= 1; 3) tga= — 1; 4) ctga=0;

3. ctga=l; 6) ctg a= — 1.

§ 4. Знаки, числовые значения и свойства четности и нечетности тригонометрических функций

Функция y=f(x) называется четной, если при всех значениях х и об­ласти определения этой функции /(—x)=f(x).

Функция y=f(x) называется нечетной, если при всех значениях х из об­ласти определения этой функции /(—х)= —f (х).

Свойства четности и нечетности тригонометрических функций выража­ются следующими формулами:

sin(—a)= —sin a; cos(—a) = cos a; tg(-a)=-tga; ctg(—a)= -ctga.

(9.18)

(9.19)

(9.20)

(9.21)

Четверть Функция	I 0<а<я/2	II 7t/2<a<7t	Ill , гс<а<Зя/2	IV Зя/2<а<2гс
sin a	+	+	-	-
cos a	+	-	-	+
tga	+	-	+	-
ctga	+	—	+	-

Знаки тригонометрических функций по четвертям приведены в табл. III.

Значения тригонометрических функций некоторых дуг (углов) приведены в табл. IV.

38. Какие знаки имеют: 1) cos 150°; 2) sin 320°; 3) tg220°;

ctg400°?

О 1) 90° < 150° < 180° (II четверть); cosl50°<0;

2. 270° <320° <360° (IV четверть); sin 320° <0;

3. 180° <220° <270° (III четверть); tg220°>0;

4. 360° <400° <360°+ 90° (I четверть); ctg400°>0. #

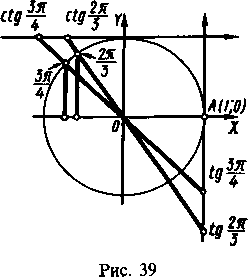38. Используя единичную окружность, определить знаки раз­ностей: 1) sin (27с/3) — sin (Зте/4); 2) cos(2tc/3)—cos(3ti/4); 3) tg(2Ti/3) — -tg(Зтс/4); 4) ctg(2тс/3) ctg(Зя/4).

О 1) Сравнивая ординаты концов дуг 2я/3 и Зтс/4, находим sin (27с/3) — sin (Зте/4) > 0 (рис. 39).

2. Сравнивая абсциссы концов дуг 2я/3 и Зтс/4, получим cos (2я/3)—cos (Зтс/4) >0.

3. Сравнивая ординаты точек на оси тангенсов, имеем tg (2те/3)—tg (Зтс/4) < 0.

4. Сравнивая абсциссы точек на оси котангенсов, получим ctg (2я/3) —

—ctg (Зте/4) > 0. ф