§ 5. Исследования на экстремум в задачах на площади поверхностей фигур вращения

35. Из всех цилиндров, вписанных в данный конус с радиусом основания R и высотой Я, найти тот, у которого площадь боковой поверхности наибольшая.

О Пусть г—радиус основания искомого цилиндра, a h—его высо­та (см. рис. 168). Из подобия треугольников ABO_t и СВО имеем R/r=H/(H—h), откуда r=R(H—h)/H. Подставив значение г в формулу площади боковой поверхности цилиндра S=2nrh, получим

S=2nh^^~——, или S=^^(Hh—h²) (0<h<H).

Я Я

Исследуем функцию на экстремум с помощью второй производной: Г.Щи-Щ Я-й-0; A-f; S'—

Вторая производная отрицательна, следовательно, функция при h = H/2 имеет максимум.

R(H—H/2) R

Найдем радиус основания искомого цилиндра: г=—-—— ф

Я 2

36. Из всех цилиндров, вписанных в данный конус (R и Н даны), найдите тот, у которого площадь полной поверхности наибольшая.

37. Из всех цилиндров данного объема V найдите тот, у которого площадь полной поверхности наименьшая.

38. Найдите радиус основания и высоту цилиндрического бака с наименьшей площадью поверхности (без крышки) при заданном объеме V.

39. Из всех конусов с данной площадью боко­вой поверхности S найти тот, у которого объем наибольший.

40. 

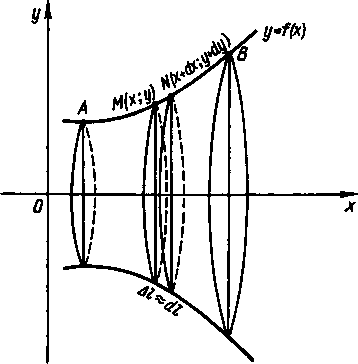
    Рис. 177

    Из всех цилиндров, вписанных в шар радиуса R, найдите тот, у которо­го площадь боковой по­верхности наибольшая.

41. Найдите радиус ос­нования и высоту цилинд­рического бака (без крыш­ки) наибольшего объема при заданной площади по­верхности S.

42. Из всех цилиндров с данной площадью пол­ной поверхности S найди­те тот, у которого объем наибольший.

43. Из всех конусов, вписанных в шар радиуса R, найдите тот, у которого площадь боковой поверхности наибольшая.

§ 6. Вычисление площадей поверхностей фигур вращения с помощью определенного интеграла

При вращении дуги АВ плоской кривой y=f(x) вокруг оси Ох образуется поверхность вращения (рис. 177).

Дифференциал площади dS этой поверхности равен площади боковой поверхности кругового усеченного конуса с радиусами оснований у и y+dy и образующей dl:

Klnydl

(слагаемым dy можно пренебречь ввиду его малости по сравнению с 2у).

Площадь поверхности, образованной вращением дуги А В вокруг оси Ох, вычисляется по формуле

ъ ъ ъ .

S=j*</S=27ij*j/d/=27ij*j, / 1+^^ dx, (26.9)

а а а

где а и b—значения независимой переменной х в точках А и В.

Аналогичным образом, при вращении дуги АВ вокруг оси Оу имеем dSttlnxdl, откуда

d d .

S=2jtJ'jt<//=27tj'* I l+^~J dy, (26.10)

где с и d—значения независимой переменной у в точках А и В.

44. Найти площадь поверхности шара, образованного враще­нием окружности х²+у² = г² вокруг оси Ох.

О Дифференцируя уравнение окружности х² +у² = г², получим 2x4-

dy dy х + 2у—=0, —=—. Найдем дифференциал дуги: dx dx у

dl= /1 +

Подставив значение дифференциала dl в формулу (26.9) и взяв пределы интегрирования от —г до г, получим

= 471 г².

S=2п J у^Г-^-=2ш j* dx=2nrx

45. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги окружности (х—4)²+у² = 36, заключенной между точками А(2\4yjl) и В(4; 6).

О Дифференцируя уравнение окружности по х, получим Следовательно,

⁵’²*Ы¹⁺(л) *■

4

= 24тс (кв. ед.).

2

2

4

= 2п J^/36 —(х—4)²+(х—4)² dx= \2п\dx= \2пх

46. Найдите площадь поверхности шарового пояса с высотой Я, образованного вращением дуги окружности х²-\-у² = г² вокруг оси Ох (рис. 178).

47. Найдите площадь поверхности шарового сегмента с высотой #, образованного вращением дуги окружности х²+у² = г² вокруг оси Ох (рис. 179).

48. Найдите площадь поверхности шарового пояса, образован­ного вращением вокруг оси Ох дуги окружности х²+у²= 16, заключенной между точками А(2;2у/3) и Б(3; yfl).

49. Найдите площадь поверхности шарового пояса, образован­ного вращением вокруг оси Оу дуги окружности лс²+>>² = 25, заключенной между точками А (4; —3) и #(3; 4).

50. Найдите площадь поверхности, образованной вращением вокруг оси Оу дуги окружности х²+(у—2)² = 25, заключенной между точками А(2^/б; 1) и В(4; 5).

51. Вычислите площадь поверхности, образованной вращением вокруг оси Ох дуги параболы у² = 4х, ограниченной точками 0(0; 0) и А(3;2^3).

52. Вычислите площадь поверхности, образованной вращением вокруг оси Ох дуги параболы у² = 9х, ограниченной точками (0; 0) и (4; 6).