5.7 Точки перегиба.

Определение. Точка называется точкой перегиба функции , если она отделяет участок, где функция выпукла от участка, где функция вогнута.

Рассмотрим, как выглядит на графике точка перегиба. Пусть левее точки функция выпукла, а правее  вогнута. Тогда левее точки график функции лежит над касательной, а правее  под касательной. Точка перегиба характеризуется тем, что здесь кривая переходит с одной стороны касательной на другую ее сторону, то есть кривая пересекает касательную. То же самое будет, если левее функция вогнута, а правее  выпукла.

Точки перегиба являются характерными точками графика функции, и их нахождение является одной из процедур исследования графика.

Необходимое условие точки перегиба

Будем считать, что у существует и непрерывна вторая производная .

Пусть  точка перегиба. Предположим, для определенности, что левее выпукла, а правее вогнута. Тогда левее . Делая предельный переход при , получим

.

Правее функция вогнута, так что . Делая предельный переход при , получим

.

Совместить оба этих неравенства можно только в том случае, если . Это условие и является необходимым условием точки перегиба.

Достаточное условие точки перегиба

Пусть в некоторой точке выполнено условие . Это, конечно, не означает, что есть точка перегиба; это дает лишь точку «подозрительную» на перегиб.

Рассмотрим сразу общую ситуацию. Пусть в точке имеет место условие

.

Возможны два случая

А. , то есть первая по старшинству (порядка выше второго) производная, отличная от нуля, имеет нечетный порядок.

Тогда разложение функции ряд Тейлора имеет вид

а разложение в ряд Тейлора производной имеет вид

.

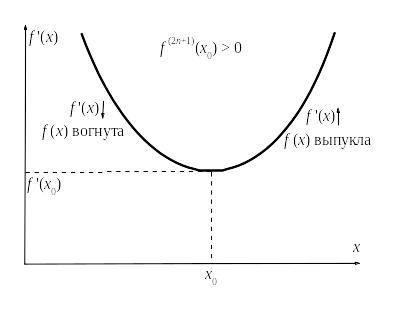
Посмотрим, как выглядит график (обратите внимание: строится график производной , а не самой функции). Так как у четная степень то этот график имеет такой вид:

Пусть . Тогда левее монотонно убывает, а правее монотонно возрастает. Следовательно, левее вогнута, а правее  выпукла и есть точка перегиба функции .

Если же , то левее монотонно возрастает, и там выпукла, а правее монотонно убывает и там вогнута. Следовательно, есть точка перегиба функции .

Б. , то есть первая по старшинству (порядка выше второго) производная, отличная от нуля, имеет четный порядок.

Тогда разложение в ряд Тейлора имеет вид

а разложение в ряд Тейлора производной имеет вид

Снова представим себе, как выглядит график производной (именно производной а не функции!). Так как у нечетная степень, то этот график имеет такой вид:

Пусть . Тогда и левее и правее монотонно возрастает и, следовательно, и левее и правее выпукла.

Если же то и левее и правее монотонно убывает и, следовательно, и левее и правее вогнута. Поэтому в точке перегиба нет.

Таким образом, есть в перегиб или нет, определяется порядком первой по старшинству (порядка выше второго) производной, отличной от нуля. Если это производная нечетного порядка, то есть точка перегиба , если четного порядка  то в перегиба нет.

Схема исследования функции на выпуклость - вогнутость

1. Найти те точки , в которых . Это будут точки «подозрительные» на перегиб.

2. В этих точках найти первую по порядку старшинства (порядка выше второго) производную, отличную от нуля. Если это будет производная нечетного порядка, то является точкой перегиба, если четного  то в перегиба нет.

3. Вычислить значения в точках правее и левее точек перегиба и установить, где функция выпукла, а где вогнута (там, где функция выпукла, а где  вогнута).