4.7 Формула Тейлора.
Формула Тейлора для полинома
Пусть имеется
полином от
степени
:
Сосчитаем все производные от этого полинома до -го порядка включительно:
,
,
,
,
,
.
Положим во всех этих выражениях . Тогда получим
;
;
;
;
;
.
Отсюда получаем
;
;
;
;
.
и поэтому исходный полином может быть записан в виде
.
Для полинома общего вида
=
аналогичным образом можно получить
=
.
Эта формула носит название формулы Тейлора.
Формула Тейлора в общем случае.
Пусть теперь
имеется некоторая произвольная функция
,
у которой в точке
существуют
,
,
,
… ,
.
Для нее тоже можно написать комбинацию
=
,
но теперь, очевидно,
уже нельзя утверждать, что
,
ведь
не полином. Введем, поэтому, функцию
и будем писать
=
.
Функцию будем называть остаточным членом, а саму формулу формулой Тейлора для функции . Самая главная задача теперь сказать что-то о свойствах , а еще лучше как-то оценить его. Тогда можно будет использовать для приближенного вычисления функции .
Свойства остаточного члена.
Напишем в явном виде
=
.
Полагая
,
получим
Далее, находя производные и полагая , получим
=
,
,
=
,
,
=
,
.
Таким образом, остаточный член в формуле Тейлора обладает следующим основным свойством
.
Остаточный член формулы Тейлора в формуле Пеано
Теорема. Пусть
функция
удовлетворяет условию
.
Тогда в окрестности
точки
ее можно представить в виде
,
где
- бесконечно
малая величина, то есть
.
Доказательство этой теоремы проведем по индукции.
1. Рассмотрим случай
.
В этом случае условие теоремы принимает
вид
Так как
,
то, учитывая написанное условие, получим
,
что означает, что
есть бесконечно малая величина. Но тогда
,
что и утверждается в условии теоремы
для
.
2. Пусть теперь
теорема верна для некоторого
.
Докажем, что она верна для
.
Итак, пусть для функции выполнено условие
.
Рассмотрим функцию
.
Для нее будет выполнено условие
.
Так как мы
предположили, что для
теорема верна, то
можно представить в виде
.
Вернемся к . Воспользуемся формулой Лагранжа
,
где
.
Но
,
,
и поэтому
Поделим и умножим
это выражение на
,
где
.
Но при
и поэтому
,
то есть
бесконечно малая величина. Далее, так
как
,
то
и поэтому
.
Как известно, произведение б.м.в. на
ограниченную величину есть также б.м.в..
Поэтому
есть бесконечно малая величина, что и
доказывает нашу теорему.
Следствие. С учетом этой теоремы, формулу Тейлора можно записать в виде
,
где б.м.в., или, в более употребительном виде,
.
Эта формула носит название формулы Тейлора (или ряда Тейлора) с остаточным членом в форме Пеано.
Если взять
то мы получим
,
которая носит название ряда Маклорена с остаточным членом в форме Пеано.
Остаточный член формулы Тейлора в форме Лагранжа
Остаточный член
в форме
дает лишь качественную оценку
.
Хотелось бы иметь более точную
количественную оценку. Такую оценку
часто позволяет получить остаточный
член в форме Лагранжа.
Рассмотрим еще раз выражение для
Рассмотрим функцию
Обратите внимание,
как строиться выражение для функции
:
в выражение для
вместо
ставиться аргумент
.
Очевидно, что
,
Далее вычислим
.
Рассмотрим еще
функцию
.
Для нее
;
;
.
А теперь воспользуемся формулой Коши
,
.
Подставляя сюда соответствующие члены, получим
.
Отсюда получается выражение для остаточного члена :
,
.
Эта форма остаточного
члена и называется остаточным членом
в форме Лагранжа. Ее дальнейшее
использование заключается в том, что
пытаются оценить сверху
,
то есть ищут такое
,
что
.
Тогда
,
что и позволяет оценивать погрешность от использования формулы Тейлора для вычисления . Сама формула Тейлора с остаточным членом в форме Лагранжа имеет вид
,
где . В частном случае
.
Эта формула носит название ряда Маклорена с остаточным членом в форме Лагранжа.
Разложение в ряд Тейлора некоторых функций.
Используя последнюю формулу, напишем разложение в ряд Тейлора некоторых наиболее часто встречающихся функций. Рекомендуется запомнить эти разложения:
А.
.
Пусть
.
Имеем
;
;
;
… ;
;
;
;
;
;
.
Ряд Маклорена дает нам
где
.
Но так как
,
то
и мы имеем оценку
В частности, беря
,
,
получим формулу для вычисления числа
,
где погрешность
не превосходит величины
.
Б.
.
Имеем
;
;
;
;
…
.
Подставляя
,
получим
;
;
;
,
и дальше эти значения начинают повторяться. Поэтому ряд Маклорена дает
,
.
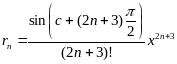Так как
,
то
.
Окончательно
,
.
В.
.
Имеем:
;
;
;
;
… ,
.
Подставляя , получим
;
;
;
и далее эти значения повторяться.
Формула Маклорена дает:
,
.
Так как
,
то
.
Г.
.
Имеем:
;
;
;
;
.
Подставляя , получим
;
;
;
;
;
Подстановка в формулу Маклорена дает
.
Д.
.
Имеем
;
;
;
…
Подставляя , получим
;
;
;
и формула Маклорена дает
.
Заметим, что если
(целое число), то этот ряд обрывается на
,
и получается формула бинома Ньютона.
Данная формула может рассматриваться
как обобщение формулы бинома Ньютона
на случай произвольного вещественного
.