4.5 Теоремы о функциях, имеющих производную
Теорема Ферма
Теорема. Пусть
функция
определена и непрерывна на промежутке
и в некоторой внутренней
точке
этого промежутка достигает своего
наибольшего или наименьшего значения.
Если в этой точке существует производная,
то она равна нулю:
.
Доказательство
Пусть, для определенности, в точке функция достигает своего наибольшего значения.
По условию теоремы
эта точка внутренняя, то есть
,
и поэтому к этой точке можно подойти и
слева и справа.
Пусть мы подходим к слева. Тогда
(так как
наибольшее значение);
;
(так
как мы подходим слева);
;
.
Делая предельный
переход
,
получим
.
Пусть мы подходим к точке справа. Тогда
(так как наибольшее значение);
;
(так
как мы подходим слева);
;
.
Делая предельный переход , получим
.
Совместить два полученных неравенства можно только в одном случае: .
|
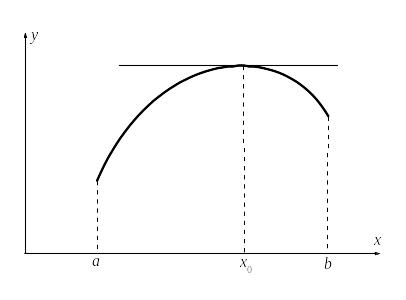
Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX.
|
Существенность ограничений
В теореме Ферма
по сути дела два ограничения: а) точка
расположена внутри отрезка
и б)
.
Покажем, что оба ограничения являются
существенными, то есть отказ от любого
из них приводит к тому, что утверждение
теоремы становится неверным.
а) «внутренность» точки .
|
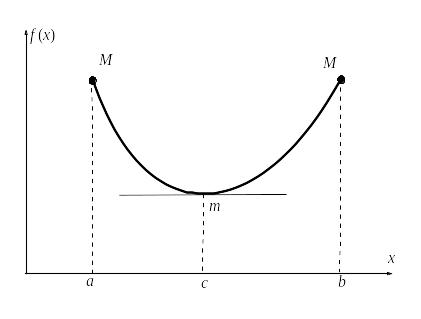
Если максимум или минимум функции достигается на границе отрезка, то, как видно из рисунка, утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке только с одной стороны, и поэтому не получится второго, противоположного неравенства.
|
б) существование производной.
|
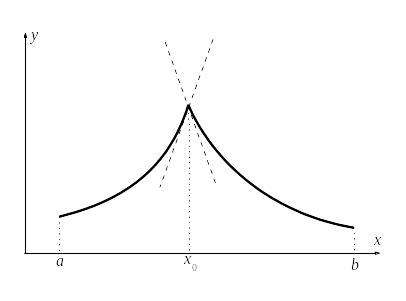
Пусть в точке
существуют только односторонние
производные. Тогда, как это видно из
рисунка, теорема Ферма неверна. При
доказательстве это проявиться в том,
что получаться неравенства
|
и
,
которые нельзя будет объединить в
одно равенство, так как теперь
.
Теорема Ролля
Пусть функция
а) определена и непрерывна на ;
б)
;
в)
Тогда существует
точка
в которой
.
Доказательство этой теоремы следует из такой логической цепочки рассуждений:
1. Так как
определена и непрерывна на
,
то, по первой теореме Вейерштрасса, она
ограничена на
,
то есть существуют конечные
и
.
2. Если
,
то
есть константа, то есть
и поэтому
.
В качестве точки
можно взять любую точку из
.
3.
Если
,
то, в силу условия
и второй теоремы Вейерштрасса, хотя бы
одно из значений
или
достигается во внутренней точке
промежутка
(см. рисунок). По теореме Ферма, в этой
точке (их может быть и несколько)
производная равна нулю.
|
|
Внутри промежутка достигается sup |
Внутри промежутка достигается inf |
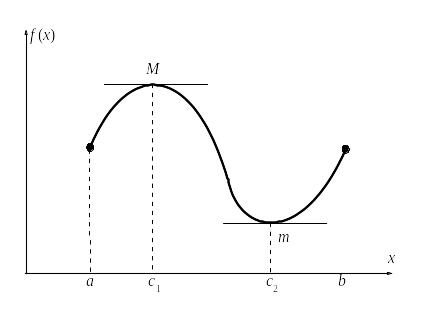
Внутри промежутка достигаются и sup и inf.
Формулы Коши и Лагранжа
Теорема. Пусть
функции
и
а) определены и непрерывны на ;
б)
и
;
в)
.
Тогда существует точка такая, что
.
Эта формула носит название формулы Коши.
Доказательство.
Прежде всего отметим, что
,
иначе, по теореме Ролля, существовала
бы точка
,
где
,
что противоречит ограничению «в».
Рассмотрим функцию
.
Она
а) определена и непрерывна на , так как и функции и непрерывны на ;
б)
.
в)
.
Таким образом, для
выполнены все условия теоремы Ролля.
Поэтому
такая, что
,
но тогда в этой точке
,
что и дает формулу Коши.