Глава 4. Производная

4.1 Определение и геометрический смысл производной

Пусть функция непрерывна в точке .

Определение. Производной от функции в точке называется величина

.

Дадим некоторые расшифровки этого важнейшего понятия математического анализа.

а) Вспоминая определение предела, можно записать определение через кванторы .

б) Величина называется приращением аргумента, а величина приращением функции. Тогда

.

в) Обозначая , можно записать

.

Понятие производной впервые появилось в физике в связи с понятием скорости. Пусть некоторая материальная точка движется по оси так что есть координата точки в момент времени . Спустя время координата точки будет , т.е. за время точка пройдет путь . Поэтому средняя скорость точки за интервал времени будет равна . Чтобы найти мгновенную скорость точки в момент времени надо устремить к нулю, то есть

.

Таким образом, производная от координаты точки определяет ее мгновенную скорость. Поэтому и производную функции в некоторой точке можно трактовать как скорость изменения функции в этой точке.

Дадим еще геометрический смысл производной. В определение производной входят две операции: деление и предельный переход при . Что же это дает? Нанося на график точки с координатами ( , ) и ( , ) мы получим фигуру изображенную на рисунке. Проведем через эти точки линию, которая называется секущей. Тогда дробь есть не что иное как , где есть угол наклона секущей к оси OX.

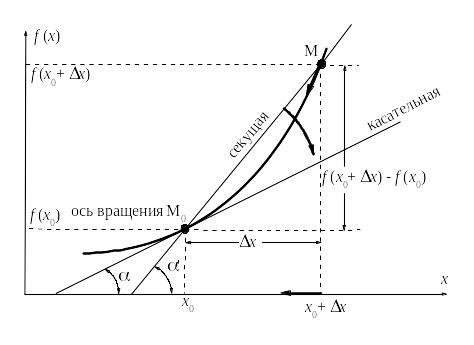
Но в определении производной есть еще предельный переход при . Что же дает этот предельный переход?.

При точка M начинает двигаться к точке M₀. При этом вся секущая будет поворачиваться около точки M₀ и в пределе она превратиться в касательную к точке M₀. Угол при этом перейдет в угол , который эта касательная образует с осью х. Поэтому можно утверждать, что

,

где  угол, образованный касательной к кривой в точке и осью OX.

4.2 Алгебра производных

Выведем важнейшие формулы, касающиеся вычисления производных. В дальнейшем и  некоторые функции, у которых существуют и , а с  некоторая константа (число).

1. .

Доказательство.

.

2. .

Доказательство

Аналогично выводится формула для .

3. .

Доказательство

(В числителе дроби прибавим и вычтем комбинацию )

4.  .

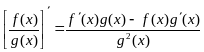Доказательство

(прибавляем и вычитаем в числителе комбинацию )

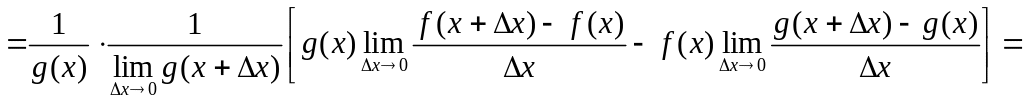
5.  .

В выражении подразумевается, что производная от функции берется так, как будто является единым целым (аргументом).

Доказательство

Пусть аргумент получил приращение . Тогда функция получила приращение так что . Поэтому

(делим и умножаем дробь на )

.

6.

Доказательство

Пусть так что . Если аргументу x дать приращение , то величина получит приращение . Поэтому

=

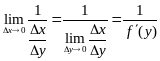
Однако в данной формуле есть одна неувязка. Слева стоит функция от , а справа получилась функция от . Чтобы устранить это несоответствие надо в правой части заменить на . Тогда получим окончательно

.

7.

Вывод этой формулы следует разбирать после прочтения следующего параграфа.

Доказательство

Обозначим . Тогда . Вычисляя производную от обеих частей этого равенства, получим

.

Отсюда

.

Вместо того чтобы запоминать эту формулу лучше запомнить правило: для того чтобы вычислить производную от , надо это выражение сначала прологарифмировать.

Все эти формулы сведены в следующую таблицу, которую следует запомнить (кроме последней формулы).

Таблица 1.

Функция	Производная