Логарифмическая функция Функция, обратная ax, называется логарифмической функцией, и обозначается logax. Ее свойства получаются как следствия свойств функции ax

а) а > 1.

1. Так как. значения ax(0; +), то logax определена для 0<x<+. 2. Так как ax строго монотонно возрастает, то logax тоже строго монотонно возрастает. 3. Так как ax непрерывна, то и logax тоже непрерывна. 4.  . называется натуральным логарифмом и обозначается ln(x).

б) 0 < а < 1

1. log ax определена для 0<x<+. 2. log ax строго монотонно убывает. 3. log ax непрерывна. 4.  .

Основное свойство логарифмической функции имеет вид:

.

Докажем это свойство. Действительно, используя тот факт, что логарифмическая функция является функцией, обратной показательной, мы можем записать

, .

Но тогда, используя основное свойство показательной функции, получаем

.

Снова используя тот факт, что логарифмическая функция является функцией, обратной показательной, получаем

,

что и требовалось доказать.

Можно показать, что log_ax – единственная непрерывная функция, удовлетворяющая свойству .

Другие важные формулы, касающиеся логарифмической функции

а) ;

б) .

Степенная функция

Функция где  – произвольное вещественное число, называется степенной функцией. В общем случае она определяется следующим образом:

.

Из этого определения следуют и все ее свойства.

1. Так как функция определена для , то и степенная функция в общем случае определена лишь для (хотя для случая, когда   целое число, ее определяют и для отрицательных значений х).

2.   непрерывная функция, как суперпозиция непрерывных функций.

3. Монотонность.

Имеем для :

,

то есть при степенная функция является строго монотонно возрастающей функцией.

Аналогично, для ,

,

то есть при степенная функция является строго монотонно убывающей функцией.

4. Поведение при и при .

Имеем для :

,

.

Аналогично, для ,

,

.

Тригонометрические функции

Так как эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Рассмотрим лишь вопрос об их непрерывности. Основным здесь для нас будет неравенство , которое мы примем без доказательства.

Функция sin x .

Имеем

,

так что sin x₀ непрерывен при любом х₀.

Функция cos x.

Аналогично предыдущему, имеем

,

так что cos x₀ непрерывен при любом х₀.

Функция tg x.

Так как функции sin(x) и cos(x) непрерывны для всех x, то имеет разрывы второго рода в точках, где cos(x)=0, то есть в точках При остальных значениях аргумента tg(x) непрерывен.

Обратные тригонометрические функции

arc sin(x)

Рассмотрим график функции у=sin(x) и на этом графике рассмотрим лишь участок .

Функция, обратная к sin(x) только на этом участке, называется главной ветвью arcsin x. Именно ее мы и будем изучать.

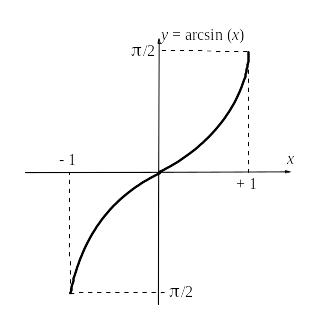
1. Так как –1  sin x  +1, то arcsin x определен для –1  x  +1.

2. Так как на выделенном участке sin x строго монотонно возрастает, то arcsin x тоже строго монотонно возрастает.

3. Так как sin x непрерывна, то и arcsin x тоже непрерывна.

4.  .

5. 

arc cos(x)

Выделим на графике функции у=cos (x) участок 0  x  . Функцию, обратную к cos x именно на этом участке, будем называть главной ветвью arc cos x и именно ее будем изучать и использовать.

1. Так как –1  cos x  +1, то arccos x определен для –1  x  +1.

2. Так как на выделенном участке cos x строго монотонно убывает, то arccos x тоже строго монотонно убывает.

3. Так как на выделенном участке cos x непрерывна, то arccos x тоже непрерывна.

4. .

arc tg(x)

На графике функции у=tg(x) выделим лишь участок . Функцию, обратную к tg x именно на этом участке будем называть главной ветвью arctg x.

1. arctg x определен для – < x < +.

2. Так как на выделенном участке tg x строго монотонно возрастает, то arctg x тоже строго монотонно возрастает.

3. Так как на выделенном участке tg x непрерывна, то и arctg x тоже непрерывна.

4. arctg(x)=-arctg(x)

5.  .