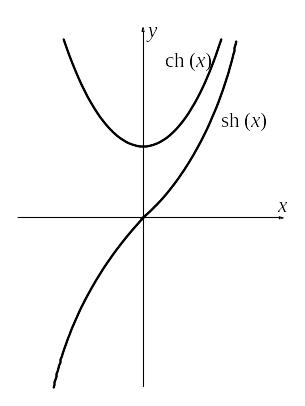3.8 Непрерывность элементарных функций.
Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся:
а)
показательная функция
;
б) гиперболические функции sh(x), ch(x), th(x);
в) логарифмическая функция у=loga(x);
а)
степенная функция
;
д) тригонометрические функции sin(x), cos(x), tg(x);
е) обратные тригонометрические функции arc sin(x), arc cos(x), arc tg(x).
Все возможные суперпозиции этих функций также называются элементарными.
Далее мы сделаем небольшой обзор свойств этих функций, особо обращая внимание на их непрерывность.
Показательная функция.
.
Мы не будем давать строгого определения показательной функции, так как изложенного выше материала для этого недостаточно. Будут изучены лишь свойства этой функции.
Рассмотрим
подробно случай
1. Основное свойство показательной функции имеет вид
.
Иногда
именно это свойство принимается в
качестве определения показательной
функции, так как можно показать, что
среди непрерывных функций показательная
функция – единственная функция,
удовлетворяющая свойству
.
Следствием этого свойства является
следующее свойство показательной
функции:
.
2. Если
,
то
;
при любых значениях х
.
3. При
функция
строго монотонно возрастает.
Пусть
.
Тогда
и мы имеем
,
так
как
>1.
Следовательно
.
4. 
.
Представим а в виде а =1 + . Тогда >0.
Пусть х = n где n целое положительное число. Тогда, используя формулу бинома Ньютона, получим
.
Следовательно
.
Пусть
теперь х > 0
и n = [x]
есть целая часть х.
Тогда
;
при х+
также и n+
и мы имеем
.
5. 
.
Действительно,
.
При
,
и
6 .
непрерывна при любом х.
Пусть
.
Возьмем любое
и найдем такое целое число n,
чтобы выполнялось соотношение
.
Можно ли это сделать?
Имеем следующую цепочку неравенств.
;
;
;
;
.
Поэтому, если мы добьемся выполнения неравенства
,
то предыдущее неравенство будет и подавно выполнено. Но последнее неравенство верно при
,
так что искомое n всегда существует.
Но тогда, при х, удовлетворяющем неравенству
имеем
,
и функция ax непрерывна в точке х0 справа.
Аналогично доказывается, что функция ax непрерывна в точке х0 слева, и поэтому функция ax непрерывна в точке х0.
7. Значения функции ax заполняют сплошь отрезок (0, +).
Случай
0 < a < 1
рассматривается аналогично. В этом
случае функция ax
строго монотонно убывает, непрерывна
при любых х,
и
.
Ее значения также заполняют сплошь
отрезок (0, +).
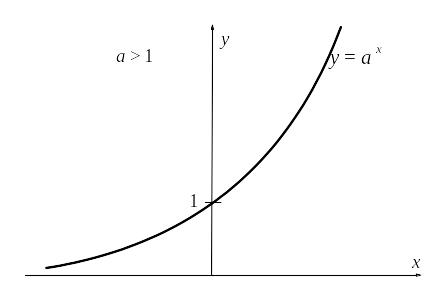
Вид графика показательной функции при а > 1 и при 0 < a < 1 приведен на рисунке.
|
|
Математики
особенно «любят» функцию
,
то есть показательную функцию при а=е.
Ее называют экспоненциальной функцией,
или просто экспонентой. Для нее часто
используют обозначение
.
Гиперболические функции.
С функцией ex тесно связаны функции, получившие название гиперболических. К ним относятся:
гиперболический
синус 
гиперболический
косинус 
гиперболический
тангенс 
Рассмотрим коротко свойства этих функций.
|
|
1. Область определения этих функций <x<+
2. sh(x)= –sh(x), th(x)= –th(x), ch(x)= ch(x), то есть sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках.
3. sh(х), ch(x) и th(x) непрерывны для всех х.
4. sh(x) и th(x) монотонно возрастают.
5. Выведем основные формулы, касающиеся этих функций, и очень напоминающие формулы тригонометрии.
а) ch2(x) sh2(x)=1.
Действительно,
б)
Вывод этой формулы надо вести с правой части. Имеем:
в)
.
Аналогично имеем:
Аналогично
выводятся формулы и для комбинации
.
Можно вывести и много других формул,
аналогичных формулам геометрии.