3.6 Монотонные функции.
Докажем теперь две теоремы, касающиеся непрерывности монотонных функций.
Теорема 1. Пусть f(x) определена и монотонна на замкнутом отрезке [a, b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки).
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
|
Возьмем
какую-то точку x0[a,
b].
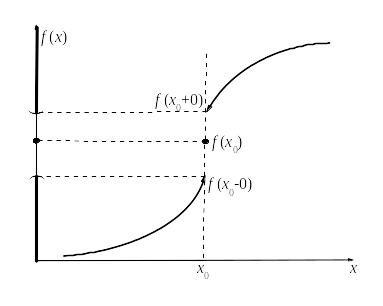
Пусть мы приближаемся к точке х0
слева
(см. рис.). Тогда при этом значения
функции f(x)
будут монотонно возрастать.
Но они будут ограничены сверху,
например, величиной f(x0).
Поэтому, по теореме о пределе монотонно
возрастающей функции будет существовать
конечный
При
движении к х0
справа
значения f(x)
будут монотонно убывать,
но будут ограничены снизу
величиной f(x0).
Поэтому снова существует конечный
|
.
.Если f(x0+0) = f(x00), то f(x) будет непрерывна в точке х0, если же f(x0+0)>f(x00), то у f(x) в точке х0 будет разрыв I рода.
Определение. Говорят, что значения функции f(x), определенной на <a, b>, заполняют некоторый отрезок <c, d> сплошь, если
.
Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a, b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь.
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
1. Достаточность.
Пусть f(x)
непрерывна на [a, b].
Тогда
,
.
Согласно второй теореме Больцано-Коши,
.
Поэтому отрезок [f(a), f(b)] заполнен сплошь.
2. Необходимость. При доказательстве необходимости в этой теореме используется достаточно редко применяемый прием. Он основан на следующем соотношении из алгебры логики
.
Вместо
того, чтобы доказывать, что
доказывают, что
.
В нашем случае это выглядит так: вместо того, чтобы доказывать следование «функция заполняет некоторый отрезок сплошь она непрерывна», доказывают следование «функция не непрерывна ее значения не заполняют отрезок сплошь».
Итак: пусть f(x) не является непрерывной на [a, b]. Тогда она на [a, b] может иметь только разрывы I рода. Пусть х0 – координата такого разрыва. Возможные варианты поведения графика f(x) изображены на рисунках.
|
|
Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь.
3.7 Обратная функция. Теорема о существовании обратной функции у монотонной функции.
Определение. Пусть имеется функция f(x) определенная на отрезке <a, b>, значения которой принадлежат некоторому отрезку <c, d>. Если
,
то
говорят, что на отрезке <c,
d>
определена функция, обратная
к функции
f(x)
и обозначают это так:
.
Обратите
внимание на отличие этого определения
от определения заполненности отрезка
<c, d>
сплошь. В определении
стоит квантор
,
то есть значение х,
обеспечивающее равенство
,
должно быть единственным,
в то время как в определении заполненности
отрезка<c, d>
сплошь стоит квантор
,
что говорит о том, что может быть несколько
значений х,
удовлетворяющих равенству
.
Обычно,
говоря об обратной функции, заменяют х
на у
а y
на x
(xy)
и пишут
.
Очевидно, что исходная функция f(x)
и обратная функция
удовлетворяют соотношению
.
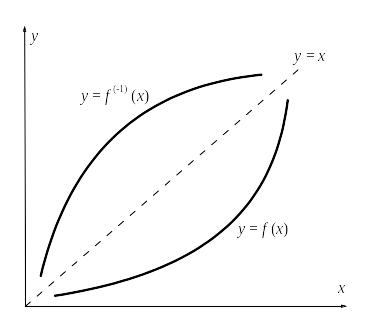
Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.
Пример.
Пусть
,
Чтобы найти обратную функцию, надо
проделать следующие операции:
1.
Уравнение
разрешить относительно y:
.
2. В
получившемся выражении сделать замену
:
.
Таким образом
.
Теорема. Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a, b]. Тогда на отрезке [f(a), f(b)] определена обратная функция , которая также непрерывна и строго монотонно возрастает (убывает).
Доказательство.
Докажем теорему для случая, когда f(x) строго монотонно возрастает.
1. Существование обратной функции.
Так
как по условию теоремы f(x)
непрерывна, то, согласно предыдущей
теореме, отрезок [f(a), f(b)]
заполнен сплошь. Это означает, что
.
Докажем,
что х
единственно. Действительно, если взять
,
то будет
и поэтому
.
Если взять
,
то будет
и поэтому
.
В обоих случаях значения функции не
равны y,
и поэтому x
единственно. Следовательно,
и
существует.
2. Монотонность обратной функции.
Сделаем
обычную замену xy
и будем писать
.
Это значит, что
.
Пусть x1 > x2. Тогда:
; 
;
; 
.
Какое же соотношение между y1 и y2? Проверим возможные варианты.
а) y1 < y2? Но тогда f(y1)<f(y2) и x1 < x2, а у нас было x1>x2.
б) y1 = y2? Но тогда f(y1)=f(y2) и x1=x2, а у нас было x1>x2.
в)
Остается единственный вариант y1>y2.
Но тогда
,
а это и означает, что
строго монотонно
возрастает.
3. Непрерывность обратной функции.
Так как значения обратной функции заполняют сплошь отрезок [a, b], то по предыдущей теореме, непрерывна.