Розділ 1. Основи штучних нейрони мереж

1.1. Біологічний прототип штучного нейрона – біологічний нейрон. Модель штучного нейрона. Активаційна функція.

Біологічний прототип штучного нейрона-біологічний нейрон.

Інтелектуальна діяльність людини базується на функціонуванні величезної кількості (≈10⁵⁰) особливих клітин-нейронів.При цьому важливим ж їх взаємодія і передача сигналів між ними. У людському мозку між нейронами протягом життя встановлюється (≈ 10¹⁴⁾різних зв’язків по яких передаються сигнали.Комбінування таких сигналів формує інтелект людини.В процесі життя, розвитку,навчання можуть встановлюватися нові зв’язкі,окремі посилюватись інші послаблюватись.Це все формує дослід людини.

Особливостями інтелекту функціонування нервових клітин активно займалися з кінця ХIX і початку ХХ ст. Фізіологи встановили що більшість нервових клітин функціонують подібно між собою і були встановлені основні аспекти їх функціонування.З середини ХХ ст. до цих досліджень долучилися математики які запропонували ряд математичних моделей,що описували функціонування нейронів та взаємодію між ними.З’ясувалося, що математичні моделі дозволяли вирішувати ряд задач по класифікації образу,ідентифікації прогнозування поведінки тощо.Це дозволило застосувати такі моделі для вирішення тих задач, які традиційними методами алгоритмічного моделювання невирішувались.

Прототипом математичної моделі штучного нейрона був біологічний нейрон.Не зважаючи на усю складність будови і функціонування в біологічному нейроні можна виділити 5 наступних основних елементів

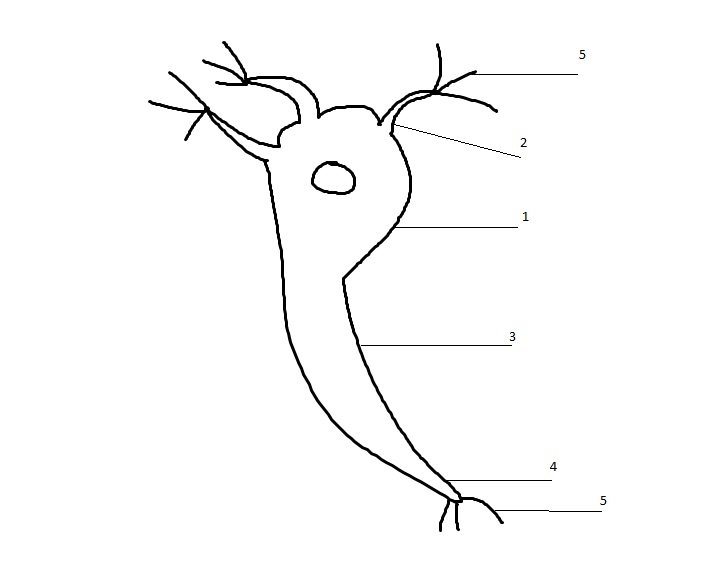
1-тіло нейрона або сома;

2-сукупність відростків – дендритів, по яких переважно передаються вхідні сигнали

3- особливе потовщення на тілі нейрона, що називається аксонним горбком, тут формується вихідний сигнал

4- в преважній більшості 1 довгий відросток (аксон) по аксону переважно передаються вихідні сигнали

5- особливі розгалуження відростків через які здійснюються з’єднання нейронів – синапси, зв’язкі нейронів через сигнали називаються синаптичними.

Нейрони можуть з’єднуватися як між собою, так і з м’язовими чи іншими тканинами, до яких поступає остаточний сигнал.Функціонування такої спрощеної моделі можна описати так :

-Через синаптичні зв’язкі по дендритах до соми надходить сукупність сигналів різної сили, величина кожного із сигналів може змінюватися(посилюватися чи послаблюватися) в залежності від особливості відповіді дендритів

-У сомі виконується сумування усіх сигналів із врахуванням їх посилення чи послаблення

-Сумарний вхідний сигнал співставляються із так званими пороговим значенням активації нейрона: якщо відбувається перевищення порогу то у аксонному горбку генерації виходить сигнал певної величини – нейрон збуджений тобто переходить в активний стан;якщо перевищення пороку активації немає, то нейрон залишається в пасивному стані – виходить сигнал не генерований або він є слабкий

-Згенерований вихідний сигнал по аксону через вихідний синапсис передається далі

Якщо розглядати складну систему пов’язаних між собою нейронів яка має деяку множину вхідних каналів і деяку вихідних то таку сукупність можна вважати особливим перетворювачем деякої множини n-вхідних сигналів, у деяку множину m-вихідних сигналів.

Побудова математичних моделей нейронних систем передбачає розробку таких алгоритмів які б забезпечили функіонування цих перетворювачів аналогічно до людскої інтелектуальної діяльності.При цьому процес налаштування такого перетворювача нагадує процес навчання нейронних систем.Навчання має на меті формувати такі вихідні сигнали для відповідного вхідного набору,які відповідатимумть потребам людини(аналогія з формуванням умовного рефлексу).

Процес навчання спрощено можна описати так:

-якщо для деякого вхідного набору сигналів на виході має бути активний сигнал, і дійсно нейрон активується, то реакція нейрона вважається адекватною і корекції його функіонування немає потреби;

-ящо для деякого вхідного набору сигналу на виході немає бути вихідного сигналу(пасивний)

Але насправді нейрон активується, то реакція невірна, при цьому потрібно зменшити його активність, це може бути досягнуто або шляхом послаблення вхідних каналів, або збільшити поріг активації

-якщо для вхідного набору сигналів немає бути сигналу, тобто нейрон пасивний і він дійсно залишається пасивним,то реакція лишається адекватною і корекція його функціонування непотрібна

-якщо для деякого вхідного набору сигналів на виході має бути активний сигнал тобто нейрон активується,але насправді нейрон залишається пасивним,то реакція нейрона невірна при цьому потрібно збільшити активність нейрона,це може бути досягнуто або шляхом посилення вхідних каналів, або шляхом пониження порогу активації

Процес навчання нейрона не є однокроковим.Перевірка активності повинна виконуватися для всеможливих випадків вхідних даних і продовжуватися до тих пір поки реакція нейрона в кожному випадку нестане адекватною.Якщо таке має місце то говорять що нейрон навчений на даній навчальній множині.

Модель штучного нейрона

Штучний нейрон (ШН) – це математична модель функціонування біологічного нейрона, у ньому так само можна виділити основні елементи, ці елементи матимуть математичний зміст, але їх функціонування моделюватиме функціонування біологічних компонентів

В якості дендритів у ШН, використовуютьсятак звані вхідні канали із своїми ваговими коефіцієнтами посилення чи послаблення сигналу.

W_i,

На кожен із входів подається відповідний сигнал Х_і, 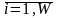. Таким чином можна говорити про вектор вхідних сигналів і про вектор вагових коефіцієнтів входів

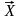=(X₁,X₂,…,X_n)

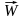=(W₁,W₂,…,W_n)

Процес сумування усіх вхідних сигналів з врахуванням їх посилення чи послаблення моделюється функцією скалярного добутку

Ʃ=X₁W₁+X₂W₂+…+X_nW_n=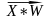 (1)

Співставлення сумарного зваженого сигналу з порогу активації нейрона та генерування вихідного сигналу можна моделювати деякою функцією

Out=F(Ʃ) (2)

Вибір функції f може бути достатньо довільний і залежить від дослідження моделі.Таким чином схематично модель ШН можна зобразити так:

x ₁w₁

x₂w₂ Z= · 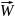F(Ʃ) Out

. . . . . . .

x_nw_n

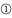② ③ ④ ⑤

Тут : ① – вектор вхідних сигналів

② – вектор вагових коефіцієнтів

③ – суматор що реалізує складніший добуток

④ – передатна функція( функція активації) ШН що визначає величину вихідного сигналу ⑤

⑤ – вихідний сигнал

Вибір передатної функції залежить від моделі функціонування ШН,у найпростішому випадку стрибкоподібної активності нейрона при досягнені деякого порогу активності Р, функція до активації є пороговою функцією стрибка

1 _

P

F(∑)=

Вибір порогу активації ШН, може бути достатньо довільним очевидно якщо Р є малим то ШН легко збуджується якщо ж Р велике то ШН активізується значно важче або при великих вхідних сигналах х_і, або при великих значеннях вагових коефіцієнтів вхідних каналів W_i

Вибір передатної функції. Передатна функція визначає величину вихідного сигналу штучного нейрона розглянутий вище приклад порогової функції стрибка є найбільш спрощеною моделлю.

У реальних біопроцесах передача сигналів по нейронах не є миттєвою і стрибкоподібної насправді відбувся процес насичення або пологе або стрімке зростання після якого знову може бути зона до насичення.

Такій процес може бути змодельований належним вибором передатної функції можливі наступні випадки

a) out

P₁ P₂ Ʃ

Це є модель із лінійною передатною функцією баз насичення із діапазонною активністю від Р₁ до Р₂

б)

o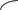 ut_{2 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _}

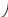o ut₁ _ _ _ _ _ _ _

P Ʃ

Модель порогової функції з насиченням із точкою активації Р, при цьому вихідних сигнал полого зростає при насиченні ШН до порогового значення Р.Далі у точці насичення Р вих. Сигнал зростає без збільшення величини суматора до деякої величини out₁.

Далі величина вихідного сигналу полого зростає до деякої граничної величини out₂із збільшенням значення сумматора.

в)

out

o ut_{1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _}

P Ʃ

Це модель передатної функції або із так званою сигмоєдною або логістичною функцією.Дана модель найкраще відповідає реальним біологічним процесам у нейронах.Така функція реалізує неперервне відображення величини суматорів на деякий інтервал значень вихідних сигналів.

Якщо ШН моделює явище чи процес у якому вхідні чи вихідні сигнали можуть бути з довільним діапазоном значень [a;b], то передатна функція може будуватися на основі розгляданих вище схем із зміщенням по осі абсцис або по осі координат

b _{_ _ _ _ _ _ _}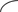

_{_ _ _}

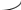a

P Ʃ

Часто в якості передатної функції використовується сигмоїдна логістична функція виду

F(Ʃ)=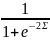 (1)

Cхематичний графік цієї функції наступний

F(Ʃ)

1_ _ __

Ʃ

Якщо вихід ШН має бути із симетричного інтервалу [-b;b] то сигмоїд виду (1) можна перетворити так

(Ʃ)=2b(F(Ʃ)- )=2b(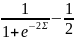 )