Лекция 1. Основные понятия и термины мед статистики 03.09.12

Лекция 2. Рандомизация и мета анализ 10.09.12

Лекция 3. Основные типы планов 17.09.12

Лекция 4. Анализ выживаемости 24.09.12

Лекция 1. Основные понятия и термины мед статистики 03.09.12

Вариация

Определение. Степень рассеяния данных (значений признака) по области значений

Вероятность

Определение. Вероятность(probability) – степень возможности проявления какого – либо определённого события в тех или иных условиях.

Пример. Поясним определение термина на предложении «Вероятность выздоровления при применении лекарственного препарата Aримидекс равна 70%». Событием является «выздоровление больного», условием «больной принимает Аримидекс», степенью возможности – 70% (грубо говоря, из 100 человек, принимающих Аримидекс, выздоравливают 70).

Кумулятивная вероятность

Определение. Кумулятивная вероятность выживания (Cumulative Probability of surviving) в момент времени t – это то же самое, что доля выживших пациентов к этому моменту времени.

Пример. Если говорится, что кумулятивная вероятность выживания после проведения пятилетнего курса лечения равна 0.7, то это значит, что из рассматриваемой группы пациентов в живых осталось 70% от начального количества, а 30% умерло. Другими словами, из каждой сотни человек 30 умерло в течение первых 5 лет.

Время до события

Определение. Время до события – это время, выраженное в некоторых единицах, прошедшее с некоторого начального момента времени до наступления некоторого события.

Пояснение. В качестве единиц времени в медицинских исследованиях выступают дни, месяцы и годы.

Типичные примеры начальных моментов времени:

• начало наблюдения за пациентом

• проведение хирургического лечения

Типичные примеры рассматриваемых событий:

• прогрессирование болезни

• возникновение рецидива

• смерть пациента

Выборка

Определение. Часть популяции, полученная путем отбора.

По результатам анализа выборки делают выводы о всей популяции, что правомерно только в случае, если отбор был случайным. Поскольку случайный отбор из популяции осуществить практически невозможно, следует стремиться к тому, чтобы выборка была по крайней мере репрезентативна по отношению к популяции.

Зависимые и независимые выборки

Определение. Выборки, в которые объекты исследования набирались независимо друг от друга. Альтернатива независимым выборкам – зависимые (связные, парные) выборки.

Гипотеза.

Двусторонняя и односторонняя гипотезы

Сначала поясним применение термина гипотеза в статистике.

Цель большинства исследований - проверка истинности некоторого утверждения. Целью тестирования лекарственных препараторов чаще всего является проверка гипотезы, что одно лекарство эффективнее другого (например, Аримидекс эффективнее Тамоксифена).

Для предания строгости исследования, проверяемое утверждение выражают математически. Например, если А – это количество лет, которое проживёт пациент, принимающий Аримидекс, а Т –это количество лет, которое проживёт пациент, принимающий Тамоксифен, то проверяемую гипотезу можно записать как А>Т.

Определение. Гипотеза называется двусторонней (2-sided), если она состоит в равенстве двух величин.

Пример двусторонней гипотезы: A=T.

Определение. Гипотеза называется односторонней (1-sided),если она состоит в неравенстве двух величин.

Примеры односторонних гипотез:

• 

• 

• 

• 

Дихотомические (бинарные) данные 

Определение.  Данные, выражаемые только двумя допустимыми альтернативными значениями

Пример: Пациент «здоров» - «болен». Отек "есть" - "нет".

Дихотомические (бинарные) данные 

Определение.  Данные, выражаемые только двумя допустимыми альтернативными значениями Пример: Пациент «здоров» - «болен». Отек "есть" - "нет".

Доверительный интервал

Определение. Доверительный интервал (confidence interval) для некоторой величины - это диапазон вокруг значения величины, в котором находится истинное значение этой величины (с определенным уровнем доверия).

Пример. Пусть исследуемой величиной является количество пациентов в год. В среднем их количество равно 500, а 95% -доверительный интервал – (350, 900). Это означает, что, скорее всего (с вероятностью 95%), в течение года в клинику обратятся не менее 350 и не более 900 человек.

Обозначение. Очень часто используются сокращение: ДИ 95 % (CI 95%) – это доверительный интервал с уровнем доверия 95%.

Достоверность, статистическая значимость (P – уровень)

Определение. Статистическая значимость результата – это мера уверенности в его "истинности".

Любое исследование проходит на основе лишь части объектов. Исследование эффективности лекарственного препарата проводится на основе не вообще всех больных на планете, а лишь некоторой группы пациентов (провести анализ на основе всех больных просто невозможно).

Предположим, что в результате анализа был сделан некоторый вывод (например, использование в качестве адекватной терапии препарата Аримидекс в 2 раза эффективнее, чем препарата Тамоксифен).

Вопрос, который необходимо при этом задавать: "Насколько можно доверять этому результату?".

Представьте, что мы проводили исследование на основе только двух пациентов. Конечно же, в этом случае к результатам нужно относиться с опасением. Если же были обследовано большое количество больных (численное значение «большого количества» зависит от ситуации), то сделанным выводам уже можно доверять.

Так вот, степень доверия и определяется значением p-уровня (p-value).

Более высокий p- уровень соответствует более низкому уровню доверия к результатам, полученным при анализе выборки. Например, p- уровень, равный 0.05 (5%) показывает, что сделанный при анализе некоторой группы вывод является лишь случайной особенностью этих объектов с вероятностью только 5%.

Другими словами, с очень большой вероятностью (95%) вывод можно распространить на все объекты.

Во многих исследованиях 5% рассматривается как приемлемое значение p-уровня. Это значит, что если, например, p= 0.01, то результатам доверять можно, а если p=0.06, то нельзя.

Исследование

Проспективное исследование – это исследование, в котором выборки выделяются на основе исходного фактора, а в выборках анализируется некоторый результирующий фактор.

Ретроспективное исследование – это исследование, в котором выборки выделяются на основе результирующего фактора, а в выборках анализируется некоторый исходный фактор.

Пример. Исходный фактор – беременная женщина моложе/старше 20 лет. Результирующий фактор - ребёнок легче/тяжелее 2,5 кг . Анализируем, зависит ли вес ребёнка от возраста матери.

Если мы набираем 2 выборки, в одной – матери моложе 20 лет, в другой – старше, а затем анализируем массу детей в каждой группе, то это проспективное исследование.

Если мы набираем 2 выборки, в одной – матери, родившие детей легче 2,5 кг, в другой – тяжелее, а затем анализируем возраст матерей в каждой группе, то это ретроспективное исследование (естественно, такое исследование можно провести, только когда опыт закончен, т.е. все дети родились).

Исход

Определение. Клинически значимое явление, лабораторный показатель или признак, который служит объектом интереса исследователя. При проведении клинических испытаний исходы служат критериями оценки эффективности лечебного или профилактического воздействия.

Клиническая эпидемиология

Определение. Наука, позволяющая осуществлять прогнозирование того или иного исхода для каждого конкретного больного на основании изучения клинического течения болезни в аналогичных случаях с использованием строгих научных методов изучения больных для обеспечения точности прогнозов.

Когорта

Определение. Группа участников исследования, объединенных каким-либо общим признаком в момент ее формирования и исследуемых на протяжении длительного периода времени.

Контроль

Контроль исторический

Определение.  Контрольная группа, сформированная и обследованная в период, предшествующий исследованию.

Контроль параллельный

Определение. Контрольная группа, формируемая одновременно с формированием основной группы.

Корреляция

Определение. Статистическая связь двух признаков (количественных или порядковых), показывающая, что большему значению одного признака в определенной части случаев соответствует большее – в случае положительной (прямой) корреляции – значение другого признака или меньшее значение – в случае отрицательной (обратной) корреляции.

Пример. Между уровнем тромбоцитов и лейкоцитов в крови пациента обнаружена значимая корреляция. Коэффициент корреляции равен 0,76

Коэффициент риска (КР) Определение. Коэффициент риска (hazard ratio) – это отношение вероятности наступления некоторого («нехорошего») события для первой группы объектов к вероятности наступления этого же события для второй группы объектов.

Пример. Если вероятность появления рака лёгких у некурящих равна 20%, а у курильщиков – 100%, то КР будет равен одной пятой. В этом примере первой группой объектов являются некурящие люди, второй группой – курящие, а в качестве «нехорошего» события рассматривается возникновение рака лёгких.

Интерпретация значения величины. Очевидно, что:

1) если КР=1, то вероятность наступления события в группах одинаковая

2) если КР>1, то событие чаще происходит с объектами из первой группы, чем из второй

3) если КР<1, то событие чаще происходит с объектами из второй группы, чем из первой

Мета-анализ

Определение. Статистический анализ, обобщающий результаты нескольких исследований, исследующих одну и ту же проблему (обычно эффективность методов лечения, профилактики, диагностики). Объединение исследований обеспечивает большую выборку для анализа и большую статистическую мощность объединяемых исследований. Используется для повышения доказательности или уверенности в заключении об эффективности исследуемого метода.

Метод Каплана – Мейера (Множительные оценки Каплана – Мейера)

Этот метод был придуман статистиками Е.Л.Капланом и Полем Мейером.

Метод используется для вычисления различных величин, связанных с временем наблюдения за пациентом. Примеры таких величин:

• вероятность выздоровления в течении одного года при применении лекарственного препарата

• шанс возникновения рецидива после операции в течении трёх лет после операции

• кумулятивная вероятность выживания в течение пяти лет среди пациентов с раком простаты при ампутации органа

Поясним преимущества использования метода Каплана - Мейера.

Значение величин при «обычном» анализе (не использующем метод Каплана-Мейера) рассчитываются на основе разбиения рассматриваемого временного интервала на промежутки.

Например, если мы исследуем вероятность смерти пациента в течение 5 лет, то временной интервал может быть разделён как на 5 частей (менее 1 года, 1-2 года, 2-3 года, 3-4 года, 4-5 лет), так и на 10 (по полгода каждый), или на другое количество интервалов. Результаты же при разных разбиениях получатся разные.

Выбор наиболее подходящего разбиения – непростая задача.

Оценки значений величин, полученных по методу Каплана- Мейера не зависят от разбиения времени наблюдения на интервалы, а зависят только от времени жизни каждого отдельного пациента.

Поэтому исследователю проще проводить анализ, да и результаты нередко оказываются качественней результатов «обычного» анализа.

Кривая Каплана –Мейера (Kaplan – Meier curve)– это график кривой выживаемости, полученной по методу Каплана-Мейера.

Модель Кокса

Эта модель была придумана сэром Дэвидом Роксби Коксом (р.1924), известным английским статистиком, автором более 300 статей и книг.

Модель Кокса используется в ситуациях, когда исследуемые при анализе выживаемости величины зависят от функций времени. Например, вероятность возникновения рецидива через t лет (t=1,2,…), может зависеть от логарифма времени log(t).

Важным достоинством метода, предложенного Коксом, является применимость этого метода в большом количестве ситуаций (модель не накладывает жестких ограничений на природу или форму распределения вероятностей).

На основе модели Кокса можно проводить анализ (называемый анализом Кокса (Cox analysis)), результатом проведения которого является значение коэффициента риска и доверительного интервала для коэффициента риска.

Непараметрические методы статистики

Определение. Класс статистических методов, которые используются главным образом для анализа количественных данных, не образующих нормальное распределение, а также для анализа качественных данных.

Пример. Для выявления значимости различий систолического давления пациентов в зависимости от типа лечения воспользуемся непараметрическим критерием Манна-Уитни.

Признак (переменная)

Определение. Характеристика объекта исследования (наблюдения). Различают качественные и количественные признаки.

Рандомизация

Определение. Способ случайного распределения объектов исследования в основную и контрольную группы с использованием специальных средств (таблиц или счетчика случайных чисел, подбрасывания монеты и других способов случайного назначения номера группы включаемому наблюдению). С помощью рандомизации сводятся к минимуму различия между группами по известным и неизвестным признакам, потенциально влияющим на изучаемый исход.

Риск

Атрибутивный – дополнительный риск возникновения неблагоприятного исхода (например, заболевания) в связи с наличием определенной характеристики (фактора риска) у объекта исследования. Это часть риска развития болезни, которая связана с данным фактором риска, объясняется им и может быть устранена, если этот фактор риска устранить.

Относительный риск – отношение риска возникновения неблагоприятного состояния в одной группе к риску этого состояния в другой группе. Используется в проспективных и наблюдательных исследованиях, когда группы формируются заранее, а возникновение исследуемого состояния ещё не произошло.

Скользящий экзамен

Определение. Метод проверки устойчивости, надежности, работоспособности (валидности) статистической модели путем поочередного удаления наблюдений и пересчета модели. Чем более сходны полученные модели, тем более устойчива, надежна модель.

Событие

Определение. Клинический исход, наблюдаемый в исследовании, например возникновение осложнения, рецидива, наступление выздоровления, смерти.

Стратификация

Определение. Метод формирования выборки, при котором совокупность всех участников, соответствующих критериям включения в исследование, сначала разделяется на группы (страты) на основе одной или нескольких характеристик (обычно пола, возраста), потенциально влияющих на изучаемый исход, а затем из каждой из этих групп (страт) независимо проводится набор участников в экспериментальную и контрольную группы. Это позволяет исследователю соблюдать баланс важных характеристик между экспериментальной и контрольной группами.

Таблица сопряженности

Определение. Таблица абсолютных частот (количества) наблюдений, столбцы которой соответствуют значениям одного признака, а строки – значениям другого признака (в случае двумерной таблицы сопряженности). Значения абсолютных частот располагаются в клетках на пересечении рядов и колонок.

Приведем пример таблицы сопряженности. Операция на аневризме была сделана 194 пациентам. Известен показатель выраженности отека у пациентов перед операцией.

Отек\ Исход	Выжил	Умер	ni
нет отека	20	6	26
умеренный отек	27	15	42
выраженный отек	8	21	29
mj	55	42	194

Таким образом, из 26 пациентов, не имеющих отека, после операции выжило 20 пациентов, умерло - 6 пациентов. Из 42 пациентов, имеющих умеренный отек выжило 27 пациентов, умерло - 15 и т.д.

Критерий хи-квадрат для таблиц сопряженности

Для определения значимости (достоверности) различий одного признака в зависимости от другого (например, исхода операции в зависимости от выраженности отека) применяется критерий хи-квадрат для таблиц сопряженности:

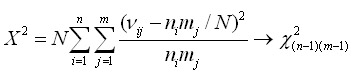
Шанс

Пусть вероятность некоторого события равна p. Тогда вероятность того, что событие не произойдёт равна 1-p.

Например, если вероятность того, что больной останется жив спустя пять лет равна 0.8 (80%), то вероятность того, что он за этот временной промежуток умрёт равна 0.2 (20%).

Определение. Шанс – это отношение вероятности того, что события произойдёт к вероятности того, что событие не произойдёт.

Пример. В нашем примере (про больного) шанс равен 4, так как 0.8/0.2=4

Таким образом, вероятность выздоровления в 4 раза больше вероятности смерти.

Интерпретация значения величины.

1) Если Шанс=1, то вероятность наступления события равна вероятности того, что событие не произойдёт;

2) если Шанс >1, то вероятность наступления события больше вероятности того, что событие не произойдёт;

3) если Шанс <1, то вероятность наступления события меньше вероятности того, что событие не произойдёт.

Отношение шансов

Определение. Отношение шансов (odds ratio) – это отношение шансов для первой группы объектов к отношению шансов для второй группы объектов.

Пример. Допустим, что некоторое лечение проходят и мужчины, и женщины.

Вероятность того, что больной мужского пола останется жив спустя пять лет равна 0.6 (60%); вероятность того, что он за этот временной промежуток умрёт равна 0.4 (40%).

Аналогичные вероятности для женщин равны 0.8 и 0.2.

Отношение шансов в этом примере равно

Интерпретация значения величины.

1) Если отношение шансов =1, то шанс для первой группы равен шансу для второй группы

2) Если отношение шансов >1, то шанс для первой группы больше шанса для второй группы

3) Если отношение шансов <1, то шанс для первой группы меньше шанса для второй группы

Типы графиков, наиболее часто

используемые при визуальном анализе

■ Гистограмма (Frequency plot, Histogram, Bar chart)

■ График средних с ошибками (Error bar plot)

■ Диаграмма размаха (Box&whisker plot)

■ Диаграмма рассеяния (Scatter plot)

■ Диаграмма концентрации (Bag plot)

■ Диаграмма Вороного (Voronoi diagram)

■ Лица Чернова (Chernoff faces)

■ Категоризованные графики (Categorized plots) Основное назначение: визуализация данных, разбитых на группы, для более точного и детального анализа Гистограмма –столбчатая диаграмма распределения частот для выбранной переменной.

Применение лиц Чернова

выявление характерных зависимостей или

групп наблюдений

наглядная визуализация результатов

исследование предположительно сложных

взаимосвязей между несколькими переменными

заголовок графика должен быть кратким,

информативным и недвусмысленным

■ на осях, сегментах и решетках должны быть

пометки; объясняйте значение символов

■ постарайтесь уместить на графике всю нужную

информацию

■ делайте график простым, отказывайтесь от

ненужных украшений (например, для диаграммы не

обязательно делать столбцы трехмерными)

Лекция 2. Рандомизация и мета анализ 10.09.12

Исходные данные

Имеются данные о пациентах, поступивших в больницу для трансплантации сердца. Таблица с данными имеет вид:

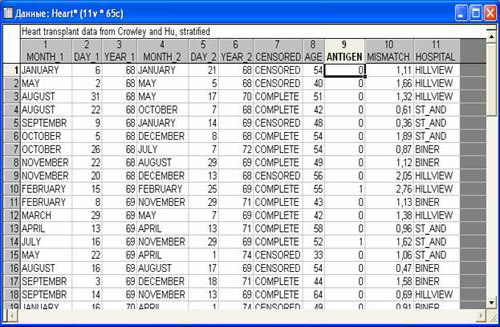
Рис 1. Исходный файл данных

Первые три столбца в этой таблице есть даты трансплантации сердца (в следующей последовательности: месяц-день-год), 4, 5 и 6 столбцы - даты, когда соответствующий пациент либо умер, либо был изъят из наблюдения (иными словами, цензурирован, например, с пациентом была утрачена связь).

Переменная Цензурировано - Censored является индикатором цензурирования с кодом, который показывает, является соответствующее наблюдение завершенным или цензурированным (0-завершенно, т.е. пациент умер; 1-цензурированное). Переменная Age – возраст пациента, Antigen – показатель несовместимости антигенов, Mismatch – степень несовместимости тканей.

Переменная Hospital представляет собой фиктивную группирующую переменную, которая показывает, к какой из трех больниц относится пациент.

Рандомизация

Рандомизация - формирование случайной выборки по исходной таблице данных.

Более подробное рассмотрение данного понятия дается здесь.

Из имеющихся данных будем выделять произвольные подмножества различными методами.

В меню Данные выберем команду Подмножество/Случайный выбор.

В этом диалоге находятся три вкладки: Простой выбор, Стратифицированный и Опции.

Вкладка Простой выбор

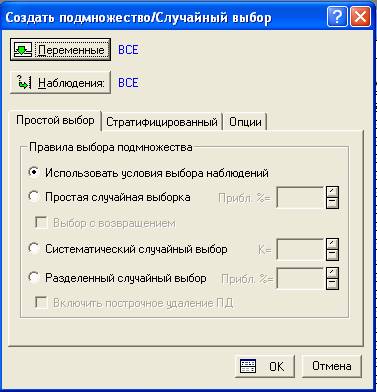
Рис 2. Создать подмножество/Случайный выбор, Вкладка Простой выбор

Выберем вкладку Простой выбор. Выбор может осуществляться по одному из следующих правил:

1) Использовать условия выбора наблюдений. Выберем переменные и определим условия выбора наблюдений в активном файле данных.

Предположим, что нас интересуют данные по больным, находящихся только в больнице ST_AND. Нажав кнопку Наблюдения, укажем заданное нами условие и нажмем OK.

Рис.3 Условия выбора наблюдений в Таблице данных

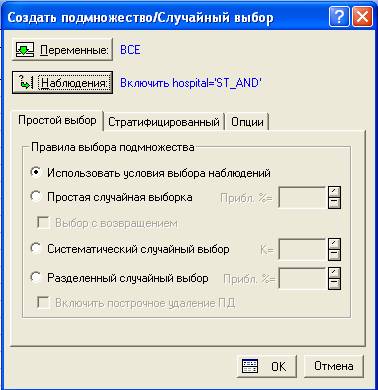
Рис. 4 Простой выбор, Использовать условия выбора наблюдений

В результате, получим данные, относящиеся только к интересующей нас больнице.

Рис. 5 Данные, относящиеся к больным, находившимся в больнице ST_AND

2) Простая случайная выборка. При выборе этого правила, данные будут выбираться случайным образом.

Существует два способа выбора подмножества в общей совокупности: указав процент наблюдений или указав приблизительное число наблюдений (данный параметр устанавливается в меню Опции). Предположим, мы хотим проанализировать 40% пациентов.

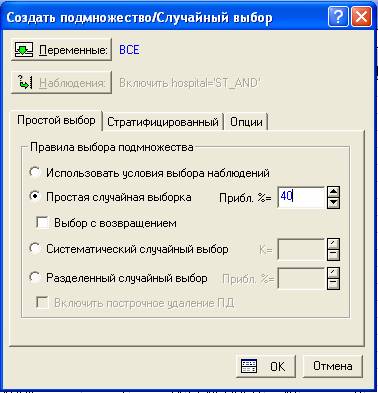
Рис. 6 Простая случайная выборка, 40% наблюдений

После нажатия кнопки OK, получим следующие результаты:

Рис. 7 Результаты простой случайной выборки, содержащей 40% наблюдений

Поставив флажок в поле Выбор с возвращением, получим следующий результат: при включении наблюдения в подмножество, это наблюдение снова попадает в исходное множество наблюдений (таким образом, одно наблюдение может встретиться несколько раз в итоговом подмножестве).

3) Систематический случайный выбор. Используя данный метод, подмножество будет составляться с помощью систематического случайного выбора.

Например, если ввести число 5 в поле K=, то среди первых пяти наблюдений будет случайным образом выбрано одно, а затем STATISTICA будет выбирать каждое пятое наблюдение в исходном множестве данных.

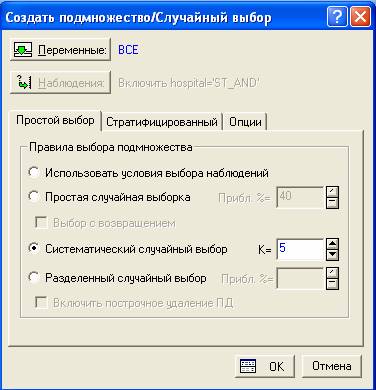
Рис. 8 Систематический случайный выбор, К=5

4) Разделенный случайный выбор. При выборе данного метода, все наблюдения будут случайным образом разделены на два файла данных. Необходимо указать процент наблюдений или приблизительное число наблюдений (данный параметр устанавливается в меню Опции).

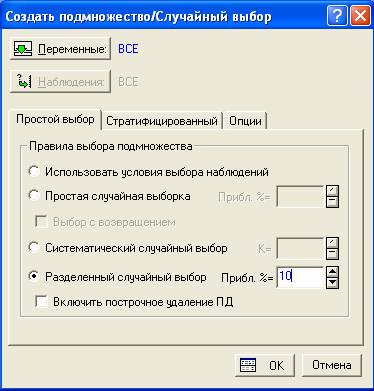
Рис.9 Разделенный случайный выбор, N=10

Вкладка Стратифицированный

С помощью данной опции будет создана стратифицированная случайная выборка на основе текущего файла данных. Можно указать несколько стратифицирующих переменных, которые содержат целочисленные кодовые значения, определяющие отдельные группы (страты).

Стратифицированная выборка будет построена на основе комбинации всех кодов во все стратифицирующих переменных.

Например, выбрав в качестве переменных расслоения CENSORED и HOSPITAL, будут созданы различные доли выборок для комбинаций COMPLETE-HILLVIEW, COMPLETE- ST_AND, COMPLETE- BINER, CENSORED-HILLVIEW, CENSORED-ST_AND, CENSORED-BINER.

Опция Равные вероятности отмечается для выбора одной и той же доли наблюдений во всех группах. Предположим, общий (для всех групп) процент наблюдений в выборках составляет 50% (возможно также задание приблизительного числа наблюдений).

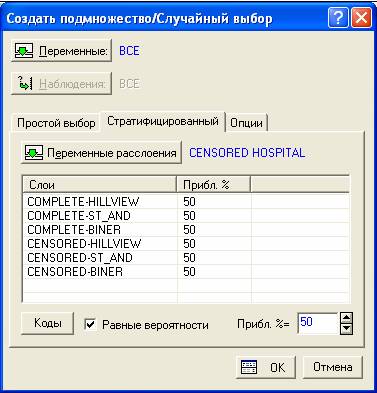
Рис. 10 Вкладка Стратифицированый

Вкладка Опции

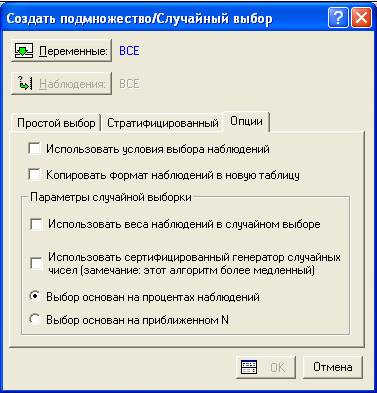
Рис. 11 Вкладка Опции

1) Использовать условия выбора наблюдений. Если вы выбрать эту опцию, то условия выбора наблюдений, заданные при нажатии кнопки Наблюдения в диалоге будут применяться перед созданием подмножества.

Чтобы игнорировать условия выбора наблюдений, следует убрать отметку этой опции

2) Копировать формат наблюдений в новую таблицу. Отметив эту опцию, формат ячеек будет копироваться в новое подмножество.

3) Использовать веса наблюдений в случайном выборе. Если в текущей Таблице данных заданы веса наблюдений, можно интерпретировать эти веса как множители наблюдений. В этом случае, соответствующая дробная выборка будет эффективно подогнана к весам наблюдений.

4) Использовать сертифицированный генератор случайных чисел. STATISTICA использует очень точный и качественный генератор случайных чисел в тех случаях, когда необходимо провести некоторые процедуры.

Однако в большинстве процедур случайного выбора или стратифицированного случайного выбора можно использовать более простые и быстрые методы случайного выбора наблюдений. В частности, при работе с очень большими файлами данных можно убрать отметку этой опции для ускорения работы.

5) Выбор основан на процентах наблюдений. При выборе этой опции файл данных разделяется на основе процента наблюдений.

6) Выбор основан на приближенном N. При выборе этой опции файл данных разделяется на основе числа наблюдений.

Мета-анализ

Введение

В соответствии с концепцией доказательной медицины научно обоснованными признаются результаты лишь тех клинических исследований, которые проведены на основе принципов клинической эпидемиологии, позволяющих свести к минимуму как систематические ошибки, так и случай¬ные ошибки (с помощью корректного статистического анализа полученных в исследовании данных).

Наиболее обоснованные результаты обычно могут быть получены при проведении рандомизированных контролируемых испытаний лечебных и профилактических вмешательств, так как в таких случаях организация (т.е. структура) и проведение исследования наиболее близки к эксперименту в общенаучном понимании этого термина.

Достаточно часто результаты исследований, в которых оценивается эффективность одного и того же лечебного или профилактического вмешательства или диагностического метода при одном и том же заболевании, различаются.

В связи с этим возникает необходимость относительной оценки результатов разных исследований и интеграции их результатов с целью получения обобщающего вывода.

К одной из самых популярных и быстро развивающихся методик системной интеграции результатов отдельных научных исследований сегодня относится методика мета-анализа.

Международная эпидемиологическая ассоциация характеризует мета-анализ как методику "объединения результатов различных исследований, …складывающуюся из качественно го компонента (например, использование таких заранее определенных критериев включения в анализ, как полнота данных, отсутствие явных недостатков в организации исследования и т.д.) и количественного компонента (статистическая обработка имеющихся данных)".

Цель мета-анализа — выявление, изучение и объяснение различий (вследствие наличия статистической неоднородности, или гетерогенности) в результатах исследований.

К несомненным преимуществам мета-анализа относятся возможность увеличения статистической мощности исследования, а, следовательно, точности оценки эффекта анализируемого вмешательства. Это позволяет более точно, чем при анализе каждого отдельно взятого небольшого клинического исследования, определить категории больных, для которых применимы полученные результаты.

Правильно выполненный мета-анализ предполагает проверку научной гипотезы, подробное и четкое изложение применявшихся при мета-анализe статистических методов, достаточно подробное изложение и обсуждение результатов анализа, а также вытекающих из него выводов.

Подобный подход обеспечивает уменьшение вероятности случайных и систематических ошибок, позволяет говорить об объективности получаемых результатов.

Подходы к выполнению мета-анализа

Существуют два основных подхода к выполнению мета-анализа.

Первый из них заключается в статистическом повторном анализе отдельных исследований путем сбора первичных данных о включенных в оригинальные исследования наблюдениях. Очевидно, что проведение данной операции далеко не всегда возможно.

Второй (и основной) подход заключается в обобщении опубликованных результатов исследований, посвященных одной проблеме. Такой мета-анализ выполняется обычно в несколько этапов, среди которых важнейшими являются:

• выработка критериев включения оригинальных исследований в мета-анализ

• оценка гетерогенности (статистической неоднородности) результатов оригинальных исследований

• проведение собственно мета-анализа (получение обобщенной оценки величины эффекта)

• анализ чувствительности выводов

Необходимо отметить, что этап определения круга включаемых в мета-анализ исследований часто становится источником систематических ошибок мета-анализа. Качество мета-анализа существенно зависит от качества включенных в него исходных исследований и статей.

К основным проблемам при включении исследований в мета-анализ относятся такие, как различия исследований по критериям включения и исключения, структуре исследования, контролю качества.

Существует также смещение, связанное с преимущественным опубликованием положительных результатов исследования (исследования, в которых получены статистически значимые результаты, чаще публикуются, чем те, в которых такие результаты не получены).

Поскольку мета-анализ основан главным образом на опубликованных данных, следует обращать особое внимание на недостаточную репрезентативность отрицательных результатов в литературе.

Включение в мета-анализ неопубликованных результатов также представляет значительную проблему, так как их качество неизвестно в связи с тем, что они не проходили рецензирование.

Основные методы

Выбор метода анализа определяется типом анализируемых данных (бинарные или непрерывные) и типом модели (фиксированных эффектов, случайных эффектов).

Бинарные данные обычно анализируются путем вычисления отношения шансов (ОШ), относительного риска (ОР) или разности рисков в сопоставляемых выборках. Все перечисленные показатели характеризуют эффект вмешательств. Представление бинарных данных в виде ОШ удобно использовать при статистическом анализе, но этот показатель достаточно трудно интерпретировать клинически.

Непрерывными данными обычно являются диапазоны значений изучаемых признаков или нестандартизованная разница взвешенных средних в группах сравнения, если исходы оценивались во всех исследованиях одинаковым образом.

Если же исходы оценивались по-разному (например, по разным шкалам), то используется стандартизованная разница средних (так называемая величина эффекта) в сравниваемых группах.

Одним из первых этапов мета-анализа является оценка гетерогенности (статистической неоднородности) результатов эффекта вмешательства в разных исследованиях.

Для оценки гетерогенности часто используют критерии χ2 с нулевой гипотезой о равном эффекте во всех исследованиях и с уровнем значимости 0,1 для повышения статистической мощности (чувствительности) теста.

Источниками гетерогенности результатов разных исследований принято считать дисперсию внутри исследований (обусловленную случайными отклонениями результатов разных исследовании от единого истинного фиксированного значения эффекта), а также дисперсию между исследованиями (обусловленную различиями между изучаемыми выборками по характеристикам больных, заболеваний, вмешательств, приводящими к несколько разным значениям эффекта — случайными эффектами).

Если предполагается, что дисперсия между исследованиями близка к нулю, то каждому из исследований приписывается вес, величина которого обратно пропорциональна дисперсии результата данного исследования.

Дисперсия внутри исследований в свою очередь определяется как , где - - среднее внутри исследований.

При нулевой дисперсии между исследованиями можно использовать модель фиксированных (постоянных) эффектов. В этом случае предполагается, что изучаемое вмешательство во всех исследованиях имеет одну и ту же эффективность, а выявляемые различия между исследованиями обусловлены только дисперсией внутри исследований. В этой модели пользуются методом Мантела-Ханзела.