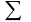3.2.Аналіз реалізації молока методом множинної кореляції. Порядок обчислення рівняння множинної лінійної регресії, характеристика показників тісноти зв’язку.

Кореляцію, за допомогою якої вивчається вплив на результативну ознаку двох і більше взаємопов’язаних факторних ознак, називають множинною. При вивченні множинної кореляції можна застосовувати як прямолінійні, так і криволінійні рівняння регресії.

Багатофакторні регресійні моделі дають змогу оцінювати вплив на досліджувану результативну ознаку кожного окремого із включе­них у рівняння факторів при фіксованому значенні (на середньому рівні) інших факторів. При цьому важливою умовою множинної коре­ляції є відсутність функціонального зв'язку між факторами.

Важливе значення при множинній кореляції має вибір форми зв'язку і відповідного математичного рівняння множинної регресії. Вибір типу функції має ґрунтуватися на теоретичному аналізі дослі­джуваного явища або на досвіді попередніх аналогічних досліджень. Враховуючи, що будь-яку функцію багатьох змінних можна звести до лінійного виду логарифмуванням, рівняння множинної регресії частіше будують у лінійній формі.

Формула лінійного рівняння множинної регресії має такий вигляд:

у_х = а₀ + а₁х₁+а₂х₂

де Yх — теоретичні значення результативної ознаки;

а₀, а₁ а₂—параметри рівняння;

х₁, х_2,х₃—факторні ознаки.

Окремі коефіцієнти регресії цього рівняння характеризують вплив відповідного фактора на результативний показник при фіксованому (елімінованому) значенні інших факторів. Вони показують, наскіль­ки змінюється результативний показник при зміні відповідного фак­тора на одиницю. Вільний член рівняння (а₀) не має економічного зміс­ту і не інтерпретується.

Параметри рівняння множинної регресії обчислюють способом найменших квадратів розв'язанням системи рівнянь:

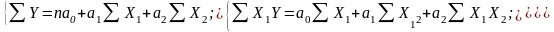
Показниками щільності зв’язку при множинній кореляції використовують такі: парні, часткові і множинні (сукупні) коефіцієнти кореляції і множинний коефіцієнт детермінації.

Парні коефіцієнти кореляції використовують для вимі­рювання щільності зв'язку між двома досліджуваними ознаками без урахування їх взаємодії з іншими ознаками, включеними у кореляційну модель.

; ;

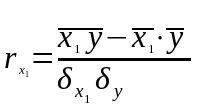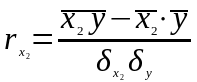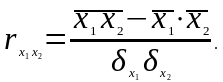
Часткові коефіцієнти кореляції характеризують щіль­ність зв'язку результативної ознаки з однією факторною ознакою при умові, що інші факторні ознаки перебувають на постійному рівні. Парний коефіцієнт кореляції між результативною і факторною ознаками, як правило, не дорівнює відповідному частковому коефіцієнту.

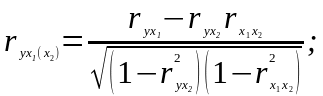
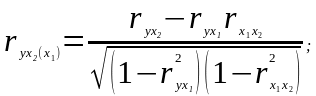
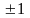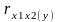Коефіцієнт може приймати значення від 0 до . При >0 зв’язок між ознаками прямий, при <0 зв’язок між ознаками зворотній.

Коефіцієнти часткової кореляції дозволяють встановити “чистий” вплив кожного окремого фактора або ознаки на інші ознаки, що враховуються. Тобто визначають тісноту зв’язку між двома ознаками (наприклад, 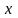₁ і х₂) при виключенні впливу інших факторів (в нашому випадку ).

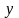Щоб обчислити тісноту зв’язку між двома ознаками х₁ і при виключенні впливу х₂ потрібно в формулі поміняти місцями і х₂.

Тіснота зв’язку між трьома ознаками 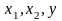визначається і за допомогою коефіцієнтів множинної кореляції . Тоді можна визначити, наприклад, міру залежності між ознакою у та сукупністю ознак 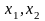(позначимо 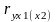). Обчислення проводяться за формулою:

.

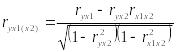Повні коефіцієнти кореляції приймають значення від 0 до 1.

Коефіцієнт множинної (сукупної) детермінації показує, яка частка варіації досліджуваного результативного по­казника зумовлена впливом факторів, включених у рів­няння множинної регресії.

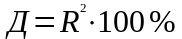
Він може мати значення від О до +1. Чим ближчий коефіцієнт множинної детермінації до одиниці, тим більше варіація результативного показника характеризується впливом відібраних факторів.

Множинний коефіцієнт кореляції, характеризує тісноту зв’язку між всіма досліджуваними у моделі ознаками:

.

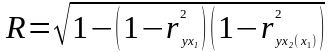Чим більш прямолінійною є залежність, тим більш множинний коефіцієнт кореляції відповідає індексу кореляції.

У свою чергу множинний коефіцієнт детермінації розкладають на часткові коефіцієнти детермінації, які характеризують на скільки відсотків варіація результативної ознаки залежить від варіації кожної з факторних ознак.

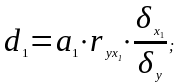
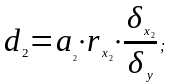
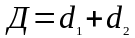
У множинній кореляції обчислюють також коефіцієнт еластичності та β- коефіцієнт.

Коефіцієнт еластичності ( показує на скільки процентів зміниться результативний показник при зміні факторного на 1 %).

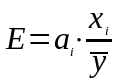
β- коефіцієнт (показує на скільки квадратичних відхилень змінюється результативний показник при зміні факторної ознаки на 1 середнє квадратичне відхилення)

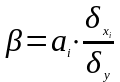
Перевірку істотності зв'язку здійснюють за допомо­гою F- критерію та коефіцієнтів детермінації.

:

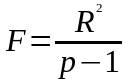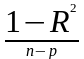
Перевірка суттєвості регресії здійснюють за формулою:

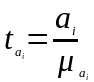, де

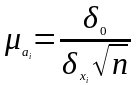
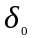- характеризує вплив факторів, які не досліджуються в моделі і обчислюється:

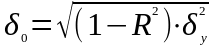
Розрахункова частина до 3.2.:

Виходячи з методу найменших квадратів, запишемо систему нормальних рівнянь, для реалізаційної ціни молока (Y), обсягу молока (Х₁) та виручки від реалізації молока (Х₂).

Вихідні та розрахункові дані для аналізу множинної лінійної кореляції. Таблиця 3.2.

	№		Обсяг продукції, тис.т., х1		Ціна молока, грн., у		Виручка від молока, млн.грн.,х2		ух2		X12		x22		x1x2				Y(x)
	1		532,8		1611,9		858,82		1384332,47		283875,8		737572,34		457579,5		2598222		594620,7
	2		103,5		1734,8		179,55		311486,46		10712,25		32238,84		18583,61		3009531		-307447
	3		467,8		1644,8		769,43		1265570,7		218836,8		592033,97		359942,8		2705367		466713,9
	4		362,1		1734,2		627,95		1088997,51		131116,4		394326,00		227382,1		3007450		261209,1
	5		128,1		1395,6		178,77		249500,28		16409,61		31960,98		22901,25		1947699		-281333
	6		283,8		1533,9		435,32		667738,60		80542,44		189504,21		123544		2352849		52393,73
	7		113,5		1292,7		146,72		189666,81		12882,25		21527,183		16652,88		1671073		-317780
	8		435,9		1567,6		683,31		1071167,48		190008,8		466921,90		297857,8		2457370		376718,6
	9		338,9		1386,9		470,02		651871,30		114853,2		220919,18		159289,9		1923492		134359,8
	11		232,9		1534,9		357,47		548693,30		54242,41		127790,67		83256,68		2355918		-52823,8
	12		143		1585,8		226,76		359610,91		20449		51424,36		32428,02		2514762		-234293
	13		418,4		1528,3		639,44		977257,25		175058,6		408884,43		267542		2335701		329518,4
	14		328,1		1620,6		531,71		861703,58		107649,6		282724,94		174457		2626344		162425,5
	15		241		1383,8		333,49		461491,48		58081		111219,44		80372,49		1914902		-59511,7
	16		218,4		1823,3		398,20		726053,95		47698,56		158570,18		86968,78		3324423		-42269,8
	17		140,9		1609,6		226,79		365045,43		19852,81		51434,90		31955,08		2590812		-236550
	18		118		1687,2		199,08		335903,97		13924		39636,66		23492,57		2846644		-279173
		19		424,9		1697,2		721,14		1223919,28		180540		520043,30		306412,5		2880488		389186,2
		20		137,3		1694		232,58		394001,023		18851,29		54096,34		31934,09		2869636		-236713
		21		320		1623,3		519,45		843232,925		102400		269834,53		166225,9		2635103		145762
		22		282,1		1609,4		454,01		730686,494		79580,41		206126,66		128076,7		2590168		62596,3
		23		164,1		1812,1		297,36		538856,22		26928,81		88426,30		48797,7		3283706		-165984
		24		117,8		1565,4		184,40		288666,209		13876,84		34004,87		21722,8		2450477		-288851
		25		136,6		1617,6		220,96		357431,625		18659,56		48825,16		30183,7		2616630		-244957
		ξ		6364,8		40467		10193,01		16408205,8		2027621		5230176,99		3250068		64455139		75353,2
		/25		254,59		1618,6		407,72		656328,23		81104,82		209207,08		130002,7		2578206		3014,13

Лінійне рівняння регресії для множинної кореляційної моделі має вигляд:

,

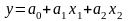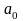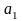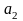Для знаходження коефіцієнтів , і множинної кореляції розв’язуємо таку систему рівнянь:

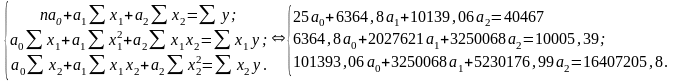Розв’язавши дану систему рівнянь маємо:

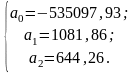
Отже, рівняння множинної регресії, яке характеризує залежність надою на корову від витрат кормів та виходу приплоду , матиме такий вигляд:

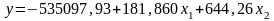
Знайдені коефіцієнти регресії показують, наскільки зміниться ціна на молоко при зміні відповідного фактора на одиницю при умові, що другий фактор, включений у рівняння, перебуває на середньому рівні. Так, 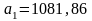показує, що при середньому обсязі реалізації молока збільшення виручки реалізованого молока сприятиме зростанню ціні молока на 1081,86грн.

Обчислюємо:

1) парні коефіцієнти кореляції , , ,

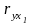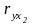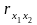Виходячи з попередніх розрахунків, де 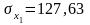та 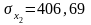, та використовуючи дані з таблиці 3.2., маємо:

а) ,

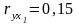б) ,

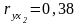в)

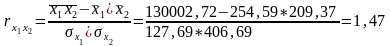
2) часткові коефіцієнти кореляції:

а)

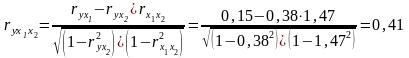
б)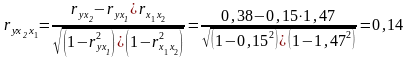

3) множинний коефіцієнт кореляції:

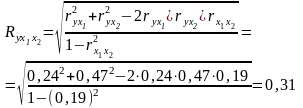
4) коефіцієнт множинної детермінації:

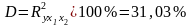
5) часткові коефіцієнти детермінації:

а)

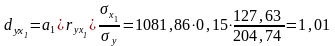
б)

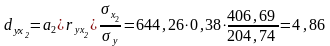
6) Перевірка суттєвості коефіцієнтів кореляції

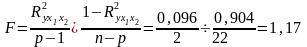
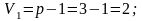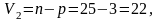при та де 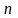- кількість одиниць спостереження; 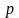- кількість параметрів у рівнянні.

при ступенів свободи 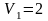та 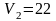дорівнює 1,17.

Отже, так як фактичне значення перевищує теоретичне, то можна сказати про існування істотного зв’язку між даними параметрами рівняння, тобто зв’язок між обсягом реалізованого молока та виручкою від реалізації досить великий.

3.3.Непараметричні критерії кореляційних зв’язків ( рангова кореляція)

Якщо характер розподілу досліджуваної сукупності навіть передбачувані неві­домі, то тісноту зв'язку можна обчислити за допомогою непараметричних критеріїв визначення тісноти зв'язку.

Особливістю цих критеріїв є те, що тіснота зв'язку між ознаками визначається не за кількісними значеннями варіантів, а за допомогою порівняння їх рангів.

Під рангом розуміють порядковий номер оди­ниці сукупності в ранжируваному ряду розподілу. Чим менші розбіж­ності між рангами, тим тісніший зв'язок між ознаками. До непараметричних критеріїв показників тісноти зв'язку відно­сяться коефіцієнти: кореляції рангів, знаків Фехнера, асоціації, контингенції та ін.

Коефіцієнт Фехнера застосовується для оцінки тісноти зв'язку на основі порівнянь знаків відхилень значень результативної і факторної ознак від їх середніх, його обчислюють за формулою:

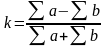
де Σа – сума збігів знаків; Σb – сума незбігів знаків.

Коефіцієнт Фехнера змінюється від 0 до ±1. Якщо знаки всіх від­хилень збігаються, то Σb=0, а коефіцієнт Фехнера дорівнює одиниці, що свідчить про наявність прямого зв'язку. Якщо і знаки всіх відхи­лень будуть різними, то Σа=0, а коефіцієнт Фехнера дорівнює - 1, що вказує на наявність оберненого зв'язку.

Слід мати на увазі, що коефіцієнт Фехнера тільки констатує на­явність і напрям кореляційного зв'язку і не залежить від величини відхилень результативної і факторної ознак від відповідних середніх, у зв'язку з чим оцінка тісноти зв'язку є наближеною. Коефіцієнт Фех­нера може бути деяким орієнтиром в оцінці інтенсивності зв'язку.

Коефіцієнт кореляції рангів – це один з найпростіших показників тісноти зв'язку (його ще називають ранговим коефіцієнтом кореляції Спірмена). Взаємозв’язок між ознаками, які можна зранжувати, передусім на основі бальних оцінок, вимірюється методами рангової кореляції. Рангами називають числа натурального ряду, які згідно зі значеннями ознаки надаються елементам сукупності і певним чином упоряд­ковують її. Ранжування проводиться за кожною ознакою окремо: перший ранг надається найменшому значенню ознаки, останній — найбільшому.

Кількість рангів дорівнює обсягу сукупності. Очевидно, зі збільшенням обсягу сукупності ступінь «розпізнаваності» елементів зменшується. З огляду на те, що рангова кореляція не потребує додержання будь-яких математичних передумов щодо розподілу ознак, зокрема вимоги нормальності розподілу, рангові оцінки щільності зв’язку доцільно використовувати для сукупнос­тей невеликого обсягу.

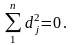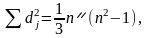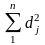Ранги, надані елементам сукупності за ознаками Х і У, позначають відповідно R_x та R_y. Залежно від ступеня зв’язку між ознаками певним чином співвідносяться й ранги. При прямому функціональному зв’язку R_x = R_y, тобто відхилення між рангами d=R_x -R_y=0. отже, й сума квадратів відхилень При зворотному функціональному зв’язку де n — число рангів. Якщо зв’язок між ознаками відсутній, являє собою середню арифметичну цих крайніх значень:

.

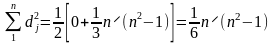Це є максимальна сума квадратів відхилень рангів. Отже, за відсутності зв’язку:

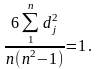
Спираючись на зазначену математичну тотожність, К. Спірмен запропонував формулу для коефіцієнта рангової кореляції:

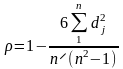
Коефіцієнт рангової кореляції має такі самі властивості, як і лінійний коефіцієнт кореляції: змінюється в межах від –1 до +1, водночас оцінює щільність зв’язку та вказує на його напрям. Для варіантів, які повторюються, ранг визначається як середня арифметична відповідних рангів.

Розрахункова частина до 3.3.:

Обчислимо коефіцієнт кореляції рангів. Розрахунки проведемо в таблиці 3.3. і підставимо в формулу коефіцієнта кореляції рангів.

Розрахунок коефіцієнта рангової кореляції.

Таблиця 3.3.

№	Обсяг молока, тис.т., х1	Ціна молока, грн., у	Виручка від реалізації молока, млн.грн.,х2	Ранги
				Rх1	Rx2	Ry	d1	d2	d12	d22
1	532,8	1611,9	858,82	25	25	13	12	12	144	144
2	103,5	1734,8	179,55	1	3	23	-22	-20	484	400
3	467,8	1644,8	769,43	24	24	17	7	7	49	49
4	362,1	1734,2	627,95	20	20	22	-2	-2	4	4
5	128,1	1395,6	178,77	5	2	4	1	-2	1	4
6	283,8	1533,9	435,32	16	15	6	10	9	100	81
7	113,5	1292,7	146,72	2	1	1	1	0	1	0
8	435,9	1567,6	683,31	23	22	9	14	13	196	169
9	338,9	1386,9	470,02	19	17	2	17	15	289	225
10	174,9	1716,5	300,25	11	11	21	-10	-10	100	100
11	232,9	1534,9	357,47	13	13	7	6	6	36	36
12	143	1585,8	226,76	9	7	10	-1	-3	1	9
13	418,4	1528,3	639,44	21	21	5	16	16	256	256
14	328,1	1620,6	531,71	18	19	15	3	4	9	16
15	241	1383,8	333,49	14	12	3	11	9	121	81
16	218,4	1823,3	398,20	12	14	25	-13	-11	169	121
17	140,9	1609,6	226,79	8	8	12	-4	-4	16	16
18	118	1687,2	199,08	4	5	18	-14	-13	196	169
19	424,9	1697,2	721,14	22	23	20	2	3	4	9
20	137,3	1694	232,58	7	9	19	-12	-10	144	100
21	320	1623,3	519,45	17	18	16	1	2	1	4
22	282,1	1609,4	454,01	15	16	11	4	5	16	25
23	164,1	1812,1	297,36	10	10	24	-14	-14	196	196
24	117,8	1565,4	184,40	3	4	8	-5	-4	25	16
25	136,6	1617,6	220,96	6	6	14	-8	-8	64	64
	6364,8	40467	10193,1	-	-	-	0	0	2622	2294

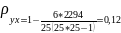
Одержаний додатній коефіцієнт кореляції рангів свідчить про прямий, помітний зв’язок між ціною молока та обсягом молока і виручкою молока.