- •«Братский государственный университет»
- •С одержание
- •1. Аналитическая часть
- •1.1 Метод предельных состояний
- •1.2 Расчетное сопротивление и модуль упругости конструктивных материалов
- •2.1 Расчет сжатых элементов.
- •Запас прочности равен 83,2 %, т.Е стенка имеет значительный запас прочности на срез. Прочность принятого сечения балки в виде прокатного двутавра обеспечена.
- •4. Рассчитаем себестоимость балки из древесины.
- •Список использованных источников
1.2 Расчетное сопротивление и модуль упругости конструктивных материалов
При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала.
Расчетное сопротивление приведено в СНиП. Оно определяется в соответствии с ГОСТ: испытание стандартных образцов в лабораторных условиях на испытательных машинах, уставленных в соответствии с ГОСТ.
В результате испытания образца материала определяется его предел прочности – Rпр.пр. величина нормативного расчетного сопротивления (Rн) определяется в результате многократных испытаний (большого количества образцов) с учетом анализа статических показателей (с.к.о., коэффициент вариации, доверительный интервал) и индивидуальных свойств материала (пороки древесины, неоднородность структуры бетона и др.) рассчитывается по формуле:
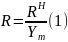
где
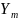 – коэффициент безопасности по материалам,
– коэффициент безопасности по материалам,
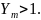
 Если
Если
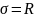 ,
то такое состояние называется предельным
– состояние, за пределами которого
нормальная эксплуатация невозможна.
,
то такое состояние называется предельным
– состояние, за пределами которого
нормальная эксплуатация невозможна.
Под упругостью древесины понимают её способность сопротивляться изменению формы или объёма под воздействием механических напряжений.
При кратковременных нагрузках до напряжений, соответствующих пределу пропорциональности (т.е. до момента необратимости деформации) деформация древесины пропорциональна напряжению и исчезает после снятия нагрузки.
Основными показателями упругости древесины являются модуль упругости, модуль сдвига, и коэффициент деформации. Испытания проводят на малых образцах с чистой древесиной, по направлениям: вдоль волокон, радиально поперёк волокон, тангенциально поперёк волокон.
Например модуль упругости на статический изгиб у сосны- 12,6 ГПа, у ели- 11,0 ГПа, у берёзы- 15,4 ГПа, у дуба- 15,4 ГПа[5].
2.1 Расчет сжатых элементов.
Задача №1
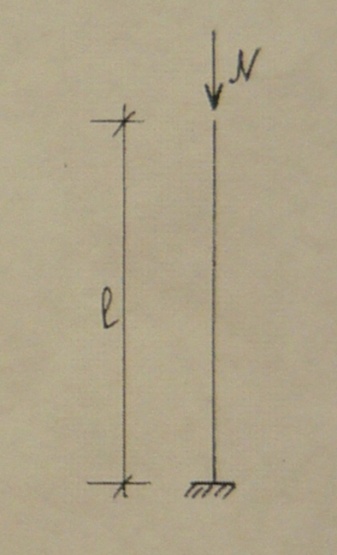 Подобрать
сечение стойки из древесины сосны 1
сорта; расчетная схема которой приведена
на рисунке; высота стойки l
=3,0 м, продольная сила в стержне стойки;
N=220
кН; предельная гибкость
Подобрать
сечение стойки из древесины сосны 1
сорта; расчетная схема которой приведена
на рисунке; высота стойки l
=3,0 м, продольная сила в стержне стойки;
N=220
кН; предельная гибкость
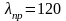 .
.
Решение:
Расчетное
сопротивление древесины сжатию
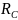 =
1,4 кН
=
1,4 кН
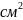 (I
сорт);
(I
сорт);
Коэффициент
приведения расчетной длины
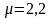 расчетной длины.
расчетной длины.

Формулы:
Условие прочности бруса, работающего на осевое сжатие, рассчитывается по формуле:
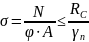 ,
(1)
,
(1)
где N – продольное усилие [кН];
Арасч. – учитывает все возможные ослабления для древесины (деревянные элементы, работающие на растяжение могут быть из древесины только первого сорта: Арасч. ≥ 50 см2) [м2];
R – расчетное сопротивление [кН/м ];
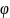 – коэффициент
устойчивости или коэффициент продольного
изгиба. Рассчитывается по формуле:
– коэффициент
устойчивости или коэффициент продольного
изгиба. Рассчитывается по формуле:
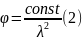
где
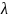 – гибкость элемента;
– гибкость элемента;
const – устанавливается в зависимости от материала (древесина – 3000; фанера – 2500; стеклопластик – 986). Гибкость рассчитывается по формуле:
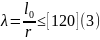
где
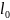 -
расчетная длина:
-
расчетная длина:
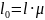 ,
,

 – радиус
инерции сечения:
– радиус
инерции сечения:

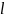 -
номинальная длина;
-
номинальная длина;
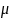 -
коэффициент приведения к расчетной
длине с учетом закрепления концов
элемента (шарнирная заделка –
-
коэффициент приведения к расчетной
длине с учетом закрепления концов
элемента (шарнирная заделка –
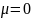 ;
жесткая заделка –
;
жесткая заделка –
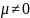 ).
).
Решение:
Записанное условие (1) позволяет производить три вида расчета на прочность:
Подбор сечения. Для этого из условия (1) выразим “А”, получим:

Подставим
значения: N
= 220 кН; значение
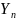 возьмем для II
класса ответственности, равный 0,95
(жилые, общественные и промышленные
здания); так как у нас древесина I
сорта, то
возьмем для II
класса ответственности, равный 0,95
(жилые, общественные и промышленные
здания); так как у нас древесина I
сорта, то
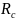 = 14 МПа = 1,4кн/см2
для неклеёной древесины, расчетное
значение
определяем по формуле (2). В
случае расчёта сжатых элементов
целесообразно задаться гибкостью.
= 14 МПа = 1,4кн/см2
для неклеёной древесины, расчетное
значение
определяем по формуле (2). В
случае расчёта сжатых элементов
целесообразно задаться гибкостью.
Пусть
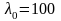
Определяем коэффициент продольного изгиба
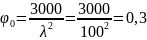
Тогда требуемая площадь сечения из условия общей устойчивости
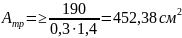
Теперь можно найти ширину сечения, для этого извлечем квадратный корень из полученного значения площади:
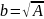
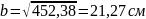
 По
допускаемым поперечным размерам бруса
и допускаемому напряжению материала
устанавливают значение допускаемой
продольной силы. Для этого нам потребуется
определить: фактическое значение
коэффициента устойчивости по формуле
(2), фактическое значение гибкости
элемента по формуле (3), расчетную длину
по формуле (3) и радиус инерции сечения
по формуле (4). Длина бруса = 3,0 м или 300
см; коэффициент приведения к расчетной
длине с учетом закрепления концов
элемента равен 2,2.
По
допускаемым поперечным размерам бруса
и допускаемому напряжению материала
устанавливают значение допускаемой
продольной силы. Для этого нам потребуется
определить: фактическое значение
коэффициента устойчивости по формуле
(2), фактическое значение гибкости
элемента по формуле (3), расчетную длину
по формуле (3) и радиус инерции сечения
по формуле (4). Длина бруса = 3,0 м или 300
см; коэффициент приведения к расчетной
длине с учетом закрепления концов
элемента равен 2,2.
Принимаем квадратное сечение стойки со стороной b=22 см
Тогда фактическая площадь стойки
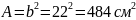
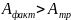
Радиус инерции сечения
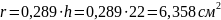
 Фактическая
гибкость
Фактическая
гибкость
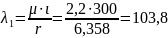
103,8 < 120
103,8
> 70
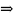
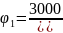 =
0, 28
=
0, 28
Проверим устойчивость стойки квадратного сечения со стороной b= 22 см по формуле:
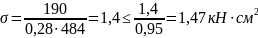
Следовательно, устойчивость центрально сжатой стойки квадратного сечения со стороной b= 22 обеспечена.
Определим нагрузку, которую может выдержать конструкция
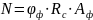
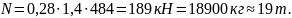
значение
полученной прочности (19 т) и заданного
значения прочности (22 т)
 отличаются
не существенно. Запас прочности составляет
18 %.
отличаются
не существенно. Запас прочности составляет
18 %.
Вывод данная конструкция является устойчивой и может выдержать заданную нагрузку.
Задача 2.2 Расчет изгибаемых элементов
Н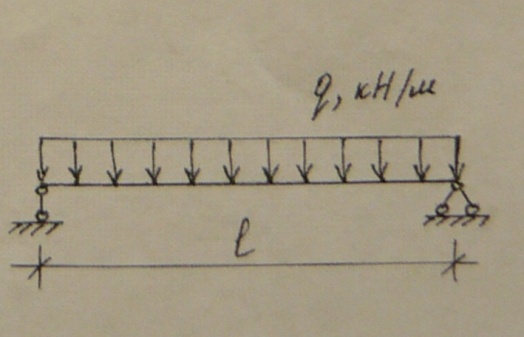 агрузка
q=5,2
кН/м = 0,052 кН/см
агрузка
q=5,2
кН/м = 0,052 кН/см
Длина l=5,5 м = 550 см.
Для заданной схемы балки требуется:
1. Построить эпюры «Q» и «M»;
2. Подобрать поперечное сечение прямоугольной формы с соотношением сторон h/b=2,8 из хвойной древесины, выполнить проверку по I, II группам предельного состояния;
3. Подобрать сечения из стального прокатного двутавра, выполнить проверку по I группе предельного состояния;
4. Определить себестоимость балки из древесины (цены 2012 г.).
Формулы:
Поперечная сила на опоре (Q) рассчитывается по формуле:
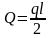 (5)
(5)
где q – расчетная нагрузка.
 Изгибающий
момент (Эп “M”)
по формуле:
Изгибающий
момент (Эп “M”)
по формуле:
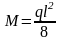 (6)
(6)
Изгибающие моменты рассчитываются по I и II группам предельных состояний.
Для
первой группы, подвергающимся нормальным
напряжениям (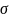 ),
делается проверка общей устойчивости,
она рассчитывается по формуле:
),
делается проверка общей устойчивости,
она рассчитывается по формуле:
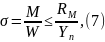
где W – момент сопротивления сечения [см3], определяется по формуле :
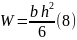
Так же рассчитывают значение местной устойчивости по формуле:
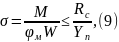
где
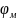 – коэффициент местной устойчивости,
находиться по формуле:
– коэффициент местной устойчивости,
находиться по формуле:
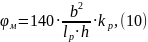
где h – высота в рассматриваемом сечении [м];
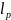 – расстояние
между точками закрепления сжатой верхней
кромки балки [м];
– расстояние
между точками закрепления сжатой верхней
кромки балки [м];
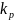 – коэффициент
формы эпюры моментов на рассматриваемом
участке (определяется по таблице).
– коэффициент
формы эпюры моментов на рассматриваемом
участке (определяется по таблице).
Для касательного напряжения используется формула Журавского:
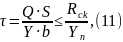
где
S
– статический момент сечения [см3]:
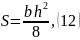
Y – момент инерции сечения [см4]:
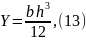

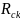 – расчетное
сопротивление скалыванию
– расчетное
сопротивление скалыванию
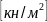 .
.
Для второй группы рассчитывается значение прогиба:
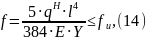
где 5/384 – коэффициент соответствующий расчетной схеме;
E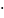 Y
– жесткость балки;
Y
– жесткость балки;
 Предельное
значение прогиба будет зависеть от
номинальной длины, т.е. если
Предельное
значение прогиба будет зависеть от
номинальной длины, т.е. если
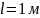 ,
то
,
то
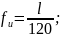 если
если
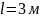 ,
то
,
то
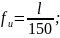 Интерполяция[4] -
это способ вычислить промежуточное
значение функции по нескольким уже
известным ее значениям.
Интерполяция[4] -
это способ вычислить промежуточное
значение функции по нескольким уже
известным ее значениям.
Решение:
1. Вначале постоим эпюры «М» и «Q», для этого найдем поперечную силу и изгибающий момент, соответственно по формулам 5 и 6:
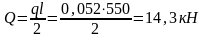
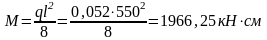
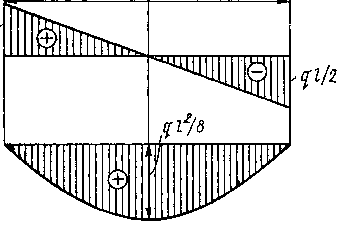
2. Теперь подберем сечение прямоугольной формы. Сначала найдем момент сопротивления сечения по формуле (7):
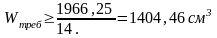
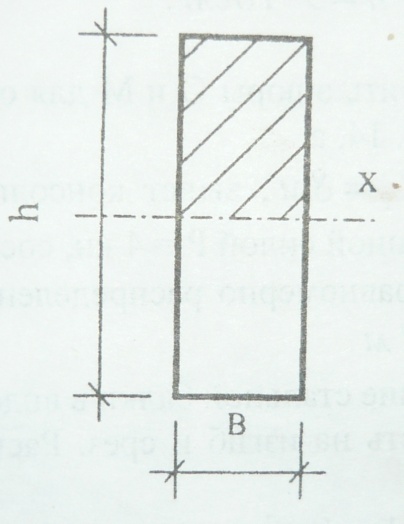
Принимаем прямоугольное сечение балки с соотношением сторон h:b =2,8.
h=2,8 b
Момент сопротивления прямоугольного сечения
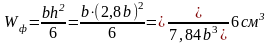 ,
,
 Приравниваем
Приравниваем
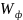 к
к
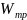 и
определяем требуемую ширину сечения :
и
определяем требуемую ширину сечения :
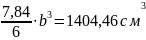
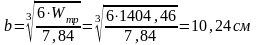 .
.
Округляем
значение b=
11 см и
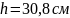 .
.
Определяем геометрические характеристики сечения:
площадь
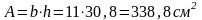 ;
;
момент сопротивления
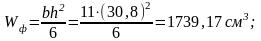
Требуемое значение момента сопротивления сечения меньше фактического 1739,17>1404,46.
Поперечное сечение для балки: b=11 см; h = 30,8с м. условие соблюдено.
Теперь выполним проверку по предельным состояниям:
по I группе :
а) по нормальным напряжениям (на изгиб)
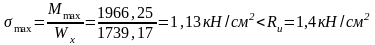
б) по касательным напряжениям (на скалывание)
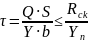
Статический момент половины сечения балки
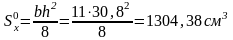
Момент инерции
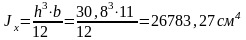
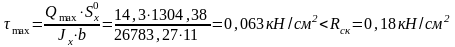
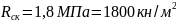
 Рассчитываем
по II
группе предельных состояний используя
формулу 14:
Рассчитываем
по II
группе предельных состояний используя
формулу 14:
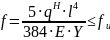
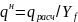
Коэффициент
надёжности по нагрузке для деревянных
конструкций
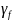 =1,1.
=1,1.
Следовательно, нормативная нагрузка равна:
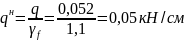
Е = 10000МПа = 1000 · 104 кН/м
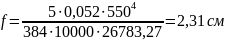
для нахождения предельного изгиба используем линейную интерполяцию:
L |
fu |
3 |
0,02 |
5,6 |
х |
6 |
0,3 |
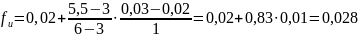
f
= 2, 31 <
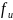 = 2, 80 см
= 2, 80 см
Данная
балка прошла проверку по всем группам
предельных состояний. Максимальная
нагрузка, которую cможет
выдержать балка, не деформируясь, равна
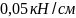 .
.
 3.
Подберем сечение из стального прокатного
двутавра.
3.
Подберем сечение из стального прокатного
двутавра.

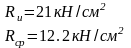
 Из
условия прочности на изгиб определяем
требуемый момент сопротивления сечения:
Из
условия прочности на изгиб определяем
требуемый момент сопротивления сечения:
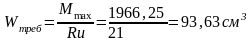
Принимаем двутавр № 16:
Wx=109 cм3 > Wтреб=93,63 см3
Так как подобранное сечение требуется проверить на срез, нам потребуются следующие данные:
Sx=62,3 см3, Jx= 873см4, tст =d=5,0 мм =0,5 см.
Проверка прочности подобранного сечения:
а) по нормальным напряжениям (на изгиб)
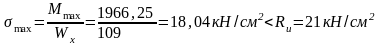
б) по касательным напряжениям: