
- •Содержание
- •Упрощение заданного выражения алгебры множеств
- •Анализ заданного бинарного отношения
- •Минимизация пополненной функции с помощью карт
- •Введение
- •Задание №1
- •Выбор варианта выражения алгебры множеств
- •Вычисляем вариант для таблицы операций:
- •Соответственно отсюда:
- •Минимизация полученного выражения
- •2.1. Выбор варианта бинарного отношения
- •Бинарное отношение
- •Построение графика
- •Исследование свойств отношения
- •Свойства отношения внесены в таблицу:
- •Задание №3 Минимизация пополненной функции с помощью карт
- •Литература:
Бинарное отношение
В шаблонную формулу – ( (Оп-д1 Оп-д2)) Relation ( (Оп-д3 Оп-д4)) подставляют результаты, и получаю:
(a-b+2b)b*a/3^2
Построение графика
По данному отношению строю график:
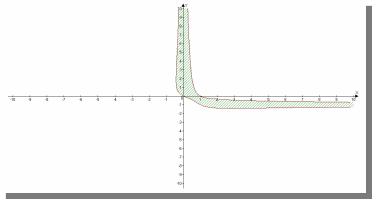
Исследование свойств отношения
Свойства отношений доказываются путём приведения примеров на графике:
Не функционален, так как содержит пары с одинаковыми первыми коэффициентами.
не инъективен, так как содержит пары с одинаковыми вторыми компонентами «b» и разными первыми компонентами «a».
Всюду определён, так как область определения не совпадает с областью отправления
Не сюрьективен так как его область значений не равна области прибытия.
Не биективен, так как не функционален, не инъективен и не сюрьективен.
Не рефлексивен так как график не содержит прямую в = а.
Анти рефлексивен так как график содержит точки , лежащие на прямых и = а.
Не иррефлексивен, так как найдутся точки, принадлежащие графику и лежащие на прямой в = а .
Не симметричен, так как найдутся точки, не принадлежащие графику и симметричные относительно прямой в = а.
Не анттисимметричен, так как найдутся точки, принадлежащие графику и не симметричные относительно прямой в = а.
Не транзитивен.
Свойства отношения внесены в таблицу:
Функциональность |
+ |
Инъективность |
+ |
Всюду определенность |
– |
Сюръективность |
+ |
Биективность |
+ |
Рефлексивность |
– |
Не рефлексивность |
– |
Антирефлексивность |
+ |
Симметричность |
– |
Асимметричность |
– |
Антисимметричность |
– |
Транзитивность |
– |

Задание №3 Минимизация пополненной функции с помощью карт
3.1. Пересечение объединений
|
|

К0= 0010 0111 0110 1111 1001 1010 1101
|
Ќ0= 0010 v 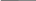
1010 v 0110 v 1001 v 1101 v 0111 v 1111 v
|
Ќ1= ~010 0~10 011~ 1~01 ~111
|
|||||||
Ќ1=
|
|||||||||
|
0010 |
1010 |
0110 |
1001 |
1101 |
0111 |
1111 |
||
~010 |
|
v |
|
|
|
|
|
||
0~10 |
v |
|
v |
|
|
|
|
||
011~ |
|
|
v |
|
|
v |
|
||
1~01 |
|
|
|
v |
|
|
|
||
~111 |
|
|
|
|
|
v |
v |
||
|
0010 |
0110 |
0111 |
|
0~10 |
v |
v |
|
A/3 |
011~ |
|
v |
v |
B/5 |
|
A |
A+B |
B |
|
0~10 1~01 ~111
|
ДНФ
=
|
Выводы
В ходе выполнения расчетно-графической работы по дисциплине «Основы дискретной математики» были закреплены основные теоретические знания и практические навыки.
В процессе расчетно-графической работы для построенных в соответствии с индивидуальным вариантом множественной формулы, бинарного отношения и логической схемы выполнен анализ, минимизация множественных и булевых формул, перевод булевых формул в заданный базис и синтез схем в заданном базисе.


 ~
~




 v
v
 Ядро:
~010
Ядро:
~010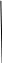 КНФ
=
КНФ
=
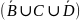
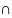

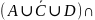 (
(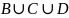 )
)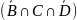
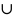
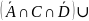
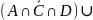 (
(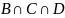 )
)