14. Гипотеза Бернулли.

Гипотеза Бернулли о плоских сечениях — поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

Гипотеза плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации. Ее называют еще гипотезой Бернулли. Эту гипотезу можно рассматривать как экспериментальный факт, наблюдаемый, например, при нанесении прямоугольной сетки на резиновый стержень. При изгибе такого стержня продольные линии ис­кривляются, в то время, как поперечные линии остаются прямыми. Эта гипотеза относится только к длинным и тонким стержням и используется при выводе большинства формул для расчета брусьев.

14. Центральное растяжение-сжатие. Внутренние силы в поперечном сечении бруса. Анализ формулы для вычисления напряжений впоперечном сечении бруса.

Растяжение или сжатие стержня вызываются силами вдоль его оси. В этом случае в поперечном сечении возникает только внутренняя сила, а именно продольная – N. 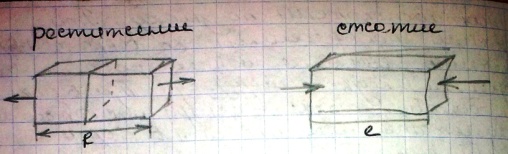Продольная сила N является равнодействующей силой упругости, рассчитывается через внешнюю нагрузку и численно равна проекции всех внешних сил расположенных по одну сторону от проведенного сечения. 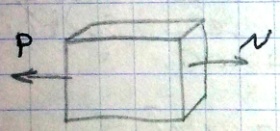Σ=0; => Σ=P-N=0; => N=P

14. Удлинение-укорочение бруса при центральном растяжении-сжатии.

Зак Растяжение-сжатие— вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс).Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила.

l - первоначальная длина стержня; Δl – абсолютное удлинение(абсолютное укорочение); ℰ= Δl/l – относительное удлинение(относительное укорочение)При упругой деформации зависимость между напряжением и относительной деформацией определяется законом Гука. , где Е – модуль продольной упру гости, некоторая физическая постоянная, которая характеризирует материал.

он Гука.

14. Коэффициент Пуасонна.

Коэффициент Пуассона – отношение деформации по незагруженному направлению к деформации по загруженному направлению. Характеризует упругие свойства материала. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5

, где μ — коэффициент Пуассона; = Δa/a — деформация в поперечном направлении (отрицательна при осевом растяжении, положительна при осевом сжатии);ε — продольная деформация (положительна при осевом растяжении, отрицательна при осевом сжатии).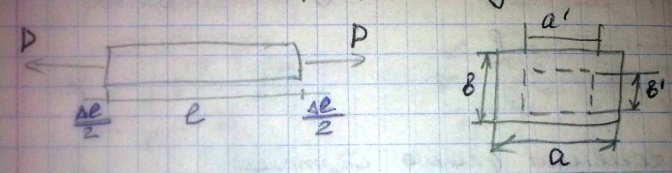

Δl – абсолютная продольная деформация(удлинение)

Δa=a-a ́ – абсолютная поперечная деформация.