
- •Вектори на прямій, на площині і в просторі. Базиси, системи координат.
- •Питання, що розгортатимуться в лекції:
- •Скалярний, векторний та мішаний добутки векторів.
- •Питання, що розглядатимуться в лекції.
- •Визначники другого та третього порядків.
- •Питання, що розгортатимуться в лекції:
- •Рівняння прямої лінії на площині.
- •Питання, що розглядатимуться в лекції.
- •Полярна система координат на площині. Питання, що розглядатимуться в лекції.
- •Лекції 7-8-9. Рівняння кривих другого порядку на площині.
- •Питання, що розглядатимуться в лекції.
- •Поворот координатних осей.
- •Загальний випадок.
- •Контрольні питання.
- •Арифметичні простори. Матриці лінійні простори
- •Питання, що розглядатимуться в лекції.
- •Арифметичні простори.
- •Лінійні операції в арифметичному просторі.
- •Матриці.
- •Добуток матриць.
- •Лінійні простори.
- •Приклади лінійних просторів.
- •Контрольні питання.
- •Вправи до виконання.
- •Лінійні підпростори. Лінійні оболонки Нові терміни:
- •Питання, що розглядатимуться в лекції.
- •Контрольні питання.
- •Вправи до виконання.
- •Питання, що розглядаються в лекції.
- •Ранг матриці.
- •Контрольні питання.
- •Вправи до виконання.
Контрольні питання.
Означення лінійного підпростору.
Навісти приклади лінійних підпросторів.
Означення лінійної комбінації векторів.
Означення тривіальної лінійної комбінації векторів.
Означення нетривіальної лінійної комбінації векторів.
Означення лінійно незалежної системи векторів.
Означення лінійно залежної системи векторів.
Означення лінійної оболонки системи векторів.
Означення повної в просторі системи векторів.
Чи витікає з лінійної незалежності системи векторів її повнота в просторі?
Чи обов'язкова вимога лінійної незалежності для повноти системи?
Привести приклади повних лінійних просторах систем.
Чи буде система поліномів f1(x) = 1, f2(x) = x, f3(x) = x2, f4(x) = x3 повною в
 ?
?Чи буде система
 ,
,
 ,
,
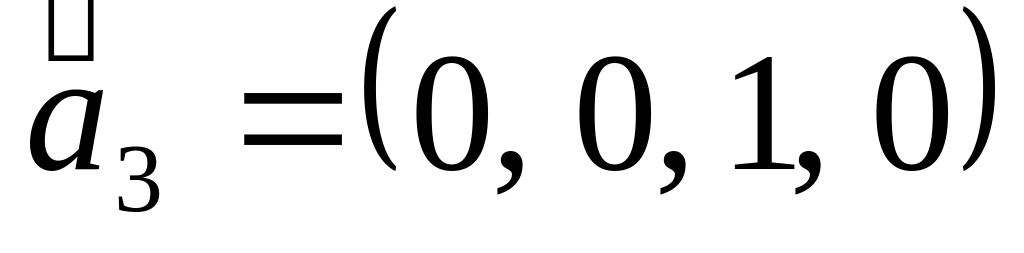 ,
,
 повною в R4?
повною в R4?Чи буде система матриць
А1 = , А2 = , А3 = , А4 =
лінійно залежною?
Чи будуть лінійно залежними два неколінеарних вектори в E2 чи E3?
Чи будуть лінійно залежними три некомпланарних вектори?
Як виглядає лінійна комбінація векторів
 з Rn?
з Rn?Привести приклад лінійно незалежної системи поліномів .
Привести приклад системи лінійно незалежних матриць в M33.
Вправи до виконання.
Довести, що £1 =
 Rn
:
Rn
:
 є лінійний підпростір Rn.
є лінійний підпростір Rn.Довести, що £1 =
 Rn
:
Rn
:
 є лінійний підпростір Rn.
є лінійний підпростір Rn.Довести, що £1 = Rn :
 є лінійний підпростір
Rn.
є лінійний підпростір
Rn.Довести, що £1 = Rn :
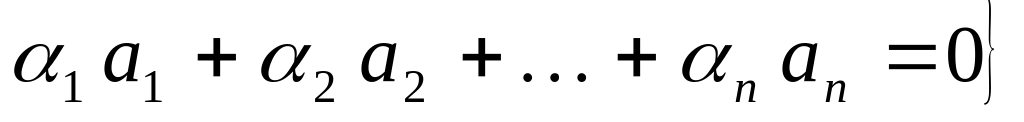 є лінійний підпростір Rn.
є лінійний підпростір Rn.Довести, що £1 = Rn :
 є лінійний підпростір Rn.
є лінійний підпростір Rn.Довести, що
£1 =

є лінійний підпростір Mmm.
Довести, що £1 =
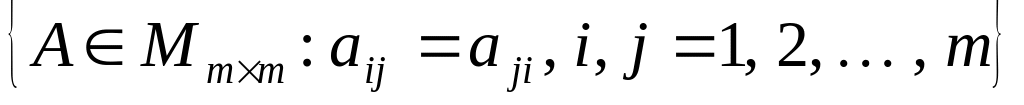 – множина симетричних матриць – є
лінійний підпростір Mmm.
– множина симетричних матриць – є
лінійний підпростір Mmm.Довести, що £1 =
 – множина косометричних матриць – є
лінійний підпростір Mmm.
– множина косометричних матриць – є
лінійний підпростір Mmm.Довести, що £1 =
 є лінійний підпростір Mmn.
є лінійний підпростір Mmn.Довести, що
£1 =

є лінійний підпростір Mmn.
Довести, що система поліномів f1(x) = x – 1, f2(x) = x + 1, f3(x) = x2, – лінійно незалежна.
Перевірити, чи буде лінійно незалежною система векторів
 ,
,
 ,
,
 .
.Довести, що система матриць
А1 =
![]() ,
А2 =
,
А2 =
![]() ,
А3 =
,
А4 =
,
А3 =
,
А4 =
лінійно незалежна.
Довести, що система векторів a1 + a2, a1 – a2, a1 + a2 + a3, лінійно незалежна, якщо система a1, a2, a3 лінійно незалежна.
Довести, що система векторів a, 2a, b, c – лінійно залежна.
Довести, що система поліномів
![]()
повна у .
Довести, що система матриць
А1 = , А2 = , А3 = , А4 =
повна у
![]() .
.
Довести, що система векторів
 ,
,  , ...
,
, ...
, 
лінійно незалежна і повна у Rn.
Довести, що кожна підсистема лінійно незалежної системи векторів лінійно незалежна.
Довести, що якщо до повної лінійно незалежної системи додати декілька векторів, вона залишиться лінійно незалежною.
Довести, що у лінійно залежної системи може бути підсистема.
Знайти лінійну оболонку матриць

Знайти лінійну оболонку поліномів f1(x) = x – 1, f2(x) = x + 1.
Знайти лінійну оболонку векторів
![]() Т,
Т, ![]() Т,
Т, ![]() Т.
Т.
ЛЕКЦІЯ 12-13.
ЛІНІЙНІ ВІДОБРАЖЕННЯ ЛІНІЙНИХ ПРОСТОРІВ.
ЕКВІВАЛЕНТНІ СИСТЕМИ.
БАЗИСИ І ВИМІРНІСТЬ ЛІНІЙНИХ ПРОСТОРІВ.
РАНГ МАТРИЦІ ТА ЙОГО ОБЧИСЛЕННЯ.
Нові терміни:
лінійна залежність |
- линейная зависимость |
- linear dependence |
еквівалентні системи |
- эквивалентные системы |
- equivalent systems |
максимальна лінійно незалежна система |
- максимальная линейно независимая система |
- maximal linear independent system |
база системи |
- база системы |
- base of systems |
ранг системи |
- ранг системы |
- rang of system |
базис лінійного простору |
- базис линейного пространства |
- base of linear space |
вимірність |
- размерность |
- dimension |
ранг матриці |
- ранг матрицы |
- rang of matrix |
елементарні перетворення |
- элементарные преобразования |
- elementary transformation |
