
9. Економетричні моделі динаміки
9.1. Ряди динаміки
Досліджуючи перебіг певного процесу чи явища в часі виділяють умовно такі його складові:
Тренд, який відображає вплив причинно-наслідкових закономірностей, властивих досліджуваному процесу і обумовлених довготривалими факторами (наприклад, збільшення чисельності населення, вплив НТП);
Сезонна компонента, обумовлена можливими повтореннями впливу деяких тимчасових факторів протягом відносно короткого терміну часу – кварталу, місяця (наприклад, сезонний попит на товари);
Циклічна компонента, з використанням якої намагаються врахувати можливі періодично повторювані умови змін в перебігу досліджуваного процесу
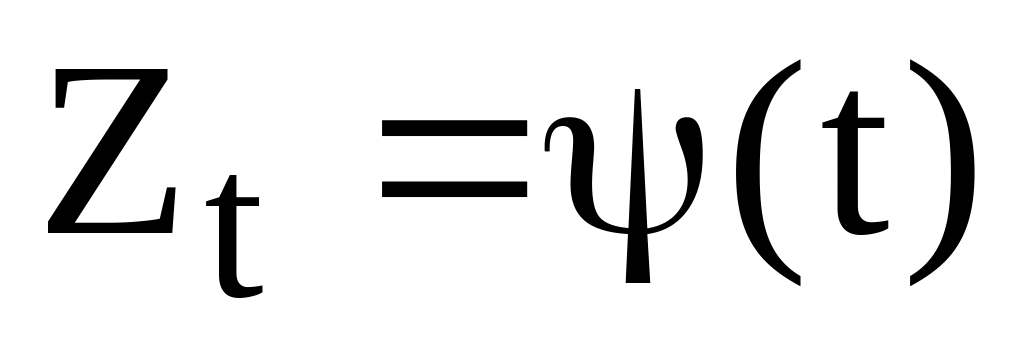 ;
;Випадкова компонента, за допомогою якої враховують вплив випадкових непередбачених факторів
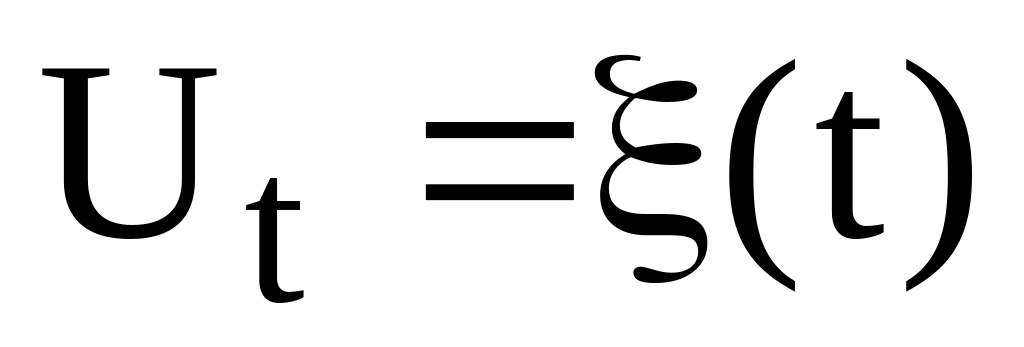 .
.
У більшості випадків фактичний рівень часового ряду наводиться як сума або добуток трендової, сезонної, циклічної та випадкової компонентів:
![]() - адитивна
модель;
- адитивна
модель;
![]() - мультиплікативна
модель.
- мультиплікативна
модель.
Через неможливість або істотні труднощі в одночасному дослідженні всіх чотирьох компонент виділяють дві складові:
невипадкову;
випадкову.
Невипадкова складова об’єднує тренд, сезонну компоненту та циклічну компоненту. В літературі невипадкова складова часто фігурує під назвою «тренд».
Побудову трендової моделі застосовують в тих випадках, коли фактори є сталі за часом та не передбачається швидких змін на ринку. При цьому вважається, що ці дані виражають постійні причинно-наслідкові зв’язки, які можна виявити завдяки статистичному аналізу.
Для проведення статистичного аналізу ряд динаміки розглядають як числову послідовність спостережень, які характеризують економічний процес чи явище в часі. Динамічний ряд складається з двох елементів:
рівнів ряду (статистичних показників);
моментів часу, до яких ці рівні стосуються.
За тенденціями зміни досліджуваний показник може бути представлений аналітичною залежністю в координатах «час – показник» і відповідає певній лінії, яку називають траєкторією.
Аналітична залежність досліджуваного показника від часу та його траєкторія показують наслідки впливу основних закономірностей на перебіг процесу, які до певної міри позбавленні впливу випадкових факторів. Тому приймають, що відхилення експериментальних даних від відповідних аналітичних обумовлене впливом випадкових причин.
Таким чином рівні y(t) часового ряду можна подати у вигляді залежності:
![]() ,
(9.1)
,
(9.1)
де f(t) – аналітичне представлення тренда із врахуванням можливих сезонних і циклічних складових u(t) – це відхилення експериментальних даних від аналітичних які обумовленні впливом випадкових факторів.

Рис.9.1 Тренд
9.2. Аналітичне вирівнювання динамічного ряду
Рівні економічних часових рядів коливаються, тому тенденція розвитку у часі не може бути визначена через випадкові відхилення рівнів у той чи інший бік. Щоб чітко визначити основну тенденцію ряду (тренд) для подальшого прогнозування використовуючи певну трендову модель, розроблені методи згладжування (вирівнювання) часових рядів.
Методи згладжування часових рядів поділяють на дві групи:
методи механічного згладжування ряду;
аналітичне вирівнювання, яке базується на кривих зростання.
Найпростішим механічного згладжування є метод плинної середньої.
Плинною середньою називають середню величину рівнів ряду для кількох послідовних проміжків початкового ряду. Використання плинних середніх дозволяє певною мірою уникнути наслідків впливу випадкових величин.
Метод плинної середньої ґрунтується на ідеї обчислення середньої величини для певного проміжку. Новий ряд рівні якого є усередненими значеннями рівнів початкового ряду має менші відхилення від значень досліджуваного показника.
Обчислена середня ставиться у відповідність середині проміжку. Оскільки проміжок може мати парну або не парну кількість точок, то методика обчислення середньої трохи змінюється. За умови усереднення не парної кількість точок 2р+1 середня величина ставиться у відповідність центральній точці.
Якщо точки проміжків умовно пронумерувати від 1 до 2р+1, то формула для обчислення середньої буде мати вигляд:
![]() (9.2)
(9.2)
За наведених умов по завершенні операції усереднення отриманий ряд буде мати на 2р елементів менше ніж початковий.
Недоліками цього методу є:
перші та остатні р рівнів не згладжуються;
його можна використовувати для рядів, які мають лінійну тенденцію.
Це одним методом вирівнювання динамічного ряду є метод експотенційтого згладжування. Його особливість полягає в тому що, при знаходженні згладжуваного рівня використовується значення лише попередніх рівнів ряду, які беруться з певною вагою. Вага рівня ряду зменшується залежно від того наскільки віддалений рівень від моменту часу для якого визначається згладжуване значення.
Якщо для часового ряду у1,у2,у3,....,yn відповідні згладження значень позначимо через S1,S2,S3,….,Sn, то експотенційне згладжування розраховуватиметься за формулою:
![]() (9.3)
(9.3)
де α – це параметр для згладжування, 0<α<1
Тобто St є зваженою середньою всіх попередніх рівнів.
Для St-1 отримаємо
![]()
У практичних
задачах α рекомендується вибирати з
проміжку [0,1;0,3], а
![]() або
або
![]() .
.
Приклад
Використовуючи метод плинних середніх, провести згладжування за трирівневим інтервалом та експотенційне згладжування (α =0,2, ).
Періоди |
Обсяг випуску тис.шт. |
Згладжування ряду за трирівневим інтервалом |
Експотенційне згладжування |
1 |
30 |
- |
30,00 |
2 |
31 |
30,67 |
30,20 |
3 |
31 |
31,33 |
30,36 |
4 |
32 |
31 |
30,69 |
5 |
30 |
30,67 |
30,55 |
6 |
30 |
30,67 |
30,44 |
7 |
32 |
31 |
30,75 |
8 |
31 |
32 |
30,80 |
9 |
33 |
31,67 |
31,24 |
10 |
31 |
31,67 |
31,19 |
11 |
31 |
31,67 |
31,15 |
12 |
33 |
32 |
31,52 |
13 |
32 |
32,67 |
31,62 |
14 |
33 |
33 |
31,90 |
15 |
34 |
- |
32,32 |
Аналітичне вирівнювання динамічного ряду здійснюється за допомогою кривих зростання.
Щоб правильно підібрати найкращу криву зростання для моделювання економічного явища необхідно знати особливості кожного виду кривих. Найчастіше використовується:
Поліноміальні прямі:
 поліном першого
степеня
поліном першого
степеня поліном другого
степеня
поліном другого
степеня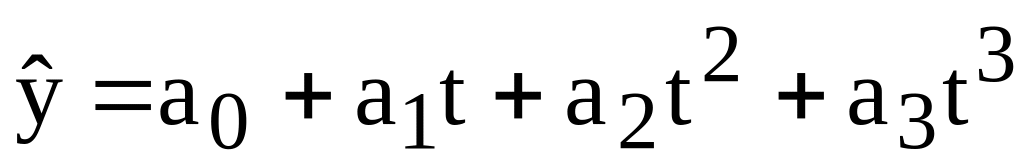 поліном третього
степеня
поліном третього
степеня
....................................
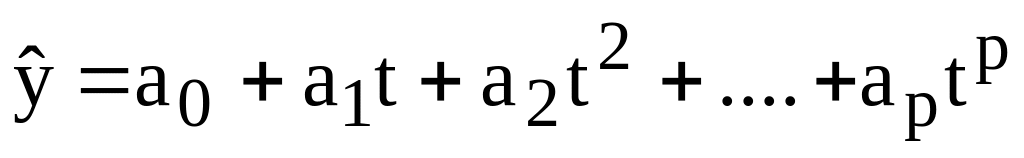 поліном степеня
р
поліном степеня
р
Гіперболічна функція
