12

7. Лінійні моделі множинної регресії

7.1. Класична лінійна багатофакторна модель, основні етапи її побудови

На практиці економічні явища змінюються під впливом багатьох факторів, які треба вміти виявити і оцінити. Наприклад, на обсяг продажу впливає ціна, якість товару, рівень доходів населення, сплати споживачів, наявність взаємозалежних і доповнюючих товарів, рекламні заходи тощо.

Багатофакторний регресійний аналіз допомагає знайти явний вигляд такої залежності та кількісно оцінити вплив різних факторів на економічний процес.

В загальному вигляді багатофакторна лінійна регресія матиме вигляд:

(7.1)

де - параметри моделі;

- фактори (незалежні змінні);

У – показник (залежна змінна);

u – випадкові величини (відхилення).

Процес побудови багатофакторної моделі складається з декількох етапів:

1. вибір та аналіз усіх можливих факторів, які впливають на процес (або показник), що вивчається;

2. вимірювання та аналіз визначених факторів;

3. вибір методу та побудова регресійної багатофакторної моделі;

4. оцінка невідомих параметрів;

5. перевірка моделі на адекватність;

6. розрахунок основних характеристик та побудова інтервалів довіри;

7. аналіз отриманих результатів та висновки.

7.2. Розрахунок параметрів багатофакторної регресії за методом найменших квадратів

Введемо припущення щодо відхилень u_i:

1. для кожного спостереження і=1,n u_i - випадкова величина;

2. , відхилення u_i мають однакову дисперсію;

3. , математичне сподівання відхилень дорівнює 0;

4. u_i та u_j не корельовані при .

Оцінку параметрів знайдемо за допомогою МНК:

(7.2)

Згідно з необхідною умовою екстремуму функції багатьох змінних у точках екстремуму частинні похідні дорівнюють нулю. Знаходячи частинні похідні та прирівнюючи їх до нуля, отримаємо

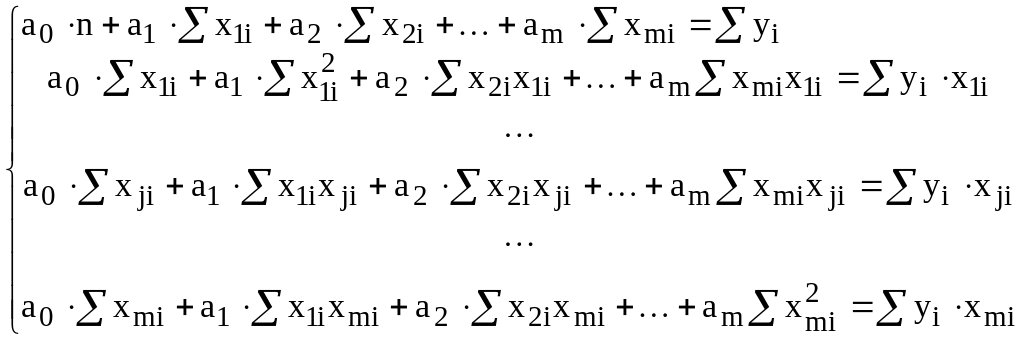(7.3)

Розв'язавши таку систему, отримаємо оцінки параметрів .

7.3. Матричний вигляд багатофакторної регресії

У результаті спостережень за об’єктом за n періодів (років, кварталів, місяців) або спостережень за один період над n об’єктами в яких показник залежить від m факторів, отримані такі дані:

Таблиця 7.1

Статистичні дані

у	х1	х2	...	хj	...	xm
y1	x11	x21	…	xj1	…	xm1
y2	x12	y22	…	xj2	…	xm2
…	…	…	…	…	…	…
yi	x1i	x2i	…	xji	…	xmi
…	…	…	…	…	…	…
yn	x1n	x2n	…	xjn	…	xmn

Припустимо, що між показником у і факторами x₁,х₂,...,x_m існує лінійна залежність у вигляді (7.1):

Для n дослідів можна скласти n рівнянь виду:

…

Ці рівняння можна записати у матричній формі:

(7.4)

де вектор спостережуваних даних показника.

- матриця спостережуваних значень факторів х_і, і=1, m, х₀ – фіктивний фактор, всі значення якого дорівнюють 1

- вектор оцінюваних параметрів

- вектор відхилень фактичних даних від розрахункових.

Визначити значення параметрів можна за формулою:

(7.5)

Під час практичного розв’язання цієї задачі розрахунки необхідно проводити в такому порядку:

1. Знайти добуток матриць Х^TХ.

2. Знайти обернену матрицю [Х^TХ]^–1.

3. Знайти добуток матриці Х^T на вектор .

4. Знайти добуток матриці [Х^TХ]^–1 на вектор .

В результаті отримаємо вектор оцінок параметрів .