
4. Решение систем нелинейных уравнений
Метод Ньютона
Для системы второго порядка
f(x,y) = 0,
g(x,y) = 0.
Последовательные приближения по методу Ньютона вычисляются по формулам
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Метод Ньютона сходится, если начальное приближение выбрано удачно и матрица Якоби невырожденная, причем сходимость квадратичная. На практике итерации обычно заканчивают, когда одновременно достаточно малы значения |f(xn,yn)| и |g(xn,yn)| или разности |xn+1–xn| и |yn+1–yn|. Для выбора начального приближения применяют графический метод, метод проб и т.д.
Пример. Решить систему уравнений
![]()
Решение в системе Maple:
1) Очистим оперативную память. Нам в дальнейшем потребуется функции det и implicitplot, которых нет в ядре системы, поэтому здесь подключим пакет линейной алгебры linalg и графических построений plots.
> restart;
> with(linalg): with(plots):
2) Зададим функции f(x,y) и g(x,y).
> f:=(x,y)->x^7-5*x^2*y^4+1510;
> g:=(x,y)->y^5-3*x^4*y-105;
3) Для отделения корней системы построим графики неявных функций f(x,y)=0 и g(x,y)=0.
> implicitplot({f(x,y)=0,g(x,y)=0},x=-5..5,y=-5..5);
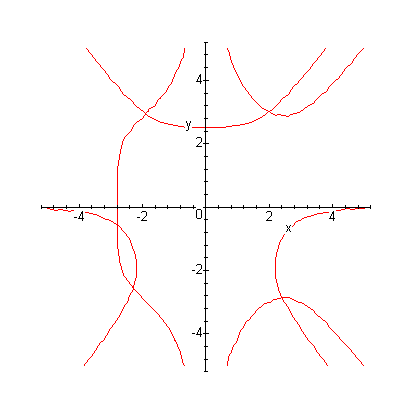
Видим пять пересечений графиков, значит, система имеет (минимум) пять корней.
4) Определим якобиан
> J:=[[diff(f(x,y),x),diff(f(x,y),y)],[diff(g(x,y),x),diff(g(x,y),y)]];
5) Введём функцию Jn(x,y), являющуюся определителем матрицы J.
> Jn:=unapply(det(J),x,y);
6) Определим величины An и Bn в виде соответствующих определителей
> An:=det([[f(x,y),diff(f(x,y),y)],[g(x,y),diff(g(x,y),y)]]);
> Bn:=det([[diff(f(x,y),x),f(x,y)],[diff(g(x,y),x),g(x,y)]]);
7) Присвоим начальные значения переменным. x0 и y0 определяет точку начального приближения (определяется графически).
> x0:=-3; y0:=-1.; eps:=0.001: n:=0:
8) Организуем цикл вычислений по методу Ньютона
> while abs(f(x0,y0))+abs(g(x0,y0))>eps do
> if abs(Jn(x0,y0))<10^(-4) then print(`Якобиан = 0`); break fi;
> x0:=x0-subs(x=x0,y=y0,An)/Jn(x0,y0);
> y0:=y0-subs(x=x0,y=y0,Bn)/Jn(x0,y0);
> if n=50 then break fi;
> n:=n+1;
> od:
9) Вывод результата: (x0,y0) – решение системы, n – число итераций
> evalf({x0,y0});n;
10) Для вычисления остальных четырёх корней системы нужно выполнить шаги 7)–9), предварительно изменив в п. 7) начальные приближения соответственно на
> x0:=-3; y0:=-3.;
> x0:=2; y0:=-3.;
> x0:=-2; y0:=3.;
> x0:=2; y0:=3.;
5. Использование стандартных функций системы Maple
Maple имеет мощные средства для решения линейных и нелинейных уравнений. Для аналитического решения используется достаточно универсальная и гибкая функция solve. solve(eqn, var);
solve({eqn1,eqn2,…}, {var1,var2,…});
Здесь eqn, eqn1, … – уравнения, содержащие неизвестные переменные var, var1, …
Используя функцию solve в комбинации с функциями evalf или convert, можно получить корни в численном виде. Если результат представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции allvalues.
Для получения численного решения нелинейного уравнения или системы уравнений удобно использовать функцию
fsolve(eqns,vars,options);
Эта функция может быть использована со следующими параметрами:
complex – находит один или все корни (чаще полинома) в комплексной форме
fulldigits – определяет счет для полного числа цифр, заданного функцией Digits
maxsols=n – задает вычисление только n корней
interval – задается в виде a..b или x=a..b, или { x=a..b, y=c..d, … } и обеспечивает поиск корней в указанном интервале.
Для вычисления корней полиномов, зависящих от одной переменной, существует специальная функция roots. В простейшем варианте roots(a) (или roots(a,x) ) она возвращает рациональные корни полинома a с указанием их кратностей.
Примеры.
> solve(x^3-2*x+1,x);
![]()
> eq:= x^4-5*x^2+6*x=2:
> sols:= [solve(eq,x)];
sols := [–1+![]() ,
–1–
,
1, 1]
,
–1–
,
1, 1]
> sols[1];
–1+
> evalf(sols);
[.732050808, –2.732050808, 1., 1.]
> solve(sqrt(ln(x))=2,x);
e4
> evalf(");
54.59815003
> solve(x^5-3*x^4+2*x^2-x+3,x);
RootOf(_Z5 – 3 _Z4 + 2 _Z2 – _Z + 3)
> allvalues(");
–1.127479307, .03687403922 – .8565945569 I,
.03687403922 + .8565945569 I, 1.327862375, 2.725868853
> solve({exp(x)=sin(x)},x);
{x = RootOf(_Z – ln(sin(_Z)))}
> allvalues(");
{x = .3627020561 – 1.133745919 I}
> fsolve(exp(x)=sin(x),x=–4..0);
–3.183063012
> fsolve(exp(x)=sin(x),x=–7..–4);
–6.281314366
> fsolve(exp(x)=sin(x),x,complex);
.3627020561 – 1.133745919 I
> solve( {x^2*y^2=0, x-y=1} );
{y = –1, x = 0}, {y = –1, x = 0}, {x = 1, y = 0}, {x = 1, y = 0}
> f:=x^7-5*x^2*y^4+1510:
> g:=y^5-3*x^4*y-105:
> s1:=solve({f,g},{x,y}); #Результат этой функции не приводится
> evalf(");
{x = –2.844483289, y = –.5348543088}
> allvalues(s1); # Ниже приводится только часть результата
{x = –2.844483289, y = –.5348543088}, {y = –2.573256586, x = –2.304767679},
{y = .1857181696+2.786617077 I, x = –2.107398990–.1931448896 I}
{x = –2.107398990+.1931448896 I, y = .1857181696–2.786617077 I},
{y = 2.957183542, x = –1.922332687},
--------------------------------------------------------
{x = 15.00039270, y = 19.74216374}
> fsolve({sin(x+y)-exp(x)*y=0,x^2-y=2},{x,y},{x=-1..1,y=-2..0});
{x = –.6687012050, y = –1.552838698}
> roots(2*x^3+11*x^2+12*x-9);
[[–3, 2], [![]() ,
1]]
,
1]]
