1.3.2. Стратегии поиска в пространстве состояний

Чтобы применять алгоритмы поиска, разработчик должен уметь анализировать и прогнозировать их поведение и знать, гарантировано ли нахождения решения в результате поиска, является ли поиск конечным, или возможны зацикливания, зависит ли процесс поиска от времени выполнения и используемой памяти, каким образом интерпретатор может упростить поиск, и как вообще разработать интерпретатор. На эти вопросы даст ответ теория поиска, которая выходит за пределы этой книги. Представив пространство состояний задачи в виде графа, необходимо найти ее решение. Решение находится в результате поиска. Порядок, в котором происходит развертывание состояний, определяется стратегией поиска. Можно использовать теорию графов для анализа процедуры поиска. Поиск в пространстве состояний можно вести в двух направлениях: от исходных данных задачи (фактов) к цели и в обратном направлении от цели к исходным данным (фактам). Прямой поиск идет от исходного состояния, когда целевое состояние задано неявно, обратный - от целевого состояния, когда исходное состояние задано неявно, а целевое явно.

При прямом поиске (поиске на основе данных) исследователь начинает процесс решения задачи, анализируя ее условие, а затем применяет правила к известным фактам для получения новых фактов, которые, в свою очередь, используются для генерации новых фактов, и т. д. Этот процесс продолжается до тех пор, пока не повезет, и не будет достигнуто целевое состояние. При обратном поиске вначале выдвигают цель, а затем возвращаются назад к фактам, пытаясь найти те, которые подтверждают эту цель. Если цель оказалась правильной, то выбирается следующая цель, которая детализирует первую и является по отношению к ней подцелью. Далее отыскиваются факты, подтверждающие истинность подчиненной цели. Поиск продолжается от подцелей, пока не будут достигнуты исходные данные задачи. Такую стратегию поиска называют управляемой целями.

Выбор стратегии зависит от структуры решаемой задачи. Процесс поиска от цели рекомендуется применять в тех случаях, когда цель поиска присутствует в постановке задачи. Поиск на основе данных применим к решению задач, в которых данные определены в постановке задачи и когда сформулировать цель очень трудно. В системах диагностики чаще применяется прямой поиск, в то время как в планирующих системах более эффективным оказывается обратный поиск.

Двунаправленный поиск осуществляется одновременно из исходного состояния и множества целевых состояний. Двунаправленный поиск заканчивается тогда, когда (и если) два фронта поиска встречаются. Такой поиск имеет преимущество перед однонаправленным поиском и требует решения двух проблем: смены направления поиска и оптимизации «точки встречи», так как прямой и обратный пути могут разойтись.

Определив направление поиска (от данных или цели), алгоритм поиска должен определить порядок исследования состояний дерева или графа. Рассмотрим две возможных стратегии последовательности обхода узлов графа: поиск в глубину (вглубь) и поиск в ширину (вширь) (рис. 1.2.).

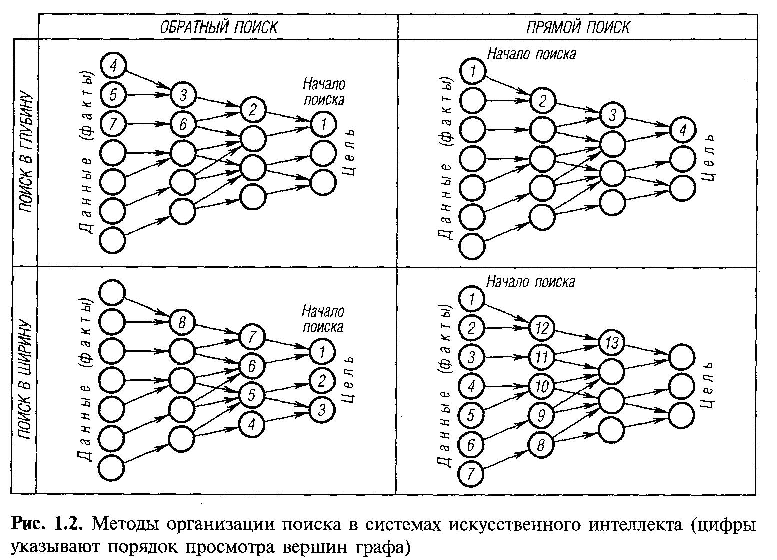
Рисунок 1.2. Методы организации поиска в системах искусственного интеллекта

При поиске в глубину в качестве очередной подцели выбирается та, которая соответствует следующему, более детальному уровню описания задачи. То есть, после исследования факта сначала необходимо оценить всех его потомков и их потомков, а затем исследовать любую из вершин-братьев. Если дальнейшие потомки фактов не найдены, рассматриваются вершины-братья.

При поиске в ширину система вначале анализирует все факты, находящиеся на одном уровне пространства состояний, и лишь потом переходит к фактам следующего уровня детализации.

Эвристический поиск осуществляется с помощью совокупности правил для выбора тех ветвей из пространства состояний, которые с наибольшей вероятностью приведут к приемлемому решению проблемы. Эвристика — это только предложение следующего шага, который будет сделан на пути решения проблемы. Эвристические алгоритмы состоят из двух частей: эвристической меры и алгоритма, который использует ее для поиска в пространстве состояний. Одним из самых распространенных эвристических алгоритмов поиска является процедура поиска экстремума. Стратегии, основанные на поиске экстремума, оценивают не только текущее состояние поиска, но и его потомков. Для дальнейшего поиска выбирается наилучший потомок, при этом о его братьях и родителях просто забывают. Поиск прекращается, когда достигается состояние, которое лучше, чем любой из его наследников. В локальном максимуме стратегия поиска экстремума останавливается. Этот факт является ее основным недостатком, поэтому такой алгоритм иногда бывает неприемлем для решения задачи. Однако этот алгоритм может быть очень эффективным, если оценивающая функция позволяет избежать локального максимума и зацикливания алгоритма.

«Жадный» алгоритм использует более гибкий метод поиска, при котором возможно использование приоритетной очереди для восстановления алгоритма из точки локального максимума.

Стратегия разбиения на подзадачи подразумевает выделение подзадач, решение которых рассматривается как достижение промежуточных целей на пути к конечной цели. Если удается правильно понять сущность задачи и оптимально разбить ее на систему иерархически связанных целей-подцелей, то можно добиться того, что путь к решению задачи в пространстве поиска будет минимален.

При стратегии разбиения на подзадачи часто в ИИ используются деревья. Они используются для моделирования ходов в играх, когда нельзя применить алгоритм поиска в пространстве состояний. Дерево игры моделирует игру двух лиц с нулевой суммой и с полной информацией. Для таких игр разумной считается стратегия минимакса, минимизирующая при выборе хода максимальные потери от следующего хода противника при просмотре на п шагов вперед.

Альфа-бета процедура применяется для уменьшения пространства состояний путем удаления из него ветвей, неперспективных для поиска успешного решения. При этом просматриваются только те вершины, в которые можно попасть в результате следующего шага, после чего неперспективные направления исключаются. Данная стратегия является определенным компромиссом между поиском в ширину и поиском в глубину. Для ее успешной реализации необходимо располагать дополнительными эвристическими знаниями, которые используются при выборе перспективных направлений. Эффективность и обоснованность этой процедуры зависят от выбора эвристической функции и от глубины просмотра вперед. Альфа-бета алгоритм нашел широкое применение в основном в системах, ориентированных на различные игры, и в шахматных задачах.

Вопросы

1.5. Назовите основные направления исследований, проводимые в области ИИ, охарактеризуйте их.

1.6. Как вы понимаете термин «пространство состояний»? Как оно выглядит при игре в шашки?

1.7. Как организовать прямой и обратный поиск в глубину?

1.8. Как организовать прямой и обратный поиск в ширину?

1.9. Графовое представление пространства состояний, как оно выглядит, его преимущества и недостатки.

1.10. Как выглядит пространство состояний при игре в «крестики-нолики» (5x5)?

1.11. Какие методы решения задач в теории и практике ИИ применяются, перечислите их и охарактеризуйте каждый из них.

1.12. Рассмотрим 8 фишек, которые могут перемещаться на поле из 9 клеток. Одна клетка остается пустой, так что фишки можно двигать и получать их различные конфигурации. Цель игры — найти такую последовательность перемещений фишек в пустую клетку, которая привела бы к заранее заданной целевой конфигурации. Постройте пространство состояний в этом случае.

1.13. Постройте некоторые состояния пространства состояний для игры в «пятнашки». Пятнадцать перенумерованных фишек размещены на поле из 16 клеток. Цель игры такая же — найти такую последовательность перемещений фишек в пустую клетку, которая привела бы к заранее заданной целевой конфигурации.