1.3. Решение задач и искусственный интеллект
Теория решения задач — важная часть ИИ. Предполагается существование счетного множества S (состояний) и множества O (операторов). При представлении задач в пространстве состояний решение задачи рассматривается как передвижение в пространстве состояний с целью достигнуть желаемого множества целевых состояний с помощью последовательности операторов. Задача решена, если найдена такая последовательность операторов
,
что
Где
- некоторое состояние из множества
начальных состояний;
-
некоторое
состояние из множества целевых состояний.
Важным этапом построения какого-либо описания задачи с использованием пространства состояний является выбор некоторой конкретной формы описания состояний этой задачи. В сущности, любая структура данных может быть использована для описания состояний. Это могут быть строки символов, векторы, двумерные массивы, деревья и списки. Как правило, выбираемая форма описания имеет сходство с некоторым физическим свойством решаемой задачи. Так, в игре в пятнадцать естественной формой описания состояний может быть массив 4x4. Выбирая форму описания состояний, нужно позаботиться и о том, чтобы применение оператора, преобразующего одно описание в другое, оказалось бы достаточно легким.
1.3.1. Графовое представление задачи в пространстве состояний.
Во многих задачах искусственного интеллекта часто возникает необходимость наглядного представления отношений между какими-либо объектами. Для таких отношений существует естественная модель — это ориентированный и неориентированный графы.
Ориентированный
граф (или
сокращено орграф)
G
=
(N,
E)
состоит
из множества
вершин N
и
множества дуг Е.
Вершины также называют узлами, а
дуги — ориентированными ребрами.
Множество вершин
,
,
…,
не обязано быть конечным. Дуга
представляется в виде упорядоченной
пары вершин
,
где
называется
началом, а
-
концом дуги. Дугу
часто
записывают как
.
Говорят так же, что дуга
ведет
от вершины
к вершине
,
а вершина
смежна с вершиной
.
Если
направленная дуга соединяет вершины
и
,
то
называется родителем
,
а
- потомком
.
Если граф содержит также дугу
,
то
и
называются
вершинами-братьями.
Корневой граф
имеет
единственную вершину
в которую не входит ни одна дуга. Таким
образом, корень графа не имеет родителей.
Концевая вершина — это вершина, которая не имеет потомков.
Упорядоченная
последовательность вершин
,
где каждая пара является дугой, называется
путем
длины п -1
на графе. Одну вершину можно считать
путем длины 0 от вершины к этой же вершине.
Путь называется простым, если все вершины
на нем, за исключением может быть первой
и последней, различны. Цикл — это простой
путь длины не менее 1, который начинается
и заканчивается в одной и той же вершине.
Если путь включает некоторую вершину более одного раза, то говорят, что путь содержит петлю.
Если к вершинам и дугам орграфа присоединить какую-либо информацию, то получим помеченный орграф, при этом каждая дуга и/или каждая вершина имеет соответствующие метки. Меткой может быть имя, вес или стоимость (дуги), или значение данных какого-либо заданного типа.
В корневом графе вершина называется предком всех вершин, расположенных после нее, и в то же время потомком всех вершин, расположенных на пути к ней.
Неориентированный
граф
состоит из конечного множества вершин
и
множества ребер
.
В отличие от ориентированного графа
каждое ребро здесь соответствует
неупорядоченной паре вершин если
-
неориентированное ребро, то
.
Неориентированный
граф будем называть просто графом.
Дерево
с базовым типом
в
программировании определяется как: 1)
пустое дерево; либо 2) некоторая вершина
типа
с
конечным числом связанных с ней отдельных
деревьев с базовым типом
,
называемых
поддеревьями.
В системах искусственного интеллекта
понятие дерева часто связывают с понятием
графа.
Рассматривая дерево как неориентированный граф, можно сказать, что в нем существует единственный путь между любыми двумя вершинами (т. е. пути в дереве не содержат циклов). Каждая вершина в корневом дереве имеет единственного родителя. Две вершины называются связными, если существует путь, содержащий эти вершины.
Множество состояний, достижимых из данного начального состояния, полезно представлять в виде графа, вершины которого соответствуют этим состояниям. Вершины такого графа связаны между собой дугами, которые описывают переходы между состояниями. Эти переходы соответствуют логическим заключениям или допустимым ходам в игре.
Поиск
в пространстве состояний характеризует
решение задачи как процесс
нахождения пути решения (цепочки, ведущей
к решению задачи) от исходного состояния
к целевому. Пространство состояний
можно представить четверкой
со следующими обозначениями:
—
множество вершин графа или состояний
в процессе решения задачи;
—
множество дуг между вершинами,
соответствующих шагам в процессе
решения задачи;
—
непустое множество начальных состояний
задачи;
—
непустое множество, состоящее из целевых
состояний. Эти состояния
описываются одним из следующих способов:
1) измеряемыми свойствами состояний, встречающихся в процессе поиска;
2) свойствами путей, возникающих в процессе поиска, например, стоимостью перемещения по дугам пути.
Допустимый путь — это путь из вершины множества в вершину из множества . Путь является целью поиска. Он начинается от исходного состояния и продолжается до тех пор, пока не будет достигнуто условие цели.
Задача алгоритма поиска решения состоит в нахождении допустимого пути в пространстве состояний. Состояния иногда могут быть достигнуты разными путями, поэтому важно выбирать оптимальный путь.
Графовое представление задачи в пространстве состояний имеет ряд преимуществ:
● интуитивно легко понять нетривиальные высказывания;
●
учитывается
стоимость применения оператора
она
помечается на
каждой дуге графа;
● каждый последовательный шаг можно определять при помощи функции сравнения целевого и текущего состояний.
Приведем
фрагмент пространства состояний для
игры «крестики-нолики»
(рис. 1.1.). Корневая вершина этого графа
будет соответствовать пустой игровой
доске, указывающей на начало игры. Каждый
следующий узел графа будет представлять
состояние игровой доски, возникающее
в процессе
игры в результате допустимых ходов, а
дуги между ними -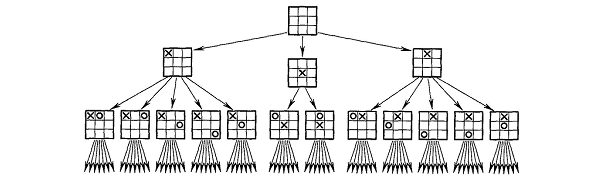
Рисунок 1.1. Фрагмент пространства состояний для игры в "крестики-нолики"
связи между вершинами. Представление в пространстве состояний позволяет рассматривать все возможные варианты игры как различные пути на графе пространства состояний. Описав игру таким образом, можно с помощью поиска на графе найти эффективную игровую стратегию, то есть определить все пути, которые ведут к наибольшему числу побед и наименьшему числу поражений, и выбрать игру, которая будет вынуждать противника идти по одному из оптимальных для нас путей. Вторым достоинством представления пространства состояний в виде графа является возможность реализации игры на компьютере.