5.2.2. Обучение искусственных нейронных сетей

Сеть обучается, чтобы для некоторого множества входов давать требуемое (или, по крайней мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор. Различают алгоритмы обучения с учителем и без учителя.

Обучение с учителем предполагает, что для каждого входного векто­ра существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной век­тор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть, и веса изменяются в соответствии с алгоритмом, стремящимся ми­нимизировать ошибку. Векторы обучающего множества предъявляются последовательно, для каждого вектора вычисляются ошибки и подстраи­ваются веса до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Обучение без учителя не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выде­ляет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения.

5.3. Теорема Колмогорова

Рассмотрим в качестве примера двухслойную нейронную сеть с n входами и одним выходом, которая достаточно проста по структуре и в то же время широко используется для решения прикладных задач. Эта сеть изображена на рис. 6.6. Каждый i-й нейрон первого слоя имеет n входов, которым приписаны веса

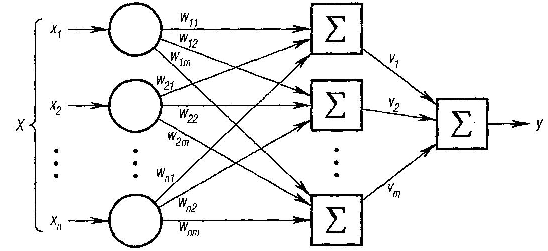
Рис. 6.6. Пример нейронной сети

Получив входные сигналы, нейрон суммирует их с соответствующи­ми весами, затем применяет к этой сумме передаточную функцию и пересылает результат на вход нейрона второго (выходного) слоя. В свою очередь, нейрон выходного слоя суммирует полученные от второго слоя сигналы с некоторыми весами Для определенности будем предпола­гать, что передаточные функции в скрытом слое являются сигмоидальными, а в выходном слое используется тождественная функция, т. е. взвешенная сумма выходов второго слоя и будет ответом сети.

Подавая на входы любые числа мы получим на выходе значение некоторой функции которое является отве­том (реакцией) сети. Очевидно, что ответ сети зависит как от входного сигнала, так и от значений ее внутренних параметров - весов нейронов. Выпишем точный вид этой функции:

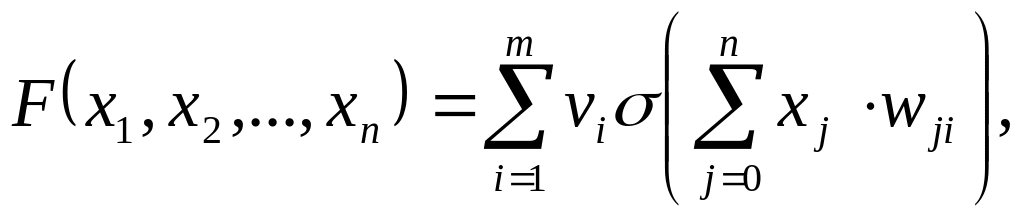
где

В 1957 году математик А. Н. Колмогоров доказал следующую теорему.

Теорема Колмогорова. Любая непрерывная функция F, опре­деленная на n-мерном единичном кубе, может быть представлена в виде суммы суперпозиций непрерывных и монотонных отображений еди­ничных отрезков:

где и - непрерывные функции, причем не зависят от функции F.

Эта теорема означает, что для реализации функций многих перемен­ных достаточно операций суммирования и композиции функций одной переменной. К сожалению, при всей своей математической красоте, те­орема Колмогорова малоприменима на практике. Это связано с тем, что функции - в общем случае негладкие и трудновычислимые; так­же неясно, каким образом можно подбирать функции для данной функции F. Роль этой теоремы состоит в том, что она показала принци­пиальную возможность реализации сколь угодно сложных зависимостей с помощью относительно простых автоматов типа нейронных сетей. Более значимые для практики результаты в этом направлении были получены только в 1989 году, зато одновременно несколькими исследователями.

Пусть - любая непрерывная функция, определенная на ограниченном множестве, и - любое сколь угодно малое число, означающее точность аппроксимации. Через обозначена сигмоидальная функция.

Теорема. Существуют число m, набор чисел , и набор чисел такие, что функция

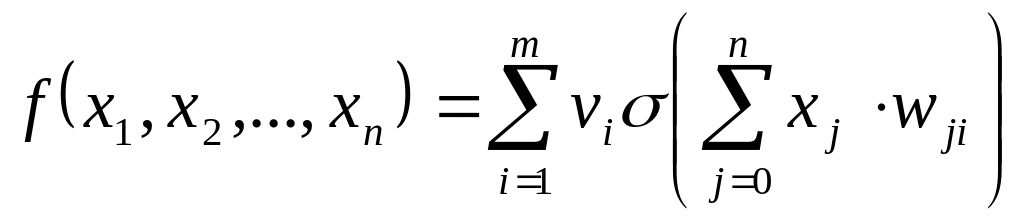
приближает данную функцию с погрешностью не более е на всей области определения.

Легко заметить, что эта формула полностью совпадает с выражением, полученным для функции, реализуемой нейросетью. В терминах теории нейросетей эта теорема формулируется так: любую непрерывную функ­цию нескольких переменных можно с любой точностью реализовать с помощью двухслойной нейросети с достаточным количеством нейронов в скрытом слое.