4.1.8. Нечеткие числа

Одной из основных областей применения нечеткой логики яв­ляется выполнение арифметических операций с нечеткими множествами, описывающими ту или иную модель или систему так, как если бы это были обычные числа. В качестве нечетких множеств при этом могут ис­пользоваться и термы лингвистических переменных, с помощью которых исследуемая система или модель была описана в силу невозможности применения обычных, количественных математических методов. А для снижения трудоемкости операций с нечеткими множествами используют специальный их тип — нечеткие числа.

Нечеткие числа — нечеткие переменные, определенные на числовой оси. Иначе говоря, нечеткое число определяется как нечеткое множе­ство A на множестве действительных чисел R с функцией принадлежно­сти ,где x — действительное число, т.е. .

Нечеткое число A нормально, если выпуклое, если для любых чисел выполняется условие Множество α-уровня нечеткого числа A определяется как Подмножество называется носителем нечеткого числа A (обозна­чается как Supp A), если

Нечеткое число унимодальное, если условие справедливо для одной и только одной действительной точки.

Выпуклое нечеткое число A называется нечетким нулем, если Нечеткое число A положительно, если и отрицательно, если

Примеры

4.13. Треугольным нечетким числом называется число, задаваемое функцией принадлежности (рис. 5.14)

Рис. 5.14. Функция принадлежно­сти

треугольного нечеткого числа

Используемое обозначение - носитель Supp A – интервал семантический смысл: «x приблизитель­но равно a».

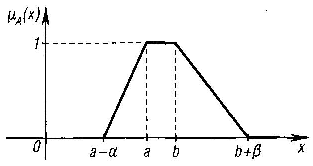
4.14. Трапецеидальным нечетким чи­слом называется число, задаваемое функ­цией принадлежности (рис. 5.15)

Рис. 5.15. Функция принадлежно­сти

трапецеидального числа

Используемое обозначение - носитель Supp A – интервал семантический смысл: «x лежит приблизитель­но в интервале ».

4.15. Опять вернемся к задаче интерпретации значений ЛП «воз­раст», таких как «молодой» возраст, «преклонный» возраст или «переходный» возраст. Определим «возраст» как ЛП (рис. 5.16). Тогда «молодой», «преклонный», «переходный» будут значениями этой лингвистической пере­менной. Более полно базовый набор значений ЛП «возраст» следующий:

Для ЛП «возраст» базовая шкала — это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории воз­раста. На рис. 5.17 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных не­четких множеств.

Рис. 5.16. Лингвистическая переменная «возраст» и нечеткие множества, определяю­щие ее значения

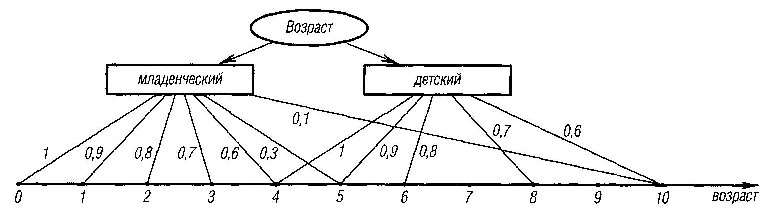
Рис. 5.17. Формирование нечетких множеств

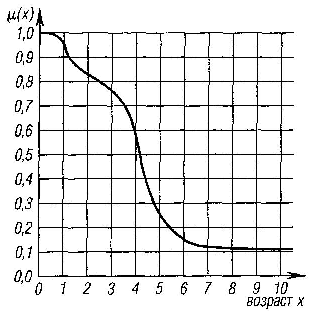
Рис. 5.18. График функции при­надлежности нечеткому множест­ву «младенческий» возраст

Например, определить значение НМ «младенческий» можно так:

Рисунок 5.18 иллюстрирует оценку этого НМ неким усредненным экспертом.

Этот эксперт ребенка до полугода с высокой степенью уверенности относит к младенцам Дети от полугода до четырех лет тоже причисляются к мла­денцам, но с меньшей степенью уверенности ), а в десять лет ребенка называют так только в очень редких случаях - к примеру, для девяностолетней бабушки и 15 лет может считаться младенчеством. Та­ким образом, нечеткие множества позволяют при определении понятия учитывать субъективные мнения отдельных индивидуумов.

Вопросы

4.14. Дайте определение нечеткой переменной. Приведите пример нечеткой переменной.

4.15. Дайте определение лингвистической переменной. Приведите пример.

4.16. Чем отличаются понятия нечеткой и лингвистической переменной?

4.17. Дайте определение нечеткого числа.

4.18. Являются ли нечеткое треугольное число, трапецеидальное нечеткое число нормальными числами?

4.19. Можно ли считать треугольное нечеткое число унимодальным? Трапецеидальное нечеткое число унимодальным? Приведите пример, ко­гда нечеткое число не соответствует этому определению.

Упражнения

4.8. Эксперт определяет рост ученика с помощью понятий «низкий рост», «средний рост», «высокий рост», при этом минимальный рост равен 145 см, максимальный— 175 см. Проведите формализацию такого описа­ния с помощью лингвистической переменной Укажите, какие объекты в данном примере обозначены через .

4.9. Постройте терм-множество и расширенное терм-множество в условиях предыдущего примера и изобразите их с помощью функций принадлежности.

4.10. Постройте график функции принадлежности нечеткого числа