4.1.6. Четкое множество α-уровня (или уровня α)

Множеством α-уровня нечеткого подмножества A универсаль­ного множества E называется четкое подмножество универсального множества E, определяемое в виде где

Примеры

4.8. Пусть , тогда

Достаточно очевидно следующее свойство: если , то .

4.9. Пусть

«малые числа»

«большие числа»

Тогда

«НЕ малые числа»

«малые числа И большие числа» ;

«малые числа ИЛИ большие числа» =

Приведенные определения операций над нечеткими множествами являются наиболее распространенными.

4.10. Пусть

;

;

.

Здесь: 1) , т. е. А содержится в В или В доминирует А, С несравнимо ни с А, ни с В, т. е. пары {А, С] и {В, С} — пары недоминируемых нечетких множеств;

2) ;

3) ,

4)

5)

6)

7) .

Вопросы

4.9. Дайте определение алгебраического произведения алгебра­ической суммы , дизъюнктивной суммы множеств A и B

4.10. Укажите, какие свойства выполняются для операций .

4.11. Дайте определение декартова произведения нечетких множеств.

4.12. Что называется четким множеством α-уровня?

4.13. Дайте определение выпуклой комбинации нечетких множеств

Упражнения

4.3. Даны множества: A —нечеткое множество «высокая зарплата», B — нечеткое множество «низкая зарплата»,

,

.

Назовите характеристики множеств A и B: высоту, носитель, точки перехода.

Найдите

4.4. Пусть даны множества:

;

;

.

Найдите сравнимые и несравнимые меж­ду собой множества и определите, какое мно­жество в какое включается, какие множества равны между собой. Найдите

Рис. 5.7. К упражнению 4.5

4.5. Пусть , A и B — нечеткие множества, заданные на универсальном мно­жестве Е. Пусть графики их характеристиче­ских функций принадлежности изображены на рис. 5.7—5.9. Какую операцию над множества­ми иллюстрирует выделенная на рис. 5.7 линия? Какая операция представлена на рис. 5.8? На рис. 5.9 штрих-пунктирной линией изоб­ражен график характеристической функции принадлежности множества A. Какое множе­ство представлено сплошной толстой линией?

Р ис. 5.8. К упражнению 4.5 Рис. 5.9. К упражнению 4.5

Рис. 5.10. К упражнению 4.6

4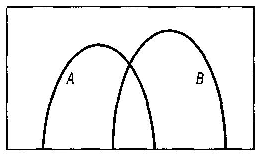 .6. Рассмотрим прямоугольную систему ко­ординат, на оси ординат которой откладывают­ся значения функций принадлежности, на оси абсцисс в произвольном порядке расположе­ны элементы универсального множества Е. На рис. 5.10 представлены графики характеристиче­ских функций принадлежности множеств A и B. Изобразите на рисунке графики характери­стических функций принадлежности нечетких множеств .

4.7. Пусть и

Найдите

4.1.7. Нечеткая и лингвистическая переменные

Понятия нечеткой и лингвистической переменных использу­ются при описании объектов и явлений с помощью нечетких множеств.

Лингвистические переменные (ЛП) были предложены как средство моделирования нечеткости естественного человеческого языка, в котором границы между отдельными понятиями часто неявны и размыты. По сути, лингвистические переменные стали предпосылкой к развитию всей нечеткой логики и теории нечетких множеств.

В настоящее время ЛП являются распространенным способом опи­сания сложных систем, параметры которых по каким-либо причинам должны рассматриваться не с количественных позиций, а как качествен­ные. При этом лингвистические переменные дают возможность поста­вить в соответствие качественным значениям некоторую количественную интерпретацию с заданной долей уверенности, что позволяет обрабаты­вать качественные данные на компьютере. Как следствие, другой сферой применения ЛП является нечеткий логический вывод, отличие которого от обычного заключается в том, что истинность логических высказыва­ний описывается не двумя значениями ЛОЖЬ и ИСТИНА или 0 и 1, а множеством значений в интервале.

Для иллюстрации перечисленных положений продолжим рассмотре­ние примера о возрасте человека. Как правило, для описания человека достаточно общей качественной оценки его возраста в виде фраз «моло­дой», «переходный», «пожилой» и т. д. Причем за каждым из этих назва­ний скрывается некоторая совокупность конкретных значений, которая у разных людей может различаться, но в целом является общеприня­той. Таким образом, при описании возраста неосознанно используется некоторый набор нечетких множеств, с помощью которых описывается конкретное понятие. Такой набор и получил название лингвистической переменной, для которой в нечеткой логике существуют особые правила создания и формального описания.

В основе понятия лингвистической переменной лежит термин «не­четкая переменная», обозначающий нечеткое множество, которому было присвоено некоторое наименование.

Нечеткая переменная характеризуется тройкой (α, X, A), где

α — наименование переменной;

X — универсальное множество (область определения а),

A — нечеткое множество на X, описывающее ограничения (т. е. ) на значения нечеткой переменной α.

Например, рассмотренные выше нечеткие множества «молодой» и «пожилой» являются нечеткими переменными, поскольку представляют собой не просто абстрактные отображения действительной оси в ин­тервал, а отображения, имеющие за собой определенный смысл, выражающийся как в названии, так и в аналитическом выражении функ­ции принадлежности.

Лингвистической переменной называется набор (β,T,X,G,M), где

β — наименование лингвистической переменной;

T —множество ее значений, представляющих собой наименования нечетких переменных, областью определения каждой из которых явля­ется множество X; множество Т называется базовым терм-множеством лингвистической переменной;

G — синтаксическая процедура, позволяющая оперировать элемента­ми множества T, в частности, генерировать новые значения; множество , где G(T) —множество сгенерированных значений, называется расширенным терм-множеством лингвистической переменной;

M — семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т. е. сформировать соответствующее нечеткое множество.

Или, другими словами, лингвистическую переменную можно задать как пятерку (β,T(β), X, G, M), где

β — название лингвистической переменной;

T(β) — базовое терм-множество лингвистической переменной β, т. е. множество названий лингвистических значений переменной , каждому из которых соответствует нечеткая переменная α с областью определения в виде универсального множества X;

G — синтаксическое правило (обычно грамматика), порождающее значения лингвистической переменой;

M — семантическое правило, которое ставит в соответствие каждой нечеткой переменной α ее смысл, т. е. нечеткое подмножество универ­сального множества X.

Приведем несколько примеров лингвистических переменных.

Примеры

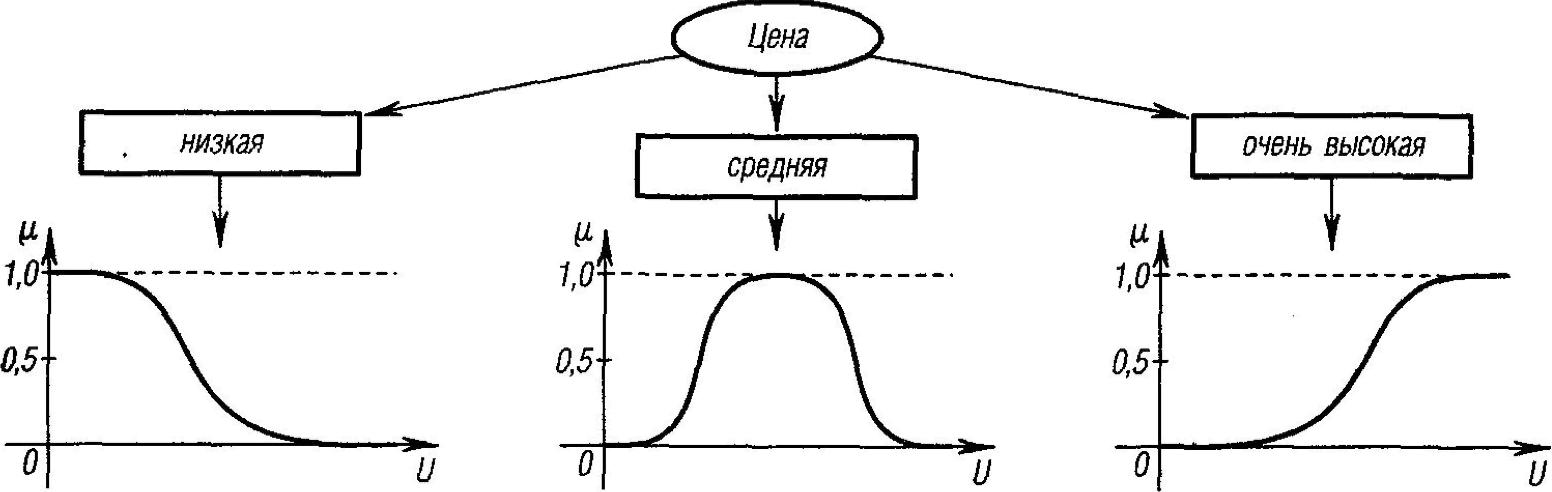
4.11. На рис. 5.11 представлена графическая интерпретация лингви­стической переменной «цена».

Рис. 5.11. Лингвистическая переменная «цена»

4.12. Пусть эксперт определяет толщину выпускаемого изделия с по­мощью понятий «малая толщина», «средняя толщина» и «большая толщина», при этом минимальная толщина равна 10 мм, а максимальная — 80 мм.

Формализация такого описания может быть проведена с помощью лингвистической переменной (β, T, X, G, M), где

β — толщина изделия;

T = {«малая толщина», «средняя толщина», «большая толщина»};

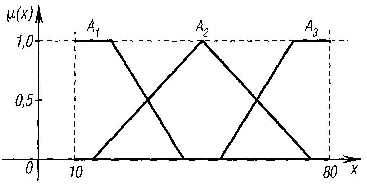
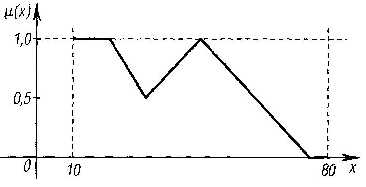
Рис. 5.12. Функции принадлежности нечетких множеств: «малая толщина» = , «средняя толщина» = , «большая толщина»=

Рис. 5.13. Функция принадлежности не­четкого множества «малая ИЛИ средняя толщина»=

G - процедура образования новых термов с помощью связок И, ИЛИ и модификаторов типа ОЧЕНЬ, НЕ, СЛЕГКА и т. п. (например: «малая ИЛИ средняя толщина», «ОЧЕНЬ малая толщина»);

M - процедура задания на универсальном нечетких подмножеств = «малая толщина», = «средняя толщина», = «большая толщина», а также нечетких множеств для термов из G(T).

Замечание.

Наряду с рассмотренными выше базовыми значе­ниями лингвистической переменной «толщина» возможны значения, зависящие от области определения X. В данном случае значения лингвистической переменной «толщина» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», т. е. в виде нечетких чисел.

Элементы базового терм-множества и расширенного терм-множества в условиях данного примера можно характеризовать функциями принад­лежности, приведенными на рис. 5.12, 5.13.