По характеру изменения ёмкости:

1. Конденсаторы постоянной ёмкости (постоянные конденсаторы)

2. Конденсаторы переменной ёмкости (переменные конденсаторы)

3. Подстроечные конденсаторы

По способу защиты:

1. Незащищённые конденсаторы

2. Защищённые конденсаторы

3. Неизолированные конденсаторы

4. Изолированные конденсаторы

5. Уплотнённые конденсаторы

6. Герметизированные конденсаторы

По виду диэлектрика:

1. C газообразным диэлектриком

2. C оксидным диэлектриком

3. C неорганическим диэлектриком

4. C органическим диэлектриком

Конденсаторы постоянной ёмкости (постоянные конденсаторы) подразделяются на высокочастотные и низкочастотные. Постоянные конденсаторы не могут изменять свою ёмкость в процессе работы, то есть их ёмкость является постоянной (точнее, она может колебаться в небольших пределах в зависимости от температуры, но это в пределах допуска). Конденсаторы переменной ёмкости (переменные конденсаторы) могут изменять свою ёмкость в процессе работы. Как известно, ёмкость конденсатора зависит от площади его обкладок и расстояния между ними. Эти параметры можно изменять различными способами. Вы наверняка пользовались аналоговыми радиоприёмниками, в которых переменные конденсаторы используются для настройки на радиостанцию. Подстроенные конденсаторы также могут изменять свою ёмкость. Переменные конденсаторы отличаются от подстроечных тем, что их ёмкость можно изменять во время работы устройства, в то время как подстроечные конденсаторы используются обычно только при настройке аппаратуры на заводе. Кроме этого конденсаторы можно разделить на полярные и неполярные (хотя по этим признакам их обычно не классифицируют). Полярные конденсаторы могут работать только в цепях постоянного тока и требуют строгого соблюдения полярности при подключении (плюс подключается к выводу со знаком плюс, минус, соответственно - к выводу со знаком минус). При не соблюдении этого требования такой конденсатор может выйти из строя. Неполярные конденсаторы могут работать в цепях как постоянного, так и переменного тока. Такие конденсаторы можно подключать без учёта полярности напряжения.

Диэлектрики. Диэлектрики – вещества, обладающие малой электропроводностью, т.к. у них очень мало свободных заряженных частиц – электронов и ионов. Эти частицы появляются в диэлектриках только при нагреве до высоких температур. Существуют диэлектрики газообразные (газы, воздух), жидкие (масла, жидкие органические вещества) и твердые (парафин, полиэтилен, слюда, керамика и т.п.).При наложении электрического напряжения в диэлектрике, представляющем сложную электрическую систему, протекают разнообразные электрические процессы, связанные с его поляризацией, электрической проводимостью. В случае очень большого напряжения может произойти разрушение диэлектрика, называемое пробоем. Эти процессы определяют свойства диэлектриков, а, следовательно, надежность их работы в радиоустройствах, поэтому рассмотрим эти процессы. Электрическое поле в диэлектрике. Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями (рис. 2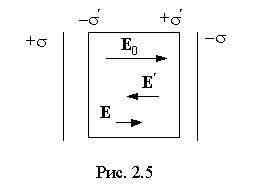 .5). Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна  ,где   - поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле  , которое направлено против внешнего поля  .

,

где   - поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика .

Поверхностная плотность связанных зарядов   меньше плотности   свободных зарядов, и не все поле E₀ компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика  . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее  . Таким образом, ,где   - диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума  , для диэлектриков  .

Теорема Остроградского-Гаусса для потока вектора индукции эл.Поля.

Теорема Остроградского Гаусса – поток вектора эл. смещения через произвольную замкнутую поверхность (Фе=”DndS) равен суммарному свободному заряду, находящемуся внутри этой поверхности. Фе=Sqсвоб

Условия на границе раздела двух диэлектриков. Воспользуемся теоремой о циркуляции электрического поля:

. Выберем на границе раздела сред замкнутый прямоугольный контур длины l и ширины D .Частично этот контур проходит в первой среде, а частично — во второй. Циркуляция вектора напряжённости электрического поля по этому контуру равна нулю. .

Здесь мы учли, что вклад в циркуляцию участков D стремится к нулю, при стремящейся к нулю ширине контура D. Отсюда следует, что:                .                 

При переходе через границу раздела сред, касательная составляющая вектора напряжённости не меняется.

Но по условию свободные заряды на границе раздела сред отсутствуют: q_{свободн} = 0, поэтому: .

Электрострикция. Электрострикция — эффект изменения линейных размеров вещества при приложении к нему электрического поля. Наблюдается абсолютно во всех веществах (в отличие от пьезоэффекта, который существует лишь в кристаллах с определённой симметрией).Связь между деформацией и электрическим полем является квадратичной. Линейная связь между деформацией и электрическим полем наблюдается в пьезоэлектриках. Наиболее высокие значения электрострикции наблюдаются в веществах, получивших название сегнетоэлектрические релаксоры. Формально, электрострикционный коэффициент — это тензор четвёртого ранга ( ), зависящий от механического напряжения (тензор второго ранга  ) и поляризации (тензоры первого ранга  ,  ).

Пьезоэлектрический эффект. Пьезоэлектрический эффект — эффект возникновения поляризации диэлектрика под действием механических напряжений (прямой пьезоэлектрический эффект). Существует и обратный пьезоэлектрический эффект — возникновение механических деформаций под действием электрического поля. Прямой и обратный пьезоэлектрический эффекты наблюдаются в одних и тех же кристаллах — пьезоэлектриках. Прямой эффект открыт братьями Жаком и Пьером Кюри в 1880 г.^[1] Обратный эффект был предугадан в 1881 г. Липпманом на основе термодинамических соображений и в том же году экспериментально подтверждён братьями Кюри. Пьезоэффекта нельзя путать с электрострикцией. В отличие от электрострикции, прямой пьезоэффект наблюдается только в кристаллах без центра симметрии. Хотя в классе 432 кубической сингонии нет центра симметрии, пьезоэлектричество в нём также невозможно. Следовательно, пьезоэффект может наблюдаться у диэлектрических кристаллов, принадлежащим только к одному из 20 классов точечных групп.

Основные уравнения электростатики диэлектриков. Основное уравнение имеет вид где   — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить   на две части. Обозначим снова через   заряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем  . В  этом случае уравнение приобретает вид или Уравнение для ротора от  , конечно, не меняется: .    Подставляя   из уравнения ,получаем более простое уравнение: .

Объемная плотность энергии электростатического поля Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна   . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем С учетом, что   и  или

Электрический Ток в Вакууме Если два электрода поместить в герметичный сосуд и удалить из сосуда воздух, то электрический ток в вакууме не возникает - нет носителей электрического тока. Американский ученый Т. А. Эдисон (1847-1931) в 1879 г. обнаружил, что в вакуумной стеклянной колбе может возникнуть электрический ток, если один из находящихся в ней электродов нагреть до высокой температуры. Явление испускания свободных электронов с поверхности нагретых тел называется термоэлектронной эмиссией. Работа, которую нужно совершить для освобождения электрона с поверхности тела, называется работой выхода. Явление термоэлектронной эмиссии объясняется тем, что при повышении температуры тела увеличивается кинетическая энергия некоторой части электронов в веществе. Если кинетическая энергия электрона превысит работу выхода, то он может преодолеть действие сил притяжения со стороны положительных ионов и выйти с поверхности тела в вакууме. На явлении термоэлектронной эмиссии основана работа различных электронных ламп

Термоэлектронная эмиссия  — явление испускания электронов нагретыми телами. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет, и явление термоэлектронной эмиссии становится заметным..

Вторичная и автоэлектронная эмиссия. Электронная эмиссия- это явление испуская электронов поверхностью твердого тела или жидкости. При бомбардировке поверхностей металлов, полупроводни­ков или диэлектриков пучком электронов наблюдается испускание вторичных электронов. Это явление называется вторичной электрон­ной эмиссией (в электронных лампах его чаще называют динатрон­ным эффектом). В пучке эмитируемых электронов наблюдаются три, группы электронов; 1) электроны, упруго отраженные поверхностью эмиттера, 2) неупругоотраженные электроны, 3) вторичные электроны, т. е. такие электроны, которые выбиваются из эмиттера первичными электронами Вторичная электронная эмиссия из толстых слоев металла всегда больше, чем из тонких металлических пленок, нанесенных на поверх­ность стекла. С увеличением толщины пленки до определенного предела эмиссия возрастает. Однако, начиная с этого предела, она становится такой же, как и у толстых металлических тел. Поэ­тому, экспериментируя с пленками, можно оценить толщину поверх­ностного слоя металла, из которого происходит эмиссия вторичных электронов..

Электрический ток в газе. В естественном состоянии газ – диэлектрик. В обычных условиях в газе почти нет свободных носителей заряда, движение которых могло бы создать электрический ток. Для того, чтобы газ стал поводящим, необходимо создать в нем свободные заряженные частицы, т. е. превратить нейтральные молекулы (или атомы) в ионы. Электрический ток через газ называют газовым разрядом. Газовый разряд — совокупность процессов, возникающих при протекании электрического тока через вещество, находящееся в газообразном состоянии. Обычно протекание тока становится возможным только после достаточной ионизации газа и образования плазмы. Ионизация происходит за счёт столкновений электронов, ускорившихся в электромагнитном поле, с атомами газа.

процессы ионизации и рекомбинации Ионизация — эндотермический процесс образования ионов из нейтральных атомов или молекул. Положительно заряженный ион образуется, если электрон в атоме или молекуле получает достаточную энергию для преодоления потенциального барьера, равную ионизационному потенциалу. Отрицательно заряженный ион, наоборот, образуется при захвате дополнительного электрона атомом с высвобождением энергии. Рекомбинация — исчезновение носителей заряда в результате столкновения зарядов противоположных знаков (при «низких» скоростях).В полупроводниках возможны следующие варианты рекомбинации: межзонная — непосредственный переход электронов в валентную зону, существенна в собственных полупроводниках и полупроводниках с узкой запрещённой зоной с минимальным количеством дефектов; через промежуточные уровни в запрещённой зоне, существенна в примесных полупроводниках.; В образцах с большим значением поверхности на единицу объёма значительно возрастает роль рекомбинации на поверхностных состояниях (поверхностной рекомбинации) При рекомбинации носителей выделяется энергия, которая передаётся частицам (в том числе квази-). В зависимости от типа частиц-«приёмников» выделяются: излучательная рекомбинация — энергия уносится фотонами; безызлучательная рекомбинация — энергия передается фононам решетки или другим частицам (Оже-рекомбинация).

 Понятие о плазме В газовом разряде возникает большое количество положительных ионов вследствие высокой эффективности ударной ионизации, причем концентрация ионов и электронов одинакова. Такая система из электронов и положительных ионов, распределенных с одинаковой концентрацией, называется плазмой. Плазма, возникающая в газовом разряде, носит название газоразрядной; к ней относятся положительный столб тлеющего разряда, канал искрового и дугового разрядов. Положительный столб представляет собой так называемую неизотермическую плазму. В такой плазме средние кинетические энергии электронов, ионов и нейтральных молекул (атомов) различны. Важнейшие свойства плазмы:

•      сильное взаимодействие с внешними магнитными и электрическими полями, связанное с ее высокой электропроводностью;

•      специфическое коллективное взаимодействие частиц плазмы, осуществляющееся через усредненные электрические и магнитные поля, которые создают сами эти частицы;

•      благодаря коллективным взаимодействиям плазма ведет себя как своеобразная упругая среда, в которой легко возбуждаются и распространяются различного рода колебания и волны (например, ленгмюровские колебания плазмы);

•      во внешнем магнитном поле плазма ведет себя как диамагнитная среда;

•      удельная электрическая проводимость σ полностью ионизованной плазмы не зависит от плотности плазмы и увеличивается с ростом термодинамической температуры, пропорционально  . При Т ≥ 10⁷ К, σ столь велика, что плазму можно приближенно считать идеальным проводником ( ).

электропроводность плазмы В силу хорошей электрической проводимости плазмы разделение положительных и отрицательных зарядов невозможно на расстояниях больших дебаевской длины и временах больших периода плазменных колебаний. Примером не квазинейтральной плазмы является пучок электронов. Однако плотность нейтральных плазм должна быть очень мала, иначе они быстро распадутся за счёт кулоновского отталкивания.

Электролиты. Электролит — вещество, расплав или раствор которого проводит электрический ток вследствие диссоциации на ионы, однако само вещество электрический ток не проводит. Примерами электролитов могут служить растворы кислот, солей и оснований. Электролиты — проводники второго рода, вещества, которые в растворе (или расплаве) состоят полностью или частично из ионов и обладающие вследствие этого ионной проводимостью. В растворах некоторых электролитов диссоциирует лишь часть молекул. Для количественной характеристики электролитической диссоциации было введено понятие степени диссоциации^[1]. Исходя из степени диссоциации все электролиты делятся на две группы 1)Сильные электролиты — электролиты, степень диссоциации которых в растворах равна единице (то есть диссоциируют полностью) и не зависит от концентрации раствора. Сюда относятся подавляющее большинство солей, щелочей, а также некоторые кислоты (сильные кислоты, такие как: HCl, HBr, HI, HNO₃). 2)Слабые электролиты — степень диссоциации меньше единицы (то есть диссоциируют не полностью) и уменьшается с ростом концентрации. К ним относят воду, ряд кислот (слабые кислоты), основания p-, d-, и f- элементов. Между этими двумя группами четкой границы нет, одно и то же вещество может в одном растворителе проявлять свойства сильного электролита, а в другом — слабого. Электролиз. Электролиз — физико-химический процесс, состоящий в выделении на электродах составных частей растворённых веществ или других веществ, являющихся результатом вторичных реакций на электродах, который возникает при прохождении электрического тока через раствор либо расплав электролита.

Упорядоченное движение ионов в проводящих жидкостях происходит в электрическом поле, которое создается электродами — проводниками, соединёнными с полюсами источника электрической энергии. Анодом при электролизе называется положительный электрод, катодом — отрицательный^[1]. Положительные ионы — катионы — (ионы металлов, водородные ионы, ионы аммония и др.) — движутся к катоду, отрицательные ионы — анионы — (ионы кислотных остатков и гидроксильной группы) — движутся к аноду. Явление электролиза широко применяется в современной промышленности. В частности, электролиз является одним из способов промышленного получения алюминия, водорода, а также гидроксида натрия, хлора, хлорорганических соединений диоксида марганца^[2], пероксида водорода. Большое количество металлов извлекаются из руд и подвергаются переработке с помощью электролиза (электроэкстракция, электрорафинирование). Также, электролиз является основным процессом, благодаря которому функционирует химический источник тока. Электролиз находит применение в очистке сточных вод (процессы электрокоагуляции, электроэкстракция, электрофлотации).

Законы электролиза

первый закон Фарадея В 1832 году Фарадей установил, что масса m вещества, выделившегося на электроде, прямо пропорциональна электрическому заряду q, прошедшему через электролит: если через электролит пропускается в течение времени t постоянный ток с силой тока I. Коэффициент пропорциональности   называется электрохимическим эквивалентом вещества. Он численно равен массе вещества, выделившегося при прохождении через электролит единичного электрического заряда, и зависит от химической природы вещества. Второй закон Фарадея Электрохимические эквиваленты различных веществ относятся, как их химические эквиваленты.

Химическим эквивалентом иона называется отношение молярной массы A иона к его валентности z. Поэтому электрохимический эквивалент где   — постоянная Фарадея. Второй закон Фарадея записывается в следующем виде: где   — молярная масса данного вещества, образовавшегося (однако не обязательно выделившегося — оно могло и вступить в какую-либо реакцию сразу после образования) в результате электролиза, г/моль;   — сила тока, пропущенного через вещество или смесь веществ (раствор, расплав), А;   — время, в течение которого проводился электролиз, с;   — постоянная Фарадея, Кл·моль⁻¹;   — число участвующих в процессе электронов, которое при достаточно больших значениях силы тока равно абсолютной величине заряда иона (и его противоиона), принявшего непосредственное участие в электролизе (окисленного или восстановленного). Однако это не всегда так; например, при электролизе раствора соли меди(II) может образовываться не только свободная медь, но и ионы меди(I) (при небольшой силе тока).

Электрохимические потенциалы — физическая величина, связывающая химический потенциал (μ) и электрический потенциал (φ) некоторой электрохимической системы соотношением: A = μ + e·φ

где А — работа, нарушающая электрохимическое равновесие системы; e — элементарный заряд частицы. Для растворенного вещества:μ = μ₀ + R*T*lnC + z*F*φ где μ₀ - Стандартный химический потенциал, зависящий от природы растворителя. С - концентрация вещества R - газовая постоянная T – температура z - валентность иона F - число Фарадея φ - электрический потенциал

Электропроводность металлов. Электрическая проводимость (электропроводность, проводимость) — способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению. В СИ единицей измерения электрической проводимости является сименс (называемая также в некоторых странах Мо).

Уровни Ферми Для начала, нужно рассмотреть понятие энергии Ферми, так как это понятие, само по себе, есть ответом на Ваши вопросы.  Энергия Ферми - максимальная энергия электронов при температуре в 0 К. Энергия Ферми растет с увеличением количества электронов в квантовой системе и, соответственно, уменьшается с уменьшением количества электронов (фермионов). Это обусловливается возникающим интенсивным обменным и электростатическим взаимодействием в области перекрытия зарядовых плотностей волновых функций электронов при росте количества электронов. Энергия и импульс Ферми есть граничными энергией и импульсом перехода электрона в свободное состояние. Поверхность в пространстве импульсов при 0 К, под которой все квантовые состояния заняты (то есть, нахождение электронов на заполненных орбиталях), есть поверхностью Ферми. При увеличении температуры возникает корреляция атомов и выделяются фононы, которые поглощаются электронами. В результате импульс электронов превышает граничный импульс Ферми, и они переходят в разрешенную зону (формально, есть квазисвободными частицами). Уровень Ферми в полупроводниках различных типов проводимости  Следует заметить, что в любом полупроводнике при стремлении температуры к абсолютному нулю уровень Ферми находится посередине запрещенной зоны. Но при повышении температуры в примесных полупроводниках он смещается либо вверх, либо вниз. Причина этого - в переходе электронов с валентной зоны в зону проводимости или наоборот, что обусловливает изменение энергии зоны проводимости и последующее смещение уровня Ферми (что Вас, собственно, и интересует). В случае с беспримесными полупроводниками, уровень Ферми при любой температуре проходит по середине запрещенной зоны. В случае с n-полупроводниками, количество электронов в зоне проводимости больше, чем у беспримесных полупроводников, поэтому средняя энергия электронов в зоне проводимости, в силу того же роста суммарной энергии системы при увеличении количества фермионов, повышается. Из-за этого, чтобы покинуть валентную зону и перейти в зону проводимости, электрону в n-полупроводнике требуется больше энергии, чем электрону из беспримесного полупроводника. Потому уровень Ферми находится выше средины запрещенной зоны. Формально, уровень Ферми в n-полупроводниках лежит посередине между дном зоны проводимости и донорным уровнем. В случае с p--полупроводниками, наблюдается обратная ситуация: чем большая концентрация акцепторов (например, атомов In), тем меньшая средняя плотность энергии электронов в зоне проводимости полупроводника, тем меньше средняя энергия на один электрон, и тем меньшая энергия требуется электрону, чтобы перейти в зону проводимости. Потому уровень Ферми находится ниже средины запрещенной зоны. явление сверхпроводимости Сверхпроводимость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Известны несколько десятков чистых элементов, сплавов и керамик, переходящих в сверхпроводящее состояние. Сверхпроводимость — квантовое явление. Оно характеризуется также эффектом Мейснера, заключающимся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

Электропроводимость полупроводников. -------

Понятие дырочной проводимости. ДЫРОЧНАЯ ПРОВОДИМОСТЬ (проводимость p-типа) – проводимость полупроводника, в котором основными носителями тока являются дырки. Дырочной проводимостью обладают полупроводники с акцепторной примесью (точнее, когда концентрация атомов акцепторной примеси превышает концентрацию атомов донорной примеси).

Электромагнитные явления на границе раздела двух сред -------

Магнитное поле тока. Магнитное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^[2] Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции   (вектор индукции магнитного поля)^[3][4]. С математической точки зрения   — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина). Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал. Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Электромагнитное взаимодействие движущихся зарядов и элементарных токов -------

Индукция магнитного поля Магнитная индукция   — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой   магнитное поле действует на заряд  , движущийся со скоростью  .

Более конкретно,   — это такой вектор, что сила Лоренца  , действующая со стороны магнитного поля^[1] на заряд  , движущийся со скоростью  , равна где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора  перпендикулярно им обоим и направлено по правилу буравчика).Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Закон Био-Савара-лапласа Закон Био́— Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Допустим требуется найти модуль магнитной индукции в центре очень тонкой (все витки уложены вблизи одной окружности) катушки с числом витков  , по которой течет ток  . Найдём магнитную индукцию, создаваемую одним витком катушки. Из формулы получим модуль магнитной индукции как где   - как следствие, радиус катушки - константа,   - угол между вектором   и   (элемента витка), ввиду взаимной перпендикулярности, всегда равен  . Проинтегрировав обе части получаем где   - сумма длин всех элементов проводника витка или длина окружности, тогда Так как в катушке содержится   витков, то суммарный модуль магнитной индукции равен

Циркуляция вектора магнитной индукции. --------

Вихревой характер магнитного поля Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

Поток вектора магнитной индукции. Поток магнитной индукции - поток вектора магнитной индукции через некоторую поверхность; величина, равная произведению: - модуля вектора магнитной индукции; на - площадь поверхности; и на  - косинус угла между вектором магнитной индукции и нормалью к поверхности. В СИ единицей магнитного потока является вебер.

Закон Ампера.— закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Модуль силы Ампера можно найти по формуле:

Работа сил магнитного поля. --------

Сила Лоренца- это сила действующая на одну заряженную частицу. Fл=qvBsina. Угол а равен углу между скоростью и вектором магнитной индукции. *Направление силы Лоренца, действующей на положительно заряженную частицу, так же может быть найденного по правилу левой руки или по правилу буравчика. *При движении заряженной частицы в магнитном поле сила Лоренца работу не совершает. *Период обращения частицы в однородном магнитном поле T=2ПR/V=2Пм/qB.

Эффект Холла— явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.

Закон полного тока Закон полного тока является одним из важнейших законов, устанавливающим неразрывную связь между электрическим током и магнитным полем. Из него следует, что любая магнитная линия обязательно охватывает электрический ток и, наоборот, электрический ток всегда окружен магнитным полем. один из осн. законов электромагнитного поля. Согласно П. т. з., циркуляция вектора Н напряжённости магнитного поля вдоль произвольного замкнутого контура L, проведённого в поле, равна полному электрич. току сквозь поверхность 5, натянутую на контур L:ф_L.(H,dl)= интеграл_s(J,dS). Здесь J - вектор плотности полного тока, равный геом. сумме векторов плотностей тока проводимости и тока смещения.

Намагниченность магнетиков -----------

Магнитные моменты атомов и молекул --------------------

Диамагнетизм— один из видов магнетизма, который проявляется в намагничивании вещества навстречу направлению действующего на него внешнего магнитного поля. Диамагнетизм свойствен всем веществам. Диамагнетизм можно рассматривать как следствие индукционных токов, наводимых в заполненных электронных оболочках ионов внешним магнитным полем. Эти токи создают в каждом атоме индуцированный магнитный момент, направленный, согласно правилу Ленца, навстречу внешнему полю (независимо от того, имелся ли первоначально собственный момент или нет и как он был ориентирован). Диамагнетизм, однако, невозможно описать с позиции только классической физики, это предельно квантовомеханическое явление.^[1] Идеальный диамагнетизм носит некооперативный характер и характеризуется отрицательной, не зависящей от температуры магнитной восприимчивостью. Диамагнетизм входит в состав любого магнитного состояния вещества, но он обычно пренебрежимо мал по сравнению с магнетизмом, обусловленным наличием спонтанных магнитных моментов в системе. У чисто диамагнитных веществ электронные оболочки (молекул) не обладают постоянным моментом. Моменты, создаваемые отдельными электронами в таких в отсутствие внешнего поля взаимно скомпенсированы. В частности, это имеет место в ионах и молекулах с целиком заполненными электронными оболочками, например, в инертных газах, в молекулах.Примерами чисто диамагнитных твёрдых тел (диамагнетиков) в классе кристаллических металлов и диэлектриков могут служить, соответственно, Cu и NaCl, а в классе аморфных твёрдых тел — SiO₂.

Парамагнетизм Парамагнетизм - (от пара ... и магнетизм), свойство вещества намагничиваться во внешнем магнитном поле в направлении поля. Парамагнетизмом обладают вещества (парамагнетики), атомы (ионы) которых имеют магнитный момент, но в которых отсутствует самопроизвольная намагниченность. При намагничивании атомные магнитные моменты выстраиваются по направлению поля (в отсутствие поля они дезориентированы тепловым движением). Магнитная восприимчивость парамагнитного вещества ?>0; у многих веществ она не зависит от поля, но сильно зависит от температуры Т (см. Кюри закон), у щелочных металлов зависимость ? от Т слаба (см. Паули парамагнетизм). При температурах выше Кюри точки (или Нееля точки) ферро-, антиферро- и ферримагнетики парамагнитны (см. Кюри - Вейса закон). Кроме атомного существует также ядерный парамагнетизм. ; 

ферромагнетизм Ферромагнетизм - , магнитоупорядоченное состояние макроскопических объемов вещества (ферромагнетика), в котором магнитные моменты атомов (ионов) параллельны и одинаково ориентированы. Эти объемы - домены - обладают магнитным моментом Ms (самопроизвольной намагниченностью) даже при отсутствии внешнего намагничивающего поля. Для ферромагнетиков во внешнем магнитном поле характерны: нелинейность кривой намагничивания и магнитный гистерезис при перемагничивании. Значение Ms максимально при Т = 0К, с увеличением температуры Ms уменьшается и обращается в нуль в Кюри точке, выше которой вещество становится парамагнитным. ; 

Явление электромагнитной индукции — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

ЭДС индукции Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ). В замкнутом контуре ( ) тогда ЭДС будет равна: , где   — элемент длины контура. ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы не потенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки). Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи. Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.

Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем). Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции. Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  : .Коэффициент пропорциональности   называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Установление и исчезновение тока в цепи --------

Энергия магнитного поля Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна                                      W_м = LI²/ 2

Основные понятия и аксиомы статики

Аксиомы статики1)Аксиома инерции- под действие взаимно уравновешенные системы сил тело находится в состоянии покоя или равномерного прямолинейного движения; 2)Аксиома двух сил- если тело под действием двух сил находится в равновесии, то эти силы равны по модулю и направлены под одной прямо в противоположные стороны.3)Аксиома присоединения- если к заданной системе сил присоединить (или изьять) взаимно уравновешенную систему сил, то кинематическое состояние тела не изменить. 4)Аксиома параллелограмма – равнодействующая двух пересекающихся сил равна диагонали параллелограмма, построенного на этих силах как на сторонах. 5)Аксиома действия и противодействия- всякому действию соответствует равное и противоположное противодействие( 3 закон Ньютона) 6)Аксиома отвердевания- равновесие деформируемого тела сохраняется при его затвердевании.

Способы сложения двух сил

Разложение силы на составляющие. Мы уже знаем, как отыскать равнодействующую двух или нескольких заданных сил, направления которых пересекаются. Не менее важна для практики  задача о разложении силы на составляющие, т. е. задача   отыскания   нескольких сил, равнодействующей которых была бы данная сила. Эта задача может приводить к различным решениям, подобно тому как это имеет место при разложении вектора перемещения.

Чтобы задача о разложении силы стала определенной (т. е. имела бы только одно решение), необходимы дополнительные указания. Например, если заданы величина и направление одной из составляющих или два направления, по которым должны действовать составляющие, и т. п., то операция разложения силы на две составляющие становится вполне определенной и сводится к простому геометрическому построению.

П усть, например, мы хотим разложить силу F  на две составляющие, лежащие в одной плоскости с F¹ и направленные вдоль прямых АВ и АС (рис. 104). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные АВ и АС. Отрезки F₁ и F₂ изобразят искомые силы.

Обычно в стоящих перед нами механических задачах содержатся указания на то, как целесообразнее разложить силу на составляющие. Часто условия задачи прямо указывают те направления, по которым нужно найти составляющие данной силы. Например, чтобы отыскать силы натяжения тросов, на которых висит груз, нужно силу тяжести Р груза разложить на составляющие Р₁ и Р₂ по направлениям этих тросов (рис. 105). Натяжения тросов должны уравновесить эти составляющие. Как легко видеть, чем больше угол между тросами, тем больше окажутся силы натяжения тросов. Поэтому если расстояние между опорами тросов велико, то даже небольшой груз, если он висит немного ниже опор, вызывает очень большое натяжение тросов. Этим объясняется, почему гололед или иней иногда обрывает туго натянутые провода.

При разложении силы на три или большее число составляющих увеличивается и число условий, необходимых для того, чтобы разложение было выполнено однозначно.

К инематика точки Кинематика точки – это раздел кинематики, в котором исследуют механическое движение материальной точки. Основная задача кинематики точки состоит в следующем:1) задать закон движения точки, т.е. указать правило, в соответствии с которым можно однозначно определить положение точки в пространстве в любой момент времени по отношению к выбранной системе отсчета;2) по заданному закону движения точки определить все кинематические характеристики ее движения. К характеристикам движения относят траекторию, скорость и ускорение точки. Траектория точки – непрерывная пространственная кривая, которую точка описывает в процессе движения. Если траекторией является прямая линия, то движение называют прямолинейным, если кривая – криволинейным.1.1. Способы задания движения точки Используют три основных способа задания движения точки: векторный, координатный и естественный.           Векторный способ. Положение движущейся точки М в любой момент времени можно определить с помощью ее радиус-вектора, проведенного из центра О, связанного с телом отсчета, в точку М (рис. 1.1). Чтобы задать движение векторным способом, необходимо определить векторную функцию времени в виде:

                                             (1.1)

Зависимость (1.1) называют уравнением движения точки в векторной форме. Начало радиус-вектора движущейся точки находится в точке О, а конец его перемещается по траектории вместе с точкой М. Геометрическое место концов радиус-вектора, т.е. годограф этого вектора, определяет траекторию движущейся точки.

Координатный способ. С телом отсчета связывают прямоугольную систему декартовых координат, при этом положение точки определяют ее координатами, которые являются скалярными функциями времени (рис. 1.2):

                                                   (1.2)

Уравнения (1.2) называют уравнениями движения точки в координатной форме. Они являются параметрическими уравнениями траектории точки. Исключив из этих уравнений параметр – время, можно получить уравнение траектории.

Между способами задания движения точки имеется связь. Так, если начало декартовой системы координат совпадает с центром, из которого проводится радиус-вектор точки при векторном способе изучения ее движения (см. рис. 1.2), то координаты точки равны проекциям на соответствующие оси радиус-вектора точки

,

где   – единичные орты координатных осей.

            Естественный способ. Этот способ используют в тех случаях, когда заранее известна траектория точки. На траектории выбирают неподвижную точку О (начало отсчета), а также положительное и отрицательное направления отсчета расстояний точки от начала отсчета (рис. 1.3). Тогда положение точки М на траектории будет однозначно определяться зависимостью криволинейной координаты S = ОМ от времени

                                                (1.3)

С вязь между координатным и естественным способами определяется выражением

,

где   – первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.

К простейшим движениям твердого тела относятся поступательное и вращательное. Поступательным называется движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному положению. Теорема. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют в каждый момент времени равные скорости и ускорения. Вращательным называется движение твердого тела, при котором все точки некоторой прямой, связанной с телом, остаются неподвижными во время движения. Эта прямая называется осью вращения. Положение тела определено, если задан угол   между плоскостями   и  , проходящими через ось вращения (  с единичным направляющим вектором  ) (рис. 2.2.1) . Плоскость   неподвижна, а плоскость   жестко связана с телом. Угол   измеряется в радианах и изменяется с течением времени,   – уравнение вращательного движения твердого тела. Угловая скорость   характеризует изменение угла поворота с течением времени. Угловое ускорение   – характеризует быстроту изменения угловой скорости.

Если угловая скорость   постоянна, то вращение называется равномерным и происходит по закону  .Если угловое ускорение   постоянно, то вращение называется равнопеременным и происходит согласно уравнениям: ,          .

Модули скорости, ускорения, касательного, нормального ускорений точки вращающегося тела, находящейся на расстоянии   от оси вращения, определяются по формулам: ,  ,  ,  ,  Ускорение точки составляет угол   с направлением нормали, при этом .

Основные понятия и аксиомы динамики Сила – количественная мера механического взаимодействия между телами. Масса – физическая величина, зависящая от количества вещества в теле и являющаяся мерой инертности. Масса является скалярной, положительной, постоянной величиной данного тела. Инертность тела – свойство изменять свою скорость, под действием сил, не скачкообразно, а постепенно и тем медленнее, чем больше количество вещества заключено в данном теле. Материальной точкой будем называть математическое тело, размерами которого, в условиях данной задачи, можно пренебречь (для которого различия в скоростях и ускорениях для отдельной его части, при условии данной задачи можно пренебречь). Аксиомы динамики. Первая аксиома динамики (аксиома инерции).

Эту аксиому также называют законом Галилея-Ньютона, так как впервые ее сформулировал Галилей, а Ньютон включил ее в свой трактат как первый закон. Поэтому ее называют и первым законом Ньютона.

Существуют такие системы отсчета, в которых изолированная материальная точка остается в состоянии покоя или равномерного прямолинейного движения.

Эти системы отсчета и являются инерциальными, а связанные с ними системы координат называют инерциальными системами координат. Вторая аксиома динамики (основная аксиома динамики).

Эту аксиому также называют основным законом механики или вторым законом Ньютона.

В инерциальной системе отсчета ускорение материальной точки пропорционально силе, приложенной к ней: ma=F

Коэффициент пропорциональности m между силой и ускорением называется массой материальной точки. Согласно аксиоме инерции, ускорение точки свободной от действия сил равно нулю. Если к точке приложена сила, она выходит из инерциального состояния, приобретая ускорение a = F / m. Поэтому, чем больше масса, тем меньше ускорение и тем больше способность материальной точки сопротивляться действию силы, тем больше ее инерционность. Иначе говоря, масса характеризует инерционность материальной точки и является ее мерой инерции. Третья аксиома динамики (аксиома действия и противодействия).Эту аксиому также называют третьим законом Ньютона. Две материальные точки взаимодействуют друг с другом с силами, равными по величине, направленными по одной прямой в разные стороны. Третья аксиома динамики относится уже к динамике систем материальных точек и тел. Она позволяет глубже проникнуть в сущность понятия силы. В ней сила представляет не только действие, но и противодействие во взаимодействии, как минимум, двух материальных объектов.

Эта аксиома позволяет отличить реальные силы, возникающие при взаимодействии материальных точек, от фиктивных, которые могут появиться при математических преобразованиях в решении задач механики.

Четвертая аксиома динамики (аксиома независимости действия сил).

Эту аксиому часто называют законом независимости действия сил или принципом суперпозиции.

Под действием нескольких сил материальная точка приобретает ускорение, равное геометрической сумме ускорений, которые бы имела точка под действием каждой силы в отдельности.

Согласно аксиоме, несколько сил (F₁, F₂, ..., F_n), действующих на материальную точку, можно заменить одной силой F = F₁ + F₂ + ... + F_n, то есть она аналогична аксиоме параллелограмма сил в статике.