5.4. Повышение эффективности с помощью «промежуточного вектора».

Вычисление члена уравнения (5.3), соответствующего зеркальному отражению, может оказаться слишком дорогостоящим, поскольку при этом требуется вначале найти вектор r, а затем нормировать его. На практике для ускорения вычислений используется альтернативный член зеркального отражения, который, вероятно, впервые был описан Блинном и используется для ускорения вычислений. Вместо косинуса угла между векторами r и v ищется промежуточный ( halfway ) вектор между s и v, то есть h=s+v, как показано на рис.5.5. Если бы нормаль к поверхности была направлена вдоль вектора h, то наблюдатель увидел бы наиболее яркий зеркальный блик. Поэтому угол между векторами m и h можно использовать для измерения спада интенсивности зеркального отражения, которую видит наблюдатель. Угол не совпадает с углом ( на самом деле угол вдвое больше, чем угол ,если все векторы компланарны; см. упражнения ), однако это различие может быть компенсировано использованием другого значения показателя f. ( Зеркальный член никоим образом не основывается на физических принципах, поэтому по меньшей мере приятно, что такая его коррекция дает приемлемые результаты). Обычно принято при вычислении зеркального члена исходить из , используя при этом скалярное произведение векторов h и m:

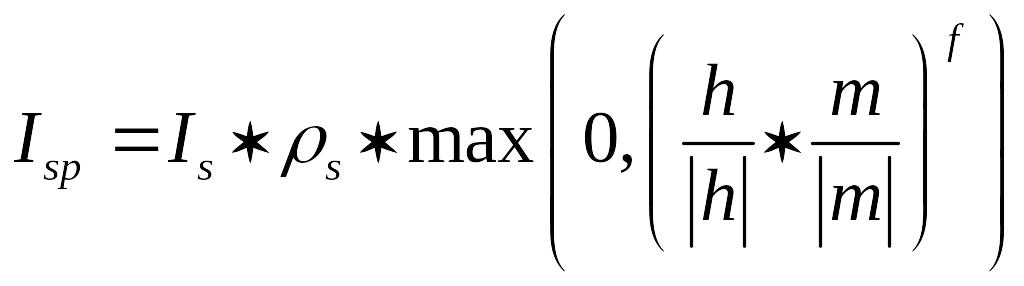(скорректированный зеркальный член). (5.4)

Отметим, что при такой коррекции нет необходимости находить вектор отражения r, что экономит время вычисления. Кроме того, если и источник света, и наблюдатель очень удалены, то векторы s и v одинаковы для различных граней объекта, поэтому вектор b понадобится вычислить всего один раз.

5.5. Фоновые источники и фоновые отражения

Для того, чтобы преодолеть трудности, связанные со сплошными черными тенями, давайте представим себе, что в окружающей среде существует равномерное «свечение фона», называемое фоновым светом (ambient light). Источник фонового свете не располагается в каком-либо определенном месте, и этот свет распространяется во всех направлениях одинаково. Этот источник характеризуется интенсивностью . Каждой грани в данной модели соответствует определенное значение коэффициента фонового отражения (ambient reflection coefficient) (часто он совпадает с коэффициентом диффузного отражения ), а член просто добавляется к тому диффузному и зеркальному свету, который попадает в глаз из каждой точки P на этой грани. Значения и обычно подбираются экспериментально путем варьирования различных величин и выбора наиболее подходящих. Недостаток фонового света делает тени слишком глубокими и резкими, избыток же его делает изображение размытым и мягким.

5.6. Комбинирование компонентов освещения

Теперь мы можем сложить три компонента освещения – диффузный, зеркальный и фоновый, чтобы получить суммарное количество света I, которое попадает в глаз из точки P, а именно:

(5.5)

где введены величины:

(5.6)

Величина I зависит от различных интенсивностей источников и коэффициентов отражения объекта, а также от соотношения положений точки P, глаза и точечного источника света. Здесь интенсивности диффузного и зеркального компонентов обозначены различными буквами, поскольку в OpenGL представляется возможность задавать их раздельно, как мы увидим позднее. На практике обе эти интенсивности обычно имеют одну и ту же величину.

Рассмотрим несколько подробнее изменение интенсивности I в зависимости от положения точки P, для чего снова вернемся к рис. 5.2. Интенсивность I вычисляется для различных точек P рассматриваемой микрограни. Фоновый компонент не претерпевает никаких изменений в пределах микрограни; вектор m одинаков для всех точек P микрограни, но направления векторов s и v зависят от P. (Пусть, например, s=S-P, где S - расположение источника света. Как значение вектора v зависит от точки P и глаза?). Если источник света достаточно удален (это типичный случай), то вектор s при изменении точки P меняется незначительно; так что и диффузный компонент также будет незначительно изменяться для различных точек P. Это особенно верно, когда векторы s и m почти параллельны, так как для малых углов косинус изменяется медленно. Для удаленных источников света изменение направления промежуточного вектора h также слабо зависит от изменения точки P. С другой стороны, если источник света расположен близко к микрограни, то по мере изменения точки P векторы s и h могут сильно изменяться. В этом случае зеркальный компонент может сильно изменяться в пределах микрограни, поэтому яркий блик может быть локализован в ее малой области. Этот эффект усиливается, когда глаз также расположен близко к микрограни, вызывая сильные изменения в направлении v, и когда показатель степени очень f велик.