5.2. Вычисления диффузионной составляющей

Предположим, что свет падает от точечного источника на одну сторону микрограни (faset) поверхности. Какая-то доля света с этой стороны микрограни переизлучается во всех направлениях. А какая-то часть этой переизлучаемой доли достигает глаза с интенсивностью, обозначаемой . Как зависит от направлений m, v и s?

Поскольку рассеяние одинаково во всех направлениях, ориентация микрограни относительно глаза не имеет значения. Поэтому не зависит от угла между векторами m и v (кроме случая v m<0, тогда =0). С другой стороны, количество света, освещающего данную микрогрань, зависит от ориентации микрограни по отношению к источнику света: оно пропорционально «наблюдаемой» источником площади этой микрограни, то есть видимой площади микрограни.

На рис. 5.2 а) в сечении показан точечный источник, освещающий микрогрань S, для случая, когда вектор m параллелен вектору s. На рис.5.2 б) микрогрань отвернута в сторону от источника света на угол . Теперь видимая площадь составляет только долю, равную , от той, что была раньше, так что яркость микрограни S уменьшится во столько же раз. Это соотношение между яркостью и ориентацией поверхности часто называют законом Ламберта (Lambert). Отметим, что для малых углов яркость слабо зависит от угла, поскольку косинус в окрестностях нуля изменяется медленно. Однако при приближении угла к яркость быстро снижается до нуля. Далее, нам известно, что является скалярным произведением ортов s и m. Тогда можно получить следующее выражение для интенсивности диффузного компонента:

где - интенсивность источника света,

- коофициент диффузного отражения (diffuse reflection coefficient). Отметим, что если микрогрань направлена в сторону от глаза, то это скалярное произведение отрицательно, и в этом случае мы принимаем Следовательно, более точная формула для диффузного компонента имеет вид:

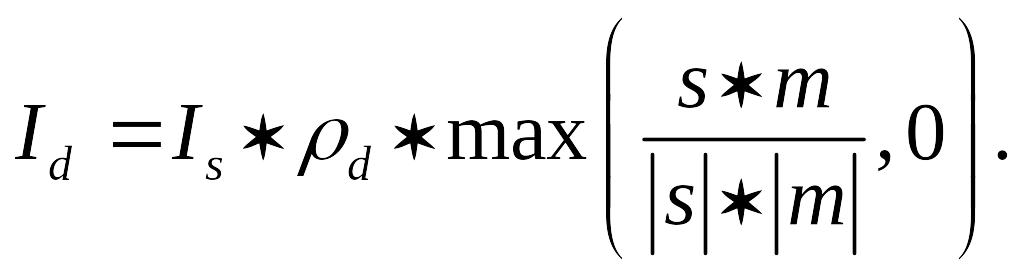(5.1)

5.3. Зеркальное отражение

Реальные объекты не рассеивают свет равномерно во всех направлениях, поэтому к модели закраски добавляется зеркальный компонент. Зеркальное отражение порождает блики, которые могут существенно увеличить реалистичность изображения, заставив объекты блестеть. В данном разделе мы рассмотрим простую модель поведения отраженного света по Фонгу. Эта модель легко реализуется, и OpenGL поддерживает хорошее приближение к ней. Блики, создаваемые отраженным светом по Фонгу, придают объекту вид сделанного из пластмассы, поэтому модель Фонга хороша, когда предназначается для объектов, выполненных из блестящего пластика или стекла. С объектами, имеющими блестящую металлическую поверхность, данная модель работает хуже, однако, как мы увидим, путем тщательного подбора параметров цвета с помощью OpenGL аппроксимация по-прежнему возможна. Разработаны более современные модели отражения света, которые лучше работают с блестящими металлами. На рис. 5.3 а) показана ситуация, в которой свет от источника падает на поверхность и отражается в различных направлениях. Согласно модели Фонга, количество отраженного света имеет наибольшую величину в направлении абсолютного зеркального отражения (вектор r), когда угол отражения равен углу падения. Именно в этом направлении отразился бы весь свет, если бы поверхность была абсолютным зеркалом. При других углах, близких к этому, количество отраженного света быстро убывает, о чем свидетельствуют относительные длины векторов отражения. На рис. 5.3 б) это распределение показано в виде «пучка лучей», известного специалистам по радарам. Расстояние от точки Р до огибающей пучка лучей показывает относительную силу света, рассеянного в данном направлении.

На рис. 5.3, в) показано, как оценить влияние пучка. Направление r полного отражения зависит от вектора s и нормали m к поверхности следующим образом:

(направление зеркального отражения). (5.2)

Для блестящих поверхностей не являющихся абсолютно зеркальными, количество отраженного света убывает с ростом модуля угла между векторами r и v. Истинное количество этого убывания является сложной функцией от , однако в модели Фонга данная зависимость предполагается равной некоторой степени f от косинуса , то есть , где значение f подбирается экспериментально и обычно лежит в пределах от 1 до 200. На рис. 6.4 показан график изменения функции интенсивности в зависимости от угла для различных значений f.

С ростом параметра f отражение становится все более зеркальным и все более концентрируется вдоль направления r. При f= можно было бы смоделировать абсолютное зеркало, однако чистые отражения обычно обрабатывают другим способом.

Используя тот факт, что равен скалярному произведению векторов u и v (после их нормирования), можно смоделировать вклад в зеркальное отражение следующим образом:

, (5.3)

где множитель называется коэффициентом зеркального отражения (specular reflection coefficient). Подобно большинству коэффициентов в модели закрашивания, он обычно определяется экспериментально. (Как и в случае диффузного члена, при отрицательном скалярном произведении r*v значение устанавливается равным нулю.)