
- •Загальні методичні рекомендації
- •Дослідження часових характеристик типових ланок лінійних систем автоматичного управління
- •Порядок виконання роботи
- •Дослідження частотних характеристик типових динамічних ланок
- •Перетворення структурних схем систем автоматичного управління
- •Застосуваня діаграми найквіста і методу кореневого годографа для аналізу систем автоматичного управління
- •Побудова та аналіз діаграми нікольса та діаграми боде
Застосуваня діаграми найквіста і методу кореневого годографа для аналізу систем автоматичного управління
Мета роботи
Провести аналіз стійкості САУ за допомогою діаграми Найквіста та методу кореневого годографу.
Завдання
Навчитись практично застосоаувати діаграму Найквіста та метод кореневого годографу для аналізу стійкості САУ.
Короткі теоретичні відомості
При проведенні аналізу САУ окрім часових і частотних характеристик визначають її стійкість.
Стійкість – це властивість системи повертатись в початкивий сталий режим роботи після виходу з нього в результаті закінчення дії на неї збурення.
Стійкість оцінюють якісно і кількісно. Якісні характеристики: система стійка, система нестійка, система знаходиться на межі стійкості. Кількістно стійкість оцінюють по величині запасу стійкості. Розрізняють запас стійкості по амплітуді і запас стійкості по фазі. Вважають систему стійкою якщо запас стійкості по амплітуді буде більшим або рівним 6 децибелам, а запас стійкості по фазі – більшим або рівним 300.
В самому простому випадку стійкість системи можна визначити по кореням характеристичного рівняння. Характеристичне рівняння представляє собою знаменник передавальної функції, який прирівнюють до нуля. Корені характеристичного рівняння в загальному випадку є комплексними. Тобто, вони складаються з дійсної частини та уявної. Система буде стійкою, якщо дійсні частини усіх коренів рівняння будуть мати від’ємні значення. Наприклад: система буде стійкою, якщо її характеристичне рівняння другого порядку буде мати корені p1= -2+3i та p2= -5-4i. Якщо корені характеристичного рівняння системи представити на комплексній площині, то вони будуть розташовані на лівій її півплощині. Система буде нестійкою, якщо хоч один із коренів характеристичного рівняння буде мати додатну дійсну частину. Наприклад: p1= 5+3i, p2= -5-4i. Система буде знаходитись на межі стійкості у тому випадку, коли один із коренів характеристичного рівняння матиме дійсну частину, що дорівнює нулю. Наприклад: p1= 3i, p2=
-5-4i. Якщо два і більше коренів мають нульові значення дійсних частин, то система буде нестійкою. Наприклад: p1= 3i, p2= -4i .
Стійкість системи визначають і за допомогою інших методів, які не передбачають визначення коренів характеристичного рівняння. Їх називають критеріями стійкості. Для аналізу систем найбільш частіше використовують такі критерії: критерій Рауса-Гурвіца, критерій Найквіста, критерій Михайлова.
Критерій Рауса-Гурвіца може бути сформульованим у формі представленій А. Гурвіцем, так і у формі представленій Е. Раусом.
За Гурвіцем
сисрема з характеристичним рівнянням
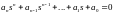 буде стійкою, якщо визначник Гурвіца
і всі його діагональні мінори додатні.
буде стійкою, якщо визначник Гурвіца
і всі його діагональні мінори додатні.
Визначник Гурвіца складається з коєфіціентів характеристичного рівняння:
an-1 an-3 an-5........0
an an-2 an-4…….0
∆n = 0 an-1 an-3…….0
…………………..
..………….. a1 0
0 0 0 a2 a0
Діагональні мінори отримують шляхом викреслювання i-рядка та j-стовбця.
Розглянемо приклад. Необхідно за критерієм Гурвіца визначити стійкість системи третього порядку, яка має характеристичне рівняння:
s3+7 s2+14s+8=0.
Знайдемо значення визначника Гурвіца та діагональних мінорів:
7 8 0
∆3
= 1 14 0 = 720 , ∆1
= 7, ∆2
=
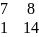 = 90.
= 90.
0 7 8
Отримані значення додатні. Отже, система стійка.
Критерій Рауса базується на упорядкуванні коефіцієнтів характеристичного рівняння. Коефіцієнти рівняння розташовуються такому порядку:
sn |
an an-2 an-4 |
sn-1 |
an-1 an-3 an-5 |
sn-2 |
bn-1 bn-3 bn-5 |
sn-3 |
cn-1 cn-3 cn-5 |
… |
… … … |
s0 |
bn-1 |
де:
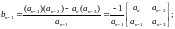
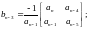
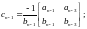
Критерій Рауса формулюється наступним чином: число коренів характеристичного рівняння з позитивною дійсною частиною дорівнює числу змін знака у першому стовпці таблиці Рауса. Тобто, для стійкої САУ у першому стовпці таблиці Рауса не повинно бути змін знака.
Розглянемо САУ 2-го порядку.
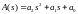 .
.
Таблиця Рауса:
s2 |
a2 a0 |
s1 |
a1 0 |
s0 |
b1 0 |
де:
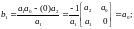
Умова стійкості для САУ 2-го порядку зводиться до умови, щоб всі коефіцієнти характеристичного поліному були позитивними і або негативними.
Розглянемо САУ 3-го порядку.
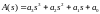 ;
;
Таблиця Рауса:
s3 |
a3 a1 |
s2 |
a2 a0 |
s1 |
b1 0 |
s0 |
c1 0 |
де:

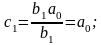
Умова забезпечення стійкості: всі коефіцієнти позитивні; виконання нерівності a2 a1> a0a3.
Якщо a2 a1 = a0a3, тоді САУ знаходиться на межі стійкості і два кореня розташовані на уявній осі.
Критерій Найквіста є частотним методом визначення стійкості систем. У критерії Найквіста розглядається два випадки: перший - коли розімкнена система стійка; другий - коли розімкнена система нестійка.
У випадку коли розімкнена система стійка або знаходиться на межі стійкості критерій Найквіста формулюється наступним чином: замкнена система буде стійкою тоді, коли амплітудно-фазова частотна характеристика розімкненої системи при зміні частоти ω від 0 до + ∞ не охоплює точку з координатами (- 1; j0).
Коли розімкнена система знаходиться на межі стійкості, то її АФЧХ при ω→0 буде прямувати до бескінечності. А це ускладнює процес аналізу. Для того щоб визначитись чи буде амплітудно-фазова частотна характеристика не охоплювати точку з координатами (- 1; j0) необхідно подумки з’єднати уявним півколом проти ходу годинникової стрілки той кінець характеристики, що прямує в безкінечність з додатньою піввіссю дійсної осі комплексної площини. Це правило застосовують і у випадку коли розімкнені системи будуть мати астатизм першого, другого та третього порядку (система має відповідно один, два та три інтегратори). Їх АФЧХ також прямуватимуть до безкінечності.
Для систем, які є нестійкими в розімкненому стані і їх передавальна функція буде мати m полюсів, що розташовані зправа від уявної осі комплексної площини, критерій Найквіста формулюється наступним чином: замкнена система буде стійкою тоді, коли амплітудно-фазова частотна характеристика розімкненої системи при зміні частоти ω від - ∞ до + ∞ охоплює точку з координатами (- 1; j0) m разів.
Критерій Михайлова є графо-аналітичним методом визначення стійкості систем. Він формулюється наступним чином: лінійна система n-го порядку буде стійкою, якщо крива Михайлова охоплює початок координат і поступово проходить n квадрантів. Для того щоб побудувати криву Михайлова необхідно отримати функцію Михайлова. Для цього в поліномі характеристичного рівняння замкненої системи необхідно замінити змінну s на вираз jω, а потім, провести перетворення, виділивши дійсну і уявну частину. Утворений вираз називають функцією Михайлова.
A(s)= ansn + an-1sn-1+ … + a1s + a0 ,
A(jω) = an(jω)n + an-1(jω)n-1 + …+ a1(jω) + a0 = X (ω) + Y(jω) .
Надавши конкретних числових значень частоті, отримаємо X та Y, які будуть визначати кожну точку кривої Михайлова.
За допомогою
кореневого годографа можна не тільки
визначити стійкість системи, але і
проводити її коригування в залежності
від зміни параметрів. В математиці
годографом називають криву лінію, яку
описує якийсь змінний вектор
 .
В теорії автоматичного управління
кореневий годограф – це лінія, що
представляє собою траєкторію зміни
коренів характеристичного рівняння
(полюсів передавальної функції) замкненої
САУ при зміні її визначеного параметру.
.
В теорії автоматичного управління
кореневий годограф – це лінія, що
представляє собою траєкторію зміни
коренів характеристичного рівняння
(полюсів передавальної функції) замкненої
САУ при зміні її визначеного параметру.
Значення
кореня
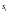 належатиме
кореневому годографу тоді, коли воно
задовольняє амплітудний та кутовий
критерій:
належатиме
кореневому годографу тоді, коли воно
задовольняє амплітудний та кутовий
критерій:
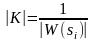 – амплітудний
критерій;
– амплітудний
критерій;
arg W(si) = r(1800), r = ±1, ±3, ±5,… – кутовий критерій,
де W(s) – передаточна функція розімкненої САУ з коефіцієнтом підсилення K.
Властивості кореневого годографу.
1. Кореневий годограф є симетричним відносно дійсної осі комплексної площини.
2.
Кореневий годограф при K=0
бере початок у полюсах функції
W(s),
і при K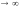 закінчується
у нулях цієї функції, включаючи нулі,
які розташовані у бескінечності.
закінчується
у нулях цієї функції, включаючи нулі,
які розташовані у бескінечності.
3. Якщо передавальна функція розімкненої САУ має α нулів у нескінченності (α≥1), тоді при K кореневий годограф наближається до α асимптот, які розташовані під кутами:
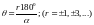
і які перетинатимуть дійсну вісь у точці згідно з рівнням:
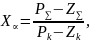
де
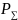 – значення
суми полюсів передавальної функції
розімкненої системи,
– значення
суми полюсів передавальної функції
розімкненої системи,
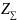 – загальна
сума значень s,
які перетворюють чисельник передавальної
функції в нуль,
Pk
– кількість
полюсів у кінцевих точках годографу,
Zk
–
кількість нулів у кінцевих точках
годографу.
– загальна
сума значень s,
які перетворюють чисельник передавальної
функції в нуль,
Pk
– кількість
полюсів у кінцевих точках годографу,
Zk
–
кількість нулів у кінцевих точках
годографу.
Для деяких α значення кутів нахилу асимптот приведені в табл.2.
Таблиця 2
Кути нахилу асимптот
-
α
Ө, град
0
асимптоти відсутні
1
1800
2
±900
3
±600; 1800
4
±450; ±1350
4. Кореневий годограф включає всі точки на дійсній осі, що розташовані зліва від непарного числа дійсних особливих точок (нулів і полюсів) передавальної функції.
Якщо передавальна функція замкненого контуру містить дійсний нуль або полюс, який знаходиться на дійсній осі, тоді аргумент вектору завжди дорівнюватиме 00 або 1800.
У випадку, коли передавальна функція замкненого контура містить комплексні полюси або нулі, тоді вони завжди утворюють комплексно-спряжені пари. Сума кутів від кожної пари нулів або полюсів до точки на дійсній осі буде завжди дорівнювати 00 або 3600.
5. Кореневий годограф має точоки відриву.
Точки відриву кореневого годографу визначаються коренями рівняння:
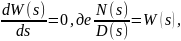
або
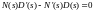
де
 N(s)
– чисельник
передавальної функції розімкненої
системи, D(s)
– знаменник
передавальної функції розімкненої
системи.
N(s)
– чисельник
передавальної функції розімкненої
системи, D(s)
– знаменник
передавальної функції розімкненої
системи.
6.
Кореневий
годограф буде виходити із полюсу
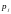 (або
входитиме у нуль
(або
входитиме у нуль
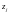 )
під кутами нахилу
)
під кутами нахилу (
(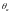 ):
):
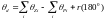 ;
;
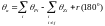 ;
;
де:
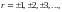
 –
кути
між полюсом
–
кути
між полюсом
 (нулем
(нулем
 )
і полюсом
(
нулем).
)
і полюсом
(
нулем).
Порядок виконання роботи
1. Ознайомитись з можливостями програмних операторів Matlab 6.5: nyquist, real, image, rlocus, rlocfind, residue.
2. Провести дослідження стійкості САУ за допомогою діаграми Найквіста.
Дослідити стійкість САУ з передавальною функцією її розімкненої системи:
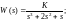
Необхідно спочатку визначити стійкість розімкненої системи будь яким способом, наприклад, за допомогою аналізу коренів характеристичного рівняння або іншим, а потім, стійкість цієї ж системи, тільки уже в замкненому вигляді. Для цього необхідно скористатись критерієм Найквіста та програмними засобами MatLab 6.5:
%K=1
H = tf([1],[1 2 1 0])
nyquist(H); grid
%K=2
H = tf([2],[1 2 1 0])
nyquist(H); grid
%K=3
H = tf([3],[1 2 1 0])
nyquist(H); grid
В результаті реалізації програми необхідно отримати три графіки. Це діаграми Найквіста, які характерні для різних випадків стійкості. Вони отримані шляхом варвіювання коєфіцієнтів у чисельнику заданої передавальної функції. Проведіть аналіз програми і визначте ці коефіцієнти. Проаналізуйте діаграми Найквіста і визначіть випадки, коли САУ є: стійка; нестійка; знаходиться на межі стійкості.
3. Провести дослідження стійкості, застосовуючи діаграму Найквіста, для САУ з ланкою постійної затримки (рис.13).
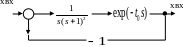
Рис. 13 САУ з ланкою постійної затримки
Для побудови діаграми Найквіста необхідно скористатись наступною програмою MatLab 6.5:
t0=[0.75 0.55 0];
w=0.3:0.1:4;
for k=1:3
[re, im, w]=nyquist([1],[1 2 1 0],w);
re, im
D1=exp(-j*t0(k)*w);
Gw=(re+j*im).*D1;
Greal=real(Gw); Gimag=imag(Gw);
plot(Greal, Gimag)
title('Nyquist Diagram'); xlabel('ReG(jw)');
ylabel('ImG(jw)'); grid; hold on
end
hold off
Проаналізуйте програму. Побудуйте діаграму Найквіста. Визначте за допомогою неї стійкість заданої системи. У тому випадку коли система буде стійкою, варіюючи параметрами передавальної функції, зокрема, ланки з постійною затримкою спробуйте побудувати діаграми Найквіста для випадків, коли САУ є: нестійка; знаходиться на межі стійкості.
4. Дослідити стійкість САУ, якщо передавальна функція її розімкненої системи:
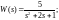

Визначити стійкість розімкненої системи будь яким методом, наприклад, за допомогою аналізу коренів характеристичного рівняння, а потім, стійкість цієї ж системи, тільки вже в замкненому вигляді, скористатись критерієм Найквіста.
Параметр К задати самостійно ( від 1 до 10).
5. Проведення аналізу стійкості САУ за допомогою методу кореневого годографу.
Розглянемо передаточну функцією розімкненої САУ:

Згідно з правилом побудови кореневого годографа (правило №2) графік кореневого годографа розпочинається у полюсах: s = 1, s = - 2, s = - 3 і закінчується у нулях у нескінченості.
Визначимо для кореневого годографа асимптоти з кутами нахилу (правило №3):
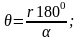 r
=±1,
±3,
…
r
=±1,
±3,
…
Кореневий годограф має три асимптоти з кутами нахилу:± 600; 1800 ( див. табл. № 2, α=3 так як передавальна функція буде прямувати в безкінечність при s = 1, s = - 2, s = - 3 ). Вони перетинають дійсну вісь у точці:
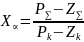

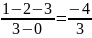 .
.
Згідно з правилом побудови №4 кореневий годограф включає частину дійсної осі у межах інтервалів:
1) -2<s<1 (зліва від першої особливої точки передавальної функції);
2) s<-3; (зліва від третьої особливої точки передаточної функції).
3) s>1 – не містить ніяких особливих точок;
4) -3<s<-2 (розташовано зліва від другої особливої точки передавальної функції, тому ці ділянки не входять до кореневого годографу.
Визначимо точки відриву кореневого годографу (правило №5):
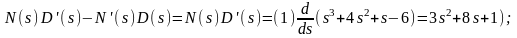 Якщо
отриманий поліном прирівняти до нуля,
то він буде мати такі корені:
Якщо
отриманий поліном прирівняти до нуля,
то він буде мати такі корені:
s = - 2.54 - згідно з правилом №4 ця точка не належить кореневому годографу (ця точка є точкою відриву для тієї частини кореневого годографу, яка відповідає K<0).
s = - 0.132 - ця точка належить кореневому годографу і вона є точкою відриву.
Для визначення діапазону значень K, який забезпечує стійкість САУ, скористаємось критерієм Рауса-Гурвіца:

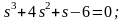
Таблиця 3
Таблиця Рауса
s3 |
1 |
1 |
|
s2 |
4 |
K-6 |
|
s |
(10 – K)/4 |
|
→ K<10 |
s0 |
K-6 |
|
→ K>6 |
САУ є стійкою, якщо: 6<K<10.
Із таблиці Рауса слідує, що при K = 6 замкнена САУ має полюс s = 0.
Визначимо значення K, при якому полюс буде розташовано у початку координат:
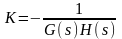 |
S=0=
|
S=0=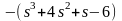 |
S=0
=6;
|
S=0
=6;
При зростанні значень K до K=10 (межа стійкості САУ) критерій Рауса-Гурвіца дає додатній поліном:
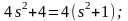
При K = 10 передавальна функція замкненої САУ має полюси: ±j.
| S=j= | S=j =10;
Побудувати кореневий годограф цієї САУ, скориставшись програмним оператором MatLab6.5: rlocus([1],[1 4 1 -6]). Провести аналіз властивостей отриманого кореневого годографа.
6. Побудувати кореневий годограф розімкненої САУ з наступними передавальними функціями:
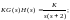
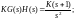
Контрольні питання
1. Дайте означення стійкості САУ.
2. Охарактеризуйте якісні та кількістні показники стійкості САУ.
3. Визначення стійкості по кореням характеристичного рівняння.
4. Критерій стійкості Найквіста.
5. Критерій стійкості Рауса-Гурвіца згідно з Гурвіцем.
6. Критерій стійкості Рауса-Гурвіца згідно з Раусом.
7. Критерій стійкості Михайлова.
8. Визначення кореневого годографу у математиці та в теорії автоматичного управління.
9. Кутовий критерій кореневого годографу.
10. Амплітудний критерій кореневого годографу.
11. Визначення точок відриву кореневого годографу.
6. Побудова кореневого годографу з використанням його властивостей.
Лабораторна робота № 5
