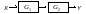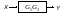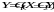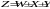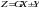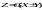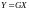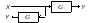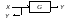Перетворення структурних схем систем автоматичного управління
Мета роботи
Вивчити можливості Matlab 6.5 при визначенні еквівалентних передаточних функцій САУ; вивчити правила перетворення структурних схем САУ; провести перетворення структурних схем САУ за допомогою Matlab 6.5.
Завдання
Провести перетворення структурних схем з послідовним з’єднанням, паралельним з’єднанням, зі зворотнім зв’язком (зустрічно-паралельне з’єднання), схем, перетворення яких проводиться за правилами перенесення вузла і перенесення суматора.
Короткі теоретичні відомості
При перетворенні структурних схем САУ частіше всього застосовують правила: перетворення схем для послідовного з’єднання, паралельного з’єднання, перетворення схем зі зворотнім зв’язком, перенесення вузла і перенесення суматора. Отримання еквівалентних схем за вищезазначеними та іншими правилами наведено в табл.1.
Порядок виконання роботи
Ознайомитись з можливостями програмних операторів Matlab 6.5, що застосовуються для перетворення структурних схем: series; parallel; feedback.
Перетворення структурних схем з послідовним
Таблиця 1
Правила перетворення структурних схем САУ
1. Послідовне з’єднання ланок |
|
|
|
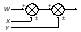
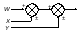
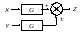
2. Паралельне з’єднання ланок |
|
|
|
3. Охоплення ланки зворотним зв’язком |
|
|
|
4. Перенесення суматорів |
|
|
|
5. Перенесення суматора через ланку проти ходу сигналу |
|
|
|
6. Перенесення суматора через ланку за ходом сигналу |
|
|
|
7. Перенесення вузла через ланку проти ходу сигналу |
|
|
|
8. Перенесення вузла через ланку за ходом сигналу |
|
|
|
з’єднанням .
За допомогою відповідної програми Matlab 6.5 необхідно визначити еквівалентну передавальну функцію Weqv для схеми САУ з послідовним з’єднанням, що представлена на рис.4 . В схемі W1,W2,W3 аперіодичні ланки, параметри яких необхідно задати самостійно (значення kі і Tі можна варіювати від 1 до 10).
.
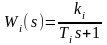Перетворення схеми необхідно проводити послідовно в два етапа: спочатку першу і другу ланку, а потім, отриману еквівалентну ланку W12 з трейтьою ланкою W3.
Рис.4 Схема з послідовним з’єднанням
При перетворенні схем з послідовним з’єднанням передаточні функції перемножаються:
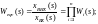
3. Перетворення структурних схем з паралельним з’єднанням.
За допомогою програми Matlab 6.5 необхідно визначити еквівалентну передавальну функцію для схеми САУ з паралельним з’єднанням, що представлена на рис.5 . В схемі W1,W2,W3 аперіодичні ланки, параметри яких необхідно задати самостійно. Перетворення схеми необхідно проводити послідовно в два етапа: спочатку першу і другу ланку, а потім, отриману еквівалентну ланку W12 з третьою ланкою W3 .
При перетворенні схем з послідовним з’єднанням передаточні функції додаютьсяються:
Рис.5 Схема з паралельним з’єднанням
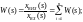
4. Перетворення структурних схем зі зворотнім зв’язком (зустрічно-паралельне з’єднання ланок) .
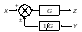
За допомогою програми Matlab 6.5 необхідно визначити еквівалентну передаточну функцію для схеми САУ зі зворотнім зв’язком, що представлена на рис.6.
В схемі W1,W2 аперіодичні ланки, параметри яких необхідно задати самостійно.
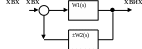
Рис.6 Схема зі зворотнім зв’язком
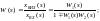
При перетворенні структурних схем зі зворотнім зв’язком в знаменнику еквівалентної передаточної функції буде фігурувати знак “+”, якщо зворотній зв’язок від’ємний і навпаки.
5. Перетворення структурних схем з використанням правил перенесення точки розгалудження та перенесення сумматора.
Розглянемо структурну схему системи управління, яку представлено на рис.7 та поступово проведемо її перетворення.
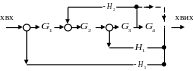
Рис.7 Структурна схема для перетворення з використанням правил перенесення точки розгалудження та перенесення сумматора
;
;
;
;
;
;
.
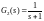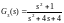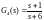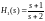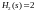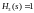Еквівалентну передавальну функцію цієї САУ можна визначити за допомогою програми Matlab:
ng1=[1]; dg1=[1 10]; sysg1=tf(ng1,dg1);
ng2=[1]; dg2=[1 1]; sysg2=tf(ng2,dg2);
ng3=[1 0 1]; dg3=[1 4 4]; sysg3=tf(ng3,dg3);
ng4=[1 1]; dg4=[1 6]; sysg4=tf(ng4,dg4);
nh1=[1 1]; dh1=[1 2]; sysh1=tf(nh1,dh1);
nh2=[2]; dh2=[1]; sysh2=tf(nh2,dh2);
nh3=[1]; dh3=[1]; sysh3=tf(nh3,dh3);
sys1=sysh2/sysg4;
sys2=series(sysg3,sysg4);
sys3=feedback(sys2,sysh1,+1);
sys4=series(sysg2,sys3);
sys5=feedback(sys4,sys1);
sys6=series(sysg1,sys5);
sys=feedback(sys6,[1])
Пояснення:
1-ий крок – представленя передавальних функцій ланок у вигляді, необхідному для програмування (перші 7 рядків: для передаточнох функцій G1,G2,G3,G4 - перших чотири рядки, для H1,H2,H3 - наступні три);
2-ий крок –
переміщення точки розгалуження сигналу
через ланку
.
При цьому змінюється передавальна
функція ланки
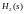(див. правила перетворення структурних
схем САУ).
sys1=sysh2/sysg4;
3-ій крок –
визначення еквівалентної передавальної
функції: передавальнана функція прямого
шляху – послідовне з’єднання ланок
;
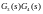передавальна функція зворотного з’язку
-
(див. правила перетворення структурних
схем САУ);
sys2=series(sysg3,sysg4);
sys3=feedback(sys2,sysh1,+1);
4-ий крок -
визначення еквівалентної передавальної
функції: передавальна функція прямого
шляху - послідовне з’єднання ланки
з еквівалентною передавальною функцією,
яка була визначена на 3-му кроці;
передавальна функція зворотнього
з’язку -
(див. правила
перетворення структурних схем САУ);
sys4=series(sysg2,sys3);
sys5=feedback(sys4,sys1);
5-ий крок –
визначення еквівалентної передавальної
функції: передавальна функція прямого
шляху - послідовне з’єднання ланки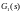
з еквівалентною передавальною функцією,
яка була визначена на 4-му кроці;
передавальна функція зворотнього
з’язку -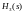
Еквівалентна передаточна функція:
Transfer function:
s^5 + 4 s^4 + 6 s^3 + 6 s^2 + 5 s + 2
-------------------------------------------------------------------------- .
12 s^6 + 205 s^5 + 1066 s^4 + 2517 s^3 + 3128 s^2 + 2196 s + 712
6. Перетворення структурних схем з використанням правил перенесення перенесення суматора.
Розглянемо структурну схему системи управління, яку представлено на рис.8. та поступово проведемо її перетворення.
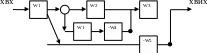Рис.8
Структурна схема для перетворення з
використанням правил перенесення
суматора
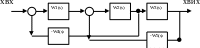
Рис.9 Структурна схема після першого кроку перетворення, в якій здійснено перенесення другого суматора проти ходу сисналу
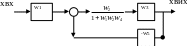
Рис.10 Структурна схема після другого кроку перетворення, в якій спростили внутрішній контур зі зворотнім зв’язком
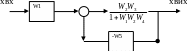
Рис.11 Структурна схема після третього кроку перетворення, в якій спростили головну гілку схеми з використанням правила для схем з послідовним з’єднанням
Рис.12. Структурна схема на заключному кроці перетворення
з послідовним з’єднанням
Врезультаті перетворень загальна формула передавальної функції для вихідної схеми (рис.8) буде мати вигляд:
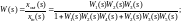
За допомогою відповідних програм Matlab 6.5 необхідно визначити еквівалентну передавальну функцію САУ, що представлена на рис.8. В якості передавальних функцій необнідно взяти наступні :
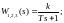
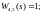
Значення
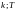кожний студент обирає самостійно (від
1 до 10).
Контрольні питання
1. Які є типи з’єднання ланок?
2. Як проводиться перетворення схем з паралельним зв’язоком ланок?
3. Як проводиться перетворення схем з зустрічно-паралельним зв’язком ланок?
4. Як проводиться перетворення схем з послідовним зв’язоком ланок?
5. Сформулюйте правила перенесення суматора.
6. Сформулюйте правила перенесення точки розгалуження.
7. Які використовуються програми Matlab 6.5 для визначення еквівалентної структурної схеми САУ?
8. Сформулюйте правила визначення передавальних функцій відносно сигналів управління та збурення.
Лабораторна робота №4