
- •Загальні методичні рекомендації
- •Дослідження часових характеристик типових ланок лінійних систем автоматичного управління
- •Порядок виконання роботи
- •Дослідження частотних характеристик типових динамічних ланок
- •Перетворення структурних схем систем автоматичного управління
- •Застосуваня діаграми найквіста і методу кореневого годографа для аналізу систем автоматичного управління
- •Побудова та аналіз діаграми нікольса та діаграми боде
Дослідження частотних характеристик типових динамічних ланок
Мета роботи
Вивчити можливості лінійного аналізу САУ за допомогою Simulink; провести дослідження частотних характеристик типових динамічних ланок.
Завдання
Побудувати амплітудно-частотні характеристики (АЧХ), фазо-частотні характеристики (ФЧХ) типових динамічних ланок, провести дослідження цих характеристик в залежності від зміни параметрів.
Короткі теоретичні відомості
При проведенні аналізу динамічних характеристик САУ важливе значення мають не тільки часові характеристики (перехідна та імпульсна), але і частотні.
Частотні характеристики описують сталі вимушені коливання на виході ланки, які виникають в наслідок подачі гармонійного сигналу на вхід ланки. Вхідний і вихідний сигнал описують відповідно формулами
х(t)= Авх sinωt,
y(t)= Авих sin(ωt + φ),
де φ - зсув по фазі, ω- циклічна частота, t – час, Авх , Авих –амплітуда вхідного та вихідного сигналу.
Функції, що мають залежність амплітуди або фази вихідного сигналу відносно частоти вхідного сигналу називаються частотними характеристиками (ЧХ). Аналіз ЧХ системи з метою дослідження її динамічних властивостей називається частотним аналізом.
Залежність відношеня амплітуд вихідного сигналу до вхідного (А=Авих/Авх) від частоти ω називають амплітудною частотною характеристикою (АЧХ).
Залежність зміни величини зсуву фази вихідного сигналу по відношенню до вхідного від частоти називають фазовою частотною характеристикою (ФЧХ).
Якщо функціонально об’єднати фазову і амплітудну характеристики, то утвориться амплітудно-фазова частотна характеристика. Вона може бути побудована в полярних координатах та в декартових.
Амплітудна і фазова частотна характеристики можуть бути представлені за допомогою логарифмічних коодинат. Логарифмічна амплітудна частотна характеристика (ЛАЧХ) будується в залежності 20 lg A від lg ω (де А= Авих/Авх- відносна амплітуда), а логарифмічна фазова характеристика представляє собою залежність φ від lg ω.
Амплітудна і фазова частотна характеристики можуть бути отримані не тільки за допомогою гармонійного сигналу, але і аналітично шляхом заміни в передаточній функції значення s на jω:
W(jω)=A(ω)ejφ(ω)=P(ω)+jQ(ω),
де Р(ω) - дійсна ЧХ (ДЧХ); Q(ω) – уявна ЧХ (УЧХ); А(ω)- амплітудна ЧХ (АЧХ): φ(ω)- фазова ЧХ (ФЧХ). АЧХ визначають по формулі:
A2(ω) = P2(ω)+Q2(ω).
ФЧХ визначають по формулі:
φ(ω) = arctg (Q(ω)/ P(ω)).
Порядок виконання роботи
1. Ознайомлення з деякими функціональними можливостями лінійного аналізу Simulink (Linear analysis).
Розглянемо порядок побудови деяких функцій лінійного аналізу.
1.1 Відкрити вікно Matlab 6.5.
1.2 Натиснути піктограму Simulink. Повинно з’явитись вікно Simulink Library Browser.
1.3 У вікні Simulink Library Browser натиснути піктограму File.
1.4 Натиснути піктограму Continuous.
1.5 Перенести піктограму Transfer Fcn на біле поле вікна untitled і внести інформацію для передавальних функцій:
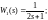
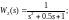
1.6 Натиснути піктограму Tools у вікні untitled.
1.7 Натиснути піктограму Linear analysis.
1.8 Перенести
піктограми Input
Point і
Output Point на
біле поле вікна untitled
і зробити відповідне з’єднання зліва
і справа відносно передавальної функції
(Transfer Fcn)
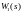 .
.
1.9 Натиснути піктограму Edit у вікні LTI Viewer: untitled.
1.10 Натиснути піктограму Plot configurations.
1.11 Обрати квадрат з 6 прямокутниками.
1.12 Обрати наступні функції у секції Response type: Bode, Nyquist, Nichols, Pole/Zero, Step, Impulse, (кожен раз необхідно підтвердити свій вибір).
1.13 Натиснути піктограму Simulink.
1.14 Натиснути піктограму Get Linearized Model.
Після побудови
функцій:
Bode, Nyquist, Nichols, Pole/Zero, Step, Impulse
для
необхідно провести побудову їх для
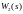 у
тій же самій послідовності.
у
тій же самій послідовності.
2. Визначення амплитудно-частотних характеристик (АЧХ) для ланок першого та другого порядку.
Проведемо побудову амплитудно-частотних характеристик для ланок першого та другого порядків за допомогою відповідних програм Matlab.
2.1 Розглянемо АЧХ аперіодичної ланки першого порядку:
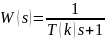
Надати функції Т(k), що фігурує у вищезазначеній формулі, значеня 1, 2, 3, 4. Для кожного із зазначених значень Т(k) необхідно побудувати за допомогою програми Matlab залежність відносної амплітуди від частоти.
w=0:0.05:3;
T=[1 2 3 4];
for k=1:4
Gnum=[0 1];
Gden=[T(k) 1];
Gjomega=
freqs(Gnum,Gden,w)
Gmag=abs(Gjomega)
plot(w,Gmag)
title('Gain Frequency Response of G(s)')
xlabel('Omega')
ylabel('G(j*omega)')
grid on
hold on
end
hold off
Необхідно провести аналіз побудованих АЧХ, зазначивши яка спостерігається закономірність зміни їх при збільшенні значення постійної часу Т(k).
2.2 Розглянемо АЧХ коливальної ланки:
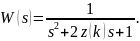
Надати функції z(k), що фігурує у вищезазначеній формулі, значеня 0.25, 0.5, 0.707, 0.9. Для кожного із значень z(k) побудувати за допомогою програми Matlab залежність відносної амплітуди від частоти.
w=0:0.05:3;
z=[0.25 0.5 0.707 0.9];
for k=1:4
Gnum=[0 0 1];
Gden=[1 2*z(k) 1];
Gjomega=freqs(Gnum, Gden, w);
Gmag=abs(Gjomega);
plot(w, Gmag);
title('Gain Frequency Response of G(s)')
xlabel('Omega')
ylabel('G(j*omega)')
grid on
hold on
end
hold off
Необхідно провести аналіз побудованих АЧХ, зазначивши яка спостерігається тенденція зміни їх при збільшенні значення коефіцієнта затухання z(k) .
2.3 Розглянемо АЧХ аперіодичної ланки другогого порядку:
Надати функції z(k) значеня 1, 1.25, 1.5, 1.75, 2. Для кожного із значень z(k) побудувати за допомогою програми Matlab залежність відносної амплітуди від частоти.
w=0:0.05:3;
z=[1 1.25 1.5 1.75 2];
for k=1:4
Gnum=[0 0 1];
Gden=[1 2*z(k) 1];
Gjomega=freqs(Gnum, Gden, w);
Gmag=abs(Gjomega);
plot(w, Gmag);
title('Gain Frequency Response of G(s)')
xlabel('Omega')
ylabel('G(j*omega)')
grid on
hold on
end
hold off
Необхідно провести аналіз побудованих АЧХ, зазначивши яка спостерігається закономірність зміни їх при збільшенні значення коефіцієнта затухання z(k) .
Скориставшись пунктами 2.1-2.3, побудуйте АЧХ інтегрувальної та диференціювальної ланок.
2.4 Розглянемо ФЧХ аперіодичної ланки першого порядку:
Побудувати фазо-частотні характеристики для аперіодичної ланки першого порядку за допомогою програми Matlab.
Matlab script:
w=0:0.1:3;
t=[1 2 3 4];
for k=1:4
x=w*t(k);
phi=-atan(x)
y=phi*180/pi;
title('Phase Frequency Response')
xlabel('Omega')
ylabel('Phase angle')
plot(w, y);
grid on
hold on
end
hold off
Необхідно провести аналіз побудованих ФЧХ та зробити відповідні висновки.
2.5 Розглянемо ФЧХ аперіодичної ланки другого порядку:
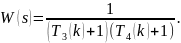
Побудувати графіки, в яких T3(k) та T4(k) відповідно дорівнюють значенням 2, 3, 4, 5 та 1, 2, 3, 4.
Програма для побудови ФЧХ :
w=0:0.1:6;
for k=1:4
t3=[2 3 4 5];
t4=[1 2 3 4];
x1=w*t3(k);
x2=w*t4(k);
phi=-atan(x1)-atan(x2)
y=phi*180/pi;
plot(w,y)
title('Phase Frequency Response')
xlabel('Omega')
ylabel('Phase angle')
grid on
hold on
end
hold off
Необхідно провести аналіз побудованих ФЧХ та зробити висновки.
2.6 Розглянемо ФЧХ коливальної ланки:
Для кращої
деталізації ФЧХ коливальної ланки
необхідно виконати побудову графіків
для одних і тих самих функцій спочатку
від 0 до
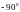 ,
а потім, від
до
,
а потім, від
до
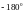 .
.
Від 0 до :
w=0:0.1:1
t=1;
zeta=0.7;
a=(2*zeta*w*t)./(1-w.^2*t.^2);
alpha=-atan(a)
x=alpha*180/pi;
plot(w,x,'r')
title('Phase Frequency Response, zeta=0.7')
xlabel('Omega')
ylabel('Phase angle')
grid on
Від до :
w=1.1:0.1:6
t=1;
zeta=0.7;
a=(2*zeta*w*t)./(1-w.^2*t.^2);
alpha=-atan(a)
y=-alpha*180/pi;
x=-y-180;
plot(w,x,'b')
title('Phase Frequency Response, zeta=0.7')
xlabel('Omega')
ylabel('Phase angle')
grid on
Після побудови графіків АЧХ і ФЧХ необхідно проаналізувати їх.
Скориставшись пунктами 2.4-2.6, по аналогії побудуйте ФЧХ інтегрувальної та диференціювальної ланок.
Контрольні питання
1. Яку характеристику САУ називають частотною?
2. Які бувають чатотні характеристики? Назвіть їх.
3. Дайте означення амплітудно-частотній характеристиці.
4. Дайте означення фазо-частотній характеристиці.
5. Дайте означення амплітудно-фазовій частотній характеристиці.
6. Яким чином можна отримати частотні характеристики?
7. Поняття частотної передаточної функції.
8. Поняття логарифмічної амплітудно-частотної характеристики.
9. Поняття логарифмічної фазово-частотної характеристики.
10. Часові і частотні характеристики безінерційної ланки.
11. Часові і частотні характеристики аперіодичної ланки першого порядку.
12. Часові і частотні характеристики коливальної ланки.
Лабораторна робота №3
