12.1 Применение метода площадей для анализа динамической устойчивости простых систем

Метод площадей удобен для анализа динамической устойчивости системы вида "генератор - внешняя схема - ШБМ" при разовых резких изменениях в схеме или режиме. На рис. 12.2 показан пример анализа динамической устойчивости схемы при аварии: I - доаварийный режим, II - аварийный режим.

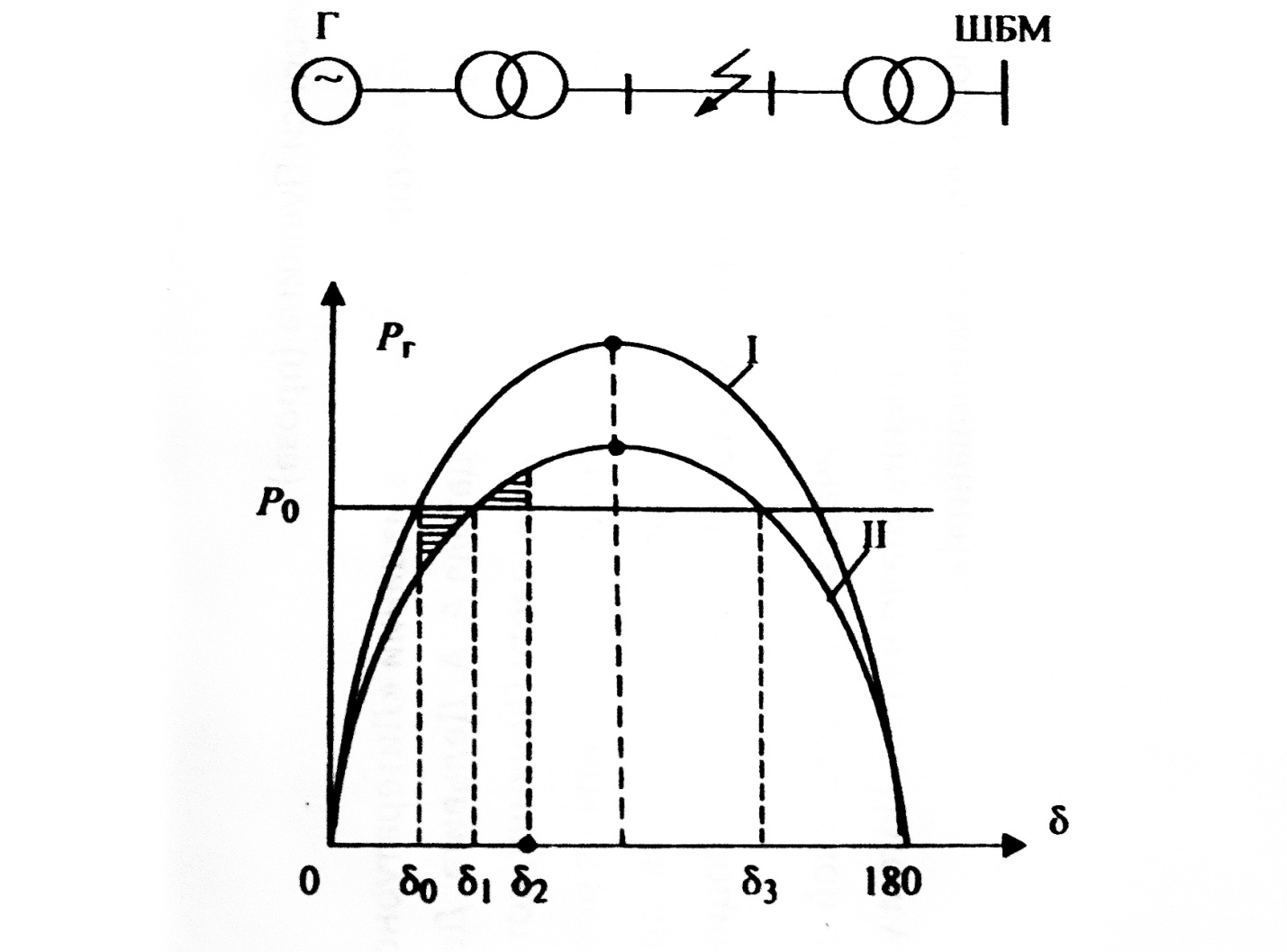
Рис. 12.2

Здесь площадка ускорения

Площадка торможения

Возможная площадка торможения

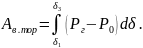
Генератор динамически устойчив, если возможная площадка торможения больше площадки ускорения. Если всей возможной площадки не хватает для компенсации площадки ускорения или если площадка торможения отсутствует (максимум аварийной угловой характеристики лежит ниже прямой , характеризующей мощность, отдаваемую генератору турбиной), то генератор динамически неустойчив.

Метод площадей применим для анализа динамической устойчивости и при сложном ходе аварий, если заранее известно, при каких значениях углов осуществляется тот или иной переход. В этом случае вывод об устойчивости или неустойчивости делается на основе сравнения результирующих площадок ускорения и торможения. Пример расчета динамической устойчивости методом площадей показан ниже.

Пример 12.1. Необходимо определить, устойчив ли динамически генератор при возникновении в точке К металлического однофазного КЗ в системе, представленной на рис. 12.3.

Параметры элементов системы:

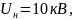
генератор Г: АРВ отсутствует, соединение обмоток - "звезда с заземленной нейтралью",

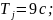
трансформатор T1: 12%, конструкция - 3 однофазных, соединение обмоток (НН-ВН) - ???;

трансформатор T2: 12%, конструкция - трехфазный пятистержневой, соединение обмоток - ???;

линия Л:

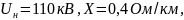
система C: соединение ???;

Передаваемая в приемную систему мощность S=40+j9 МВ .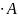

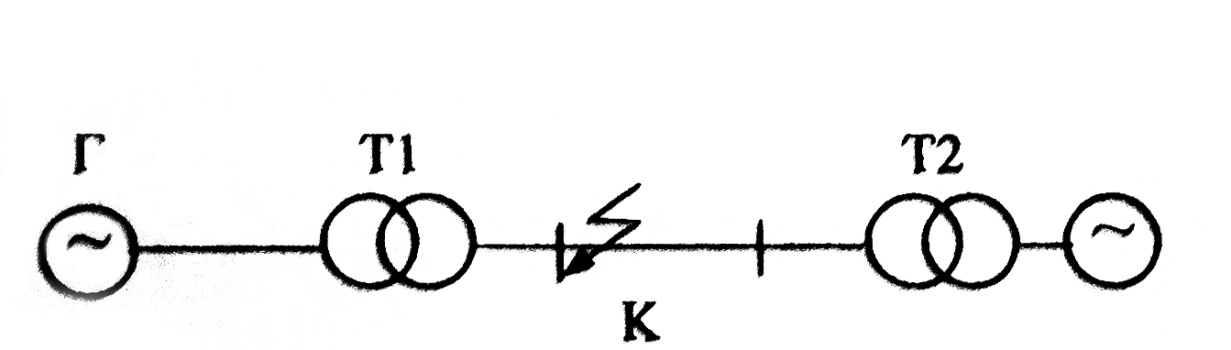
Рис. 12.3

Решение

За базисные условия примем ???виях определим параметры элементов системы в относительных ??? доаварийном режиме.

1. Генератор Г (при расчетах динамической устойчи??? переходными параметрами):

2. Трансформаторы Т1, Т2:

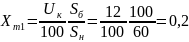
3. Линия Л:

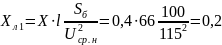
Полное сопротивление доаварийной схемы замещ??? рис. 12.4:

Рис. 12.4

Находим ток на приемных шинах в относительных е??? счета принят вектор напряжения приемной системы):

ЭДС генератора в схеме замещения:,

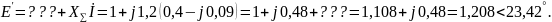
До аварийная угловая характеристика

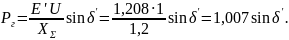
В аварийном режиме схема прямой последовательности показана на рис. 12.5, где

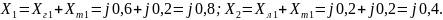
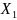
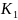
E ’ 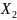U

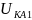
Рис. 12.5

Схема обратной последовательности показана на рис. 12.6.

Рис. 12.6

По схеме рис. 12.6 определим результирующее сопротивление

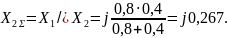
Схема нулевой последовательности показана на рис. 12.7. Эта схема включает в себя только повышающий трансформатор Т1, так как в сторону

понижающего трансформатора Т2 ток нулевой последовательности течь не может (со стороны КЗ нет заземления нейтрали).

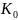
Рис. 12.7

Таким образом, результирующее сопротивление будет

Сопротивление шунта для однофазного КЗ

Схема для расчета аварийной угловой характеристики показана на рис. 12.8.

E’ U

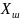
Рис. 12.8

По схеме рис. 12.8 определим взаимное сопротивление

Аварийная угловая характеристика

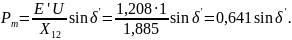
Построив Ι – до аварийную и ΙΙ – аварийную угловые характеристики, определяем величины площади ускорения и возможной площади торможения (рис. 12.9).

Генератор устойчив, так как использует только часть возможной площади торможения. В результате переходного процесса он (после того, как качания углов затухнут) остается работать на аварийной угловой характеристике с углом

12.2. Применение метода последовательных интервалов для анализа динамической устойчивости простых систем

Метод последовательных интервалов применятся для анализа динамической устойчивости при любом ходе аварии, когда динамические переходы известны только как функции времени.

Если у генераторов нет АРВ, а также не учитываются электромагнитные переходные процессы в обмотке возбуждения генератора, то принимается допущение, что ЭДС E’ остается неизменной в течение рассматриваемого момента времени, и приближенно решается в конечных приращениях нелинейное дифференциальное уравнение движения машины:

где - синхронная скорость.

Применительно к системе «генератор - внешняя сеть - ШБМ» порядок расчета следующий.

1. Для заданной системы составляют схему замещения. Определяют ее параметры в относительных единицах. Рассчитывают до аварийную угловую характеристику.

2.Для всех аварийных состояний схемы определяют сопротивление шунтов (дополнительные сопротивления). С их учетом находят значения результирующих параметров и рассчитывают аварийные угловые характеристики.

3.Аналогичные расчеты угловых характеристик производят также для других изменений в схеме, предусмотренных ходом аварии.

4.Разбивают время на интервалы ∆t (обычно ∆t =0,01÷0,05 с). Определяют постоянную интегрирования

где ƒ – частота системы, Гц; 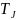- постоянная инерции генератора, с.

5. Для первого момента времени аварии определяют величину небаланса мощности на валу генератора ∆ . Находят приращение угла на первом интервале

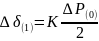
и значение угла в его конце

6.С учетом определяют небаланс мощности на валу генератора в конце первого (начале второго) интервала времени . Находят приращение угла на втором интервале

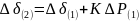
и угол в конце второго интервала

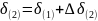и так далее.

На всех последующих интервалах приращение угла определяют по формуле

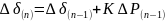(12.1)

Вплоть до очередного резкого изменения режима. На первом интервале после такого изменения приращения угла определяют по формуле

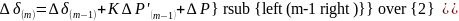
где - избыток мощности на валу генератора, определяемой угловой характеристикой, с которой осуществляется переход; - избыток мощности на валу генератора, определяемой угловой характеристикой, на которую осуществляется переход.

Дальше снова используется формула (12.1) до очередного резкого изменения состояния системы. Расчет ведут до тех пор, пока не будут получены исчерпывающие сведения об устойчивости или неустойчивости генератора. Признаком устойчивости является начавшееся уменьшение угла δ. Если же угол δ непрерывно увеличивается, то это говорит о неустойчивости генератора.

Пример расчета динамической устойчивости простой системы методом последовательных интервалов, при принятии допущения, что показан ниже.

При наличии у генератора АРВ методом последовательных интервалов решаются совместно уравнение движения генератора, уравнение электромагнитного переходного процесса в обмотке возбуждения генератора и уравнение, описывающее закон изменения тока возбуждения при действии канала форсировки АРВ. Данные уравнения и алгоритм расчета показаны в примере 12.3, где расчет проводится с помощью ЭВМ.

Пример 12.2. Для ранее рассмотренной системы (рис. 12.2) определить, устойчив ли динамически генератор при ходе аварии: на линии происходит двухфазное КЗ на землю, через 0,1 с поврежденная линия отключается с двух сторон, а затем через 0,25 с происходит АПВ.

Решение

До аварийная схема замещения соответствует рис. 12.4. Для нее 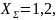E’=1,208, =0,4.

Характеристика

Схема прямой последовательности соответствует рис. 12.5, где 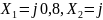0,4. Схема обратной последовательности соответствует рис. 12.6. Для нее Схема нулевой последовательности соответствует рис. 12.7. Для нее

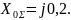
Сопротивление шунта для двухфазного КЗ на землю

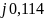
Схема для расчета угловой характеристики при двухфазном КЗ на землю соответствует рис. 12.8. Тогда

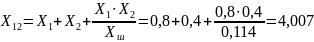
,и угловая характеристика имеет вид

Для случая отключения аварийной линии угловая характеристика

Отсутствует ( = 0), так как при этом прерывается связь между передающим

Генератором и приемником. Примем за основу интервал =0,05 с. Тогда при расчете угла ’ в градусах и времени в секундах постоянная интегрирования будет:

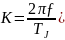
Расчет переходного процесса:

1. Первый интервал (после наступления КЗ):

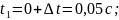
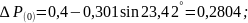
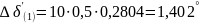
2. Второй интервал (продолжается режим КЗ):

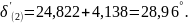
3. Третий интервал (первый интервал после отключения аварийной линии):

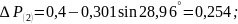
256

;

4. Четвертый интервал (продолжается режим отключения линии):

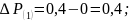
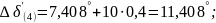
5. Пятый интервал (продолжается режим отключения линии):

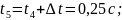
6. Шестой интервал (продолжается режим отключения линии):

7. Седьмой интервал (продолжается режим отключения линии):

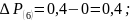
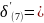10 .

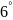8. Восьмой интервал (первый интервал после успешного АПВ):

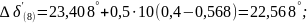
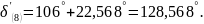
9. Девятый интервал:

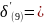147,26 .

10. Десятый интервал:

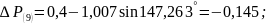
11. Одиннадцатый интервал:

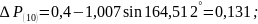
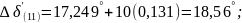
Вывод: генератор неустойчив, так как угол беспредельно растет во времени.

Пример 12.3. Станция работает через линию электропередачи на шины бесконечной мощности (рис. 12.10). Требуется определить предельное время отключения КЗ при учете реакции якоря и действии форсировки возбуждения, если в точке К произошло двухфазное КЗ на землю. Параметры схемы замещения системы в относительных единицах, приведенные к базисным условиям, равны:

Генератор трансформаторы

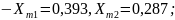
линия

Параметры режима в относительных единицах равны:

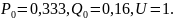
Коэффициент форсировки возбуждени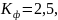я постоянная времени обмотки возбуждения возбудителя