9.4 Влияние конденсаторных батарей на устойчивость узла нагрузки

Установка конденсаторных батарей в узлах нагрузки в целях улучшение экономических показателей распределительной сети может сказаться на устойчивости двигателей. В этом случае для определения статистической устойчивости узла нагрузки можно воспользоваться практическими критериями, которые используются для анализа статистической устойчивости комплексной нагрузки.

Пример расчета статистической устойчивости узла нагрузки при наличии батарей конденсаторов показан ниже.

Пример 9.7. На рис. 9.19 изображена схема, где нагрузка, представлен­а в виде эквивалентного АД, получает питание от станции Г через транс­форматоры Т1, Т2 и линию электропередачи Л. Схема замещения исследуе­мой системы представлена на рис. 9.20. Параметры схемы замещения в отно­сительных единицах следующие: сопротивление эквивалентного генератора 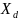=0,2; суммарное сопротивление трансформаторов Т1, Т2 и линии Л 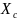= 0,3; суммарное сопротивление рассеяния двигателя Х_s =0,01; сопротив­ление ветви намагничивания АД 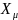=3,5. Напряжение на шинах нагрузки 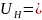1, при этом мощность, потребляемая механизмом АД, = 1.

Требуется выяснить влияние компенсации реактивной мощности на­грузки с помощью батарей конденсаторов (БК) на устойчивость узла нагруз­ки. Для этого следует рассмотреть два режима: когда БК отключены и когда БК включены для получения коэффициента мощности 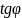=0,2.

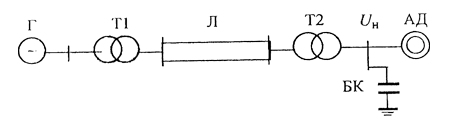
Рис. 9.19

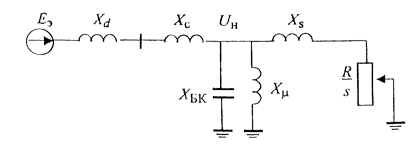
Рис. 9.20

Решение

Расчет состоит из двух этапов.

1. Расчет статической устойчивости узла нагрузки при наличии БК в узле нагрузки.

Вначале определим скольжение , с каким работал двигатель при из уравнения

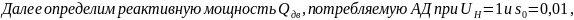
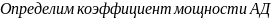
Определим необходимую мощность БК , чтобы коэффициент мощности

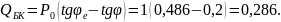
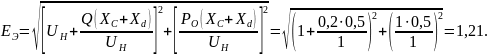
Задаемся напряжением на шинах нагрузки

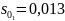Далее определим при и

Найдем реактивную мощность, выдаваемую БК при :

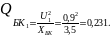
Определим реактивную мощность, поступающую в узел нагрузки:

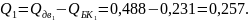
Затем определим 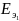при

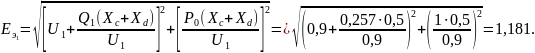
Далее задаемся другими значениями напряжения U на шинах нагрузки и при каждом значении U аналогично определим Результаты расчета приведены в табл. 9.2.

Таблица 9.2

1,0	0,01	0,486	0,286	0,2	1,21
0,9	0,013	0,488	0,231	0,257	1,181
0,8	0,0175	0,532	0,183	0,349	1,19
0,7	0,0259	0,658	0,14	0,518	1,286

По результатам расчета, представленным в табл. 9.2, построим зависимость (рис. 9.21) и по ней, пользуясь критерием dE/dU=0, определим и критическое напряжение

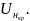
2. Расчет статической устойчивости нагрузки при отсутствии БК в узле нагрузки.

Задаемся различными значениями напряжения U в узле нагрузки и при каждом значении U определяем 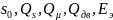. Результаты расчета приведены в табл. 9.3.

Таблица 9.3

1,0	0,01	0,2	0,286	0,486	1,34
0,9	0,013	0,257	0,231	0,488	1,296
0,8	0,0175	0,349	0,183	0,532	1,293
0,7	0,0259	0,518	0,14	0,658	1,37

По результатам расчета, представленным в табл. 9.3, построим зависимость 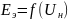(рис. 9.21: 1 - при наличии БК в узле нагрузки; 2 - при отсутствии БК в узле нагрузки).

Коэффициенты запаса устойчивости нагрузки:

при наличии БК:

при отсутствии БК

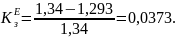
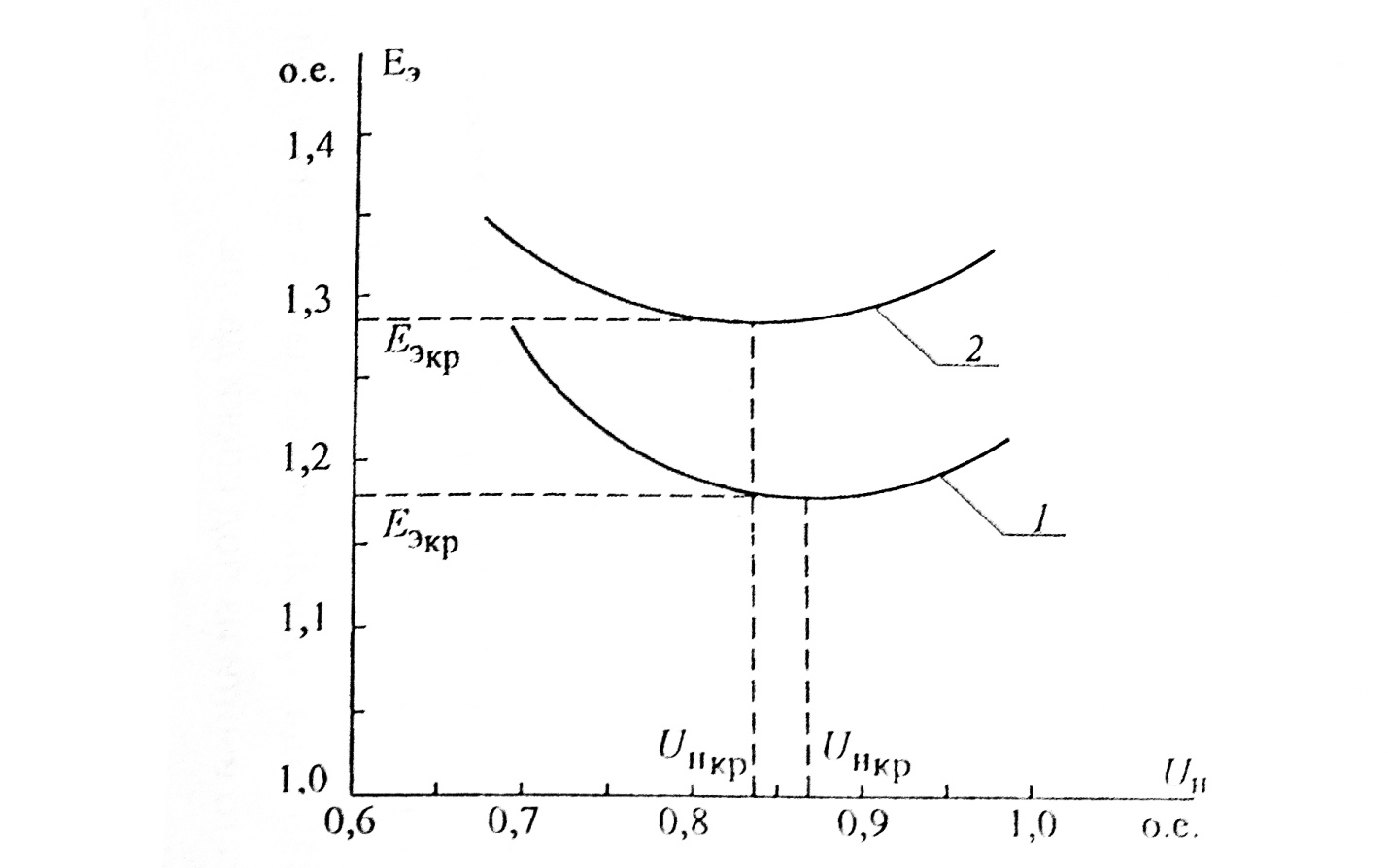
Рис. 9.21

Вывод. Наличие БК в узле нагрузки ухудшает статическую устойчивость.