
- •Глава 9. Определение статической устойчивости
- •9.1 Определение статической устойчивости асинхронного двигателя
- •9.2 Определение статической устойчивости синхронного двигателя
- •9.3 Определение статической устойчивости комплексной нагрузки
- •9.4 Влияние конденсаторных батарей на устойчивость узла нагрузки
- •12.1 Применение метода площадей для анализа динамической устойчивости простых систем
Глава 9. Определение статической устойчивости
НАГРУЗКИ С ПОМОЩЬЮ ПРАКТИЧЕСКИХ КРИТЕРИЕВ
9.1 Определение статической устойчивости асинхронного двигателя
Критерий статической устойчивости асинхронного двигателя [9,13]

Где
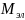 -
электромагнитный момент двигателя;
-
электромагнитный момент двигателя;
 -тормозной
момент механизма; s-
скольжение.
-тормозной
момент механизма; s-
скольжение.
При
постоянной частоте подводимого к
двигателю напряжения электромагнитный
момент равен в относительных единицах
мощности, передаваемой со статора на
ротор двигателя:
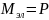 .
В свою очередь эта мощность может быть
найдена из упрощенной схемы замещения
асинхронного двигателя (АД) по формуле
.
В свою очередь эта мощность может быть
найдена из упрощенной схемы замещения
асинхронного двигателя (АД) по формуле
P=
 ,
,
Где
U-
напряжение на выходах двигателя; R-
сопротивление ротора при s=1;
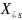 -
сопротивление рассеяния статора и
ротора.
-
сопротивление рассеяния статора и
ротора.
Из приведенной формулы видно, что мощность двигателя при U= const является функцией скольжения. Тормозной момент механизма, приводимого во вращение двигателем, в большинстве случаев зависит от скольжения.
Обычно
приходится рассматривать не один
асинхронный двигатель, а группу
двигателей, и представлять их в виде
одного эквивалентного двигателя. В этом
случае определение характеристики
в функции скольжения
s
затруднительно. Поэтому характеристику
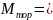 f(s)
считают горизонтальной и полагают
f(s)
считают горизонтальной и полагают
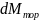 /
ds=
0. При этом критерий устойчивости АД
принимает вид
/
ds=
0. При этом критерий устойчивости АД
принимает вид
 . связанная с этим неточность создает
некоторый дополнительный запас
устойчивости.
. связанная с этим неточность создает
некоторый дополнительный запас
устойчивости.
В
предельном, с точки зрения устойчивости,
режиме АД определяются критическое
скольжение
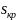 ,
максимальная мощность
,
максимальная мощность
 ( опрокидывающий момент) и критическое
напряжение
( опрокидывающий момент) и критическое
напряжение
 . При использовании этих параметров
необходимо иметь в виду следующее. При
несоизмеримо большой мощности системы
(источника питания нагрузки) в сравнении
с мощностью АД характеристику АД P=
f(s)
можно
строить при постоянстве напряжения на
выводах АД, не считаясь с потерей
напряжения в индуктивном сопротивлении
. При использовании этих параметров
необходимо иметь в виду следующее. При
несоизмеримо большой мощности системы
(источника питания нагрузки) в сравнении
с мощностью АД характеристику АД P=
f(s)
можно
строить при постоянстве напряжения на
выводах АД, не считаясь с потерей
напряжения в индуктивном сопротивлении
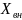 внешней сети при изменении скольжения
АД, т.е. приняв
=0.
В этом случае критическое скольжение
определяется по формуле
внешней сети при изменении скольжения
АД, т.е. приняв
=0.
В этом случае критическое скольжение
определяется по формуле
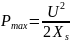 ,
а критическое напряжение- по формуле
,
а критическое напряжение- по формуле
 ,
где
,
где
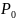 -
нагрузка двигателя. При питании двигателя
от шин с
-
нагрузка двигателя. При питании двигателя
от шин с
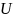 -
const
величина
примерно вдвое превышает номинальную
мощность двигателя, что обеспечивает
более чем достаточный запас устойчивости.
При напряжении
-
const
величина
примерно вдвое превышает номинальную
мощность двигателя, что обеспечивает
более чем достаточный запас устойчивости.
При напряжении
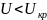 двигатель опрокидывается. Величина
служит показателем степени устойчивости
двигателя. Чем выше
,
тем менее устойчив двигатель. Критическое
напряжение, а следовательно, и запас
устойчивости двигателя зависят
существенно от загрузки двигателя m=
/
двигатель опрокидывается. Величина
служит показателем степени устойчивости
двигателя. Чем выше
,
тем менее устойчив двигатель. Критическое
напряжение, а следовательно, и запас
устойчивости двигателя зависят
существенно от загрузки двигателя m=
/ :
=
:
= , где
-
активная номинальная мощность асинхронного
двигателя.
, где
-
активная номинальная мощность асинхронного
двигателя.
Если
же мощность эквивалентного АД соизмерима
с мощностью системы, то напряжения на
выводах АД не остается постоянным, а
падает с увеличением скольжения в связи
с потерями напряжения во внешнем
индуктивном сопротивлении
.
В этом случае P=
f(s),
,
определяют при постоянстве эквивалентной
ЭДС
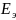 системы:
системы:
 ;
;

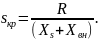
Критическая эквивалентная ЭДС определяется по формулу
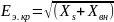 ,
где
-внешнее
сопротивление.
,
где
-внешнее
сопротивление.
Коэффициенты
запаса устойчивости АД можно определять
отношением мощностей
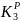 ,
отношением напряжений
,
отношением напряжений
 ,
ЭДС
,
ЭДС
 или скольжением
или скольжением
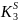 .
Чем больше значения этих коэффициентов,
тем больше надежность установившегося
режима АД.
.
Чем больше значения этих коэффициентов,
тем больше надежность установившегося
режима АД.
Пример 9.1. на рис. 9.1 изображена подстанция, связанная с системой С. К шинам вторичного напряжения трансформатора Т подключена нагрузка, которая представлена в виде эквивалентного АД. Номинальная мощность АД
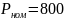 кВт,
она намного меньше мощности системы.
Номинальное напряжение на шинах нагрузки
кВт,
она намного меньше мощности системы.
Номинальное напряжение на шинах нагрузки
 кВ. двигатель работает с коэффициентом
загрузки m=1.
Номинальный коэффициент мощности
эквивалентного АД
кВ. двигатель работает с коэффициентом
загрузки m=1.
Номинальный коэффициент мощности
эквивалентного АД
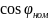 =0,8.
Параметры двигателя в относительных
единицах при номинальных условиях
следующие: суммарное сопротивление
рассеяния обмоток статора и ротора
=0,8.
Параметры двигателя в относительных
единицах при номинальных условиях
следующие: суммарное сопротивление
рассеяния обмоток статора и ротора
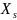 =0,1;
сопротивление намагничивания
=0,1;
сопротивление намагничивания
 ;
активное сопротивление R=
f(s).
;
активное сопротивление R=
f(s).
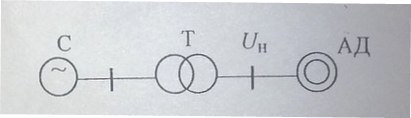
Рис.9.1
Решение
Поскольку
мощность двигателя намного меньше
мощности системы, то можно принять
 =const,
=const,
 .
Расчеты проведем в относительных
единицах. За базисные величины примем
номинальные данные двигателя: мощность
.
Расчеты проведем в относительных
единицах. За базисные величины примем
номинальные данные двигателя: мощность
 ,
напряжение
,
напряжение
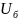 =10
кВ. при этих условиях
=1,
нагрузка АД
=10
кВ. при этих условиях
=1,
нагрузка АД
 =
=
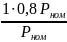 =0,8. Параметры АД остаются такими же,
какие даны в условии задачи. Схема
замещения асинхронного двигателя
показана на рис. 9.2.
=0,8. Параметры АД остаются такими же,
какие даны в условии задачи. Схема
замещения асинхронного двигателя
показана на рис. 9.2.
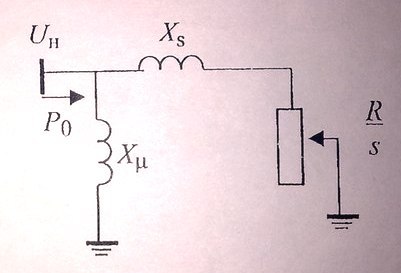
Рис. 9.2
Определим
максимальную мощность АД


Коэффициент запаса устойчивости АД по мощности
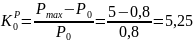
Для определения коэффициента запаса устойчивости по скольжению
Необходимо
вначале найти величину скольжения
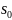 АД при нагрузке
АД при нагрузке
 эту величину
эту величину
 из
выражения
из
выражения

После соответствующих преобразований получим уравнение
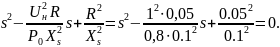
Решив
это уравнение относительно s,
получим
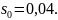
Определим критическое скольжение
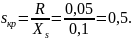
Коэффициент запаса устойчивости АД по скольжению

Найдем критическое напряжение

Коэффициент запаса устойчивости АД по напряжению

где

Для построения кривой P=f(s ) определяется еще одна точка при s=1 (неподвижном двигателе).
Кривая
P=f(s
)
представлена на рис. 9.3 при допущении,
что параметры АД не меняются. Здесь
 =4.
=4.
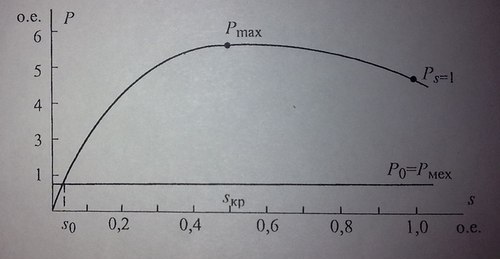
Рис. 9.3
Точка
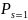 =14
(рис.9.3) соответствует начальному
пусковому моменту. Полученное значение
свидетельствует о возможности пуска
АД при нагрузке
=0,8.
=14
(рис.9.3) соответствует начальному
пусковому моменту. Полученное значение
свидетельствует о возможности пуска
АД при нагрузке
=0,8.
На
рис.9.3 представлена зависимость P=f(s
)
при
 Аналогично можно получить зависимость
P=f(s
)
и при других значениях
Аналогично можно получить зависимость
P=f(s
)
и при других значениях

Вывод.
АД обладает большим запасом устойчивости.
Наиболее характерной величиной при
этом является коэффициент запаса
устойчивости по напряжению
 Снижение напряжения в системе на 60
Снижение напряжения в системе на 60
Пример
9.2.
Станция Г через трансформаторы Т1,Т2,
линию электропередачи Л питает нагрузку,
которая представлена на рис.9.4 в виде
эквивалентного АД. Мощность станции Г
соизмерима с мощностью АД. На станции
установлены генераторы с автоматическим
регулятором возбуждения (АРВ)
пропорционального действия. Параметры
системы рис.9.4 в относительных единицах
равны: сопротивление рассеяния статора
и ротора АД
 сопротивление
R=0.05;
сопротивление намагничивания АД
сопротивление
R=0.05;
сопротивление намагничивания АД
 ;
суммарное сопротивление трансформаторов
Т1,Т2, линии Л
;
суммарное сопротивление трансформаторов
Т1,Т2, линии Л
 ;
переходное сопротивление
генератора
;
переходное сопротивление
генератора
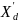 =0,15.
Нагрузка АД P0
=
0,8, напряжение на шинах нагрузки Uн
=
1.
=0,15.
Нагрузка АД P0
=
0,8, напряжение на шинах нагрузки Uн
=
1.
Требуется определить коэффициент запаса статической устойчивости АД по мощности , скольжению и напряжению .
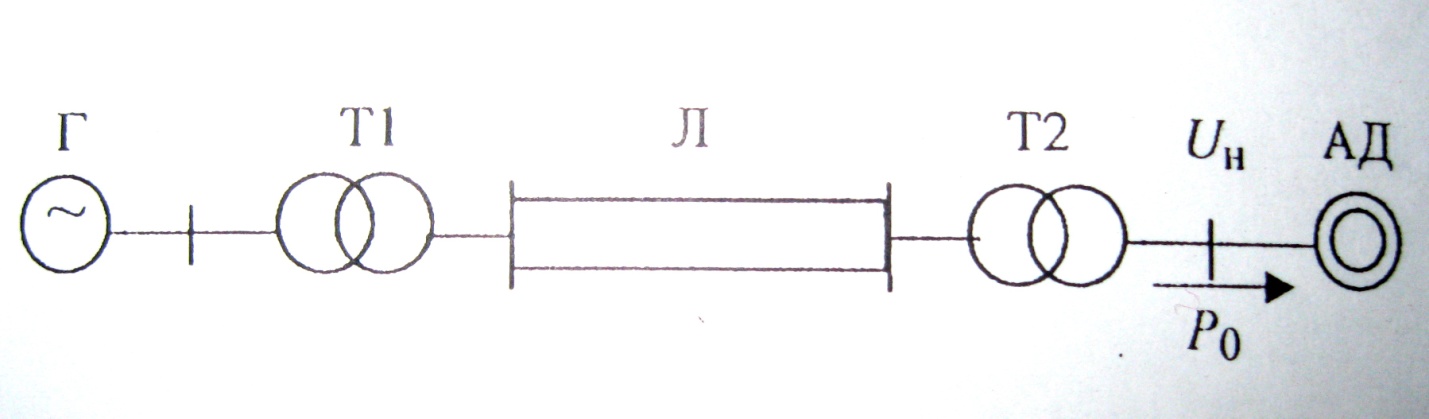
Рис.9.4
Решение
В данном случае напряжение на шинах нагрузки Uн зависит от режима двигателя. Независимой является ЭДС генератора. Поэтому в схеме замещения системы (рис. 9.5) учувствуют сопротивление генератора и Xc . При составлении схемы замещения (рис. 9.5) ветвью намагничивания АД пренебрегаем.
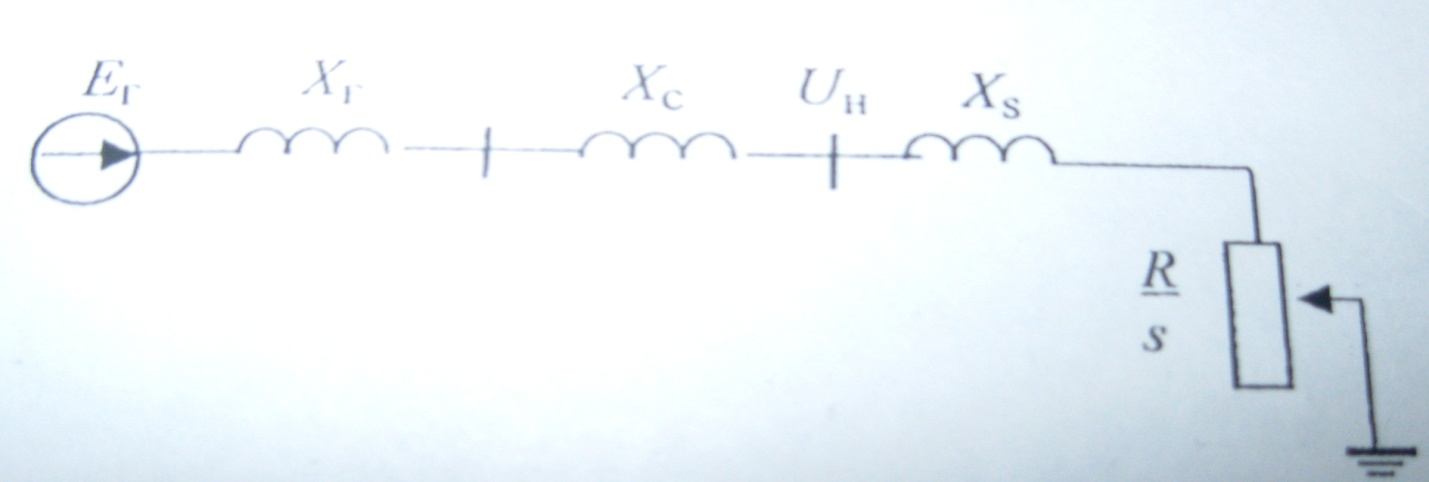
Рис. 9.5
Так
как генераторы имеют АРВ пропорционального
действия, то Ег
=
 и
Хг
=
. Для определения переходной ЭДС
необходимо определить реактивную
мощность Q0
, потребляемую АД при Uн
=1.
Эту мощность можно определить по формуле
и
Хг
=
. Для определения переходной ЭДС
необходимо определить реактивную
мощность Q0
, потребляемую АД при Uн
=1.
Эту мощность можно определить по формуле
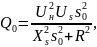
где s0 – скольжение АД в исходном режиме при Uн = 1 и при Р0 = 0,8. Это скольжение было определено при решении задачи 9.1, оно равно 0,04. Таким образом, Q0, соответствующее s0, равно:

Тогда
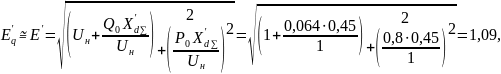
где

Максимальная мощность

Коэффициент запаса устойчивости АД по мощности

Критическое скольжение
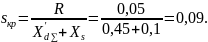
Коэффициент запаса устойчивости АД по скольжению

Критическая ЭДС генератора

Коэффициент запаса устойчивости АД по ЭДС
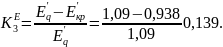
Определим
критическое напряжение
на
шинах нагрузки при
 .
Для этого найдем значение реактивной
мощности
.
Для этого найдем значение реактивной
мощности
 ,
выдаваемой генератором.
,
выдаваемой генератором.
В общем случае в предельном режиме реактивная мощность АД численно равна активной мощности . Для доказательства этого положения рассмотрим простую схему замещения АД (рис. 9.6).
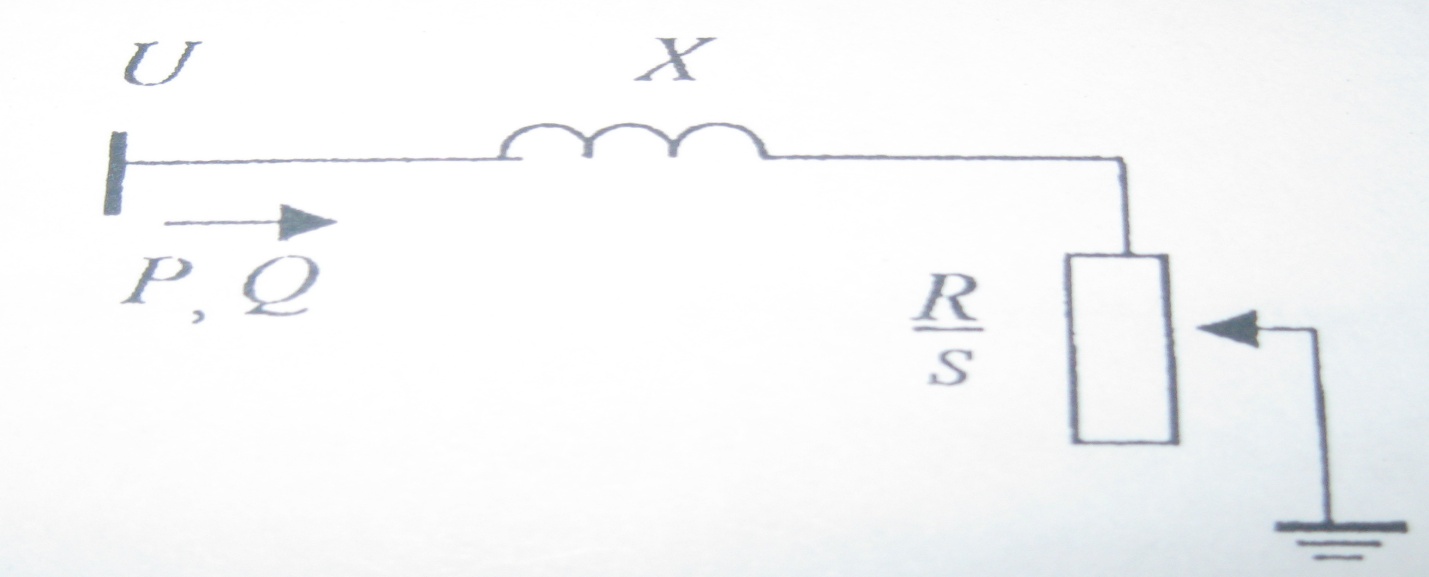
Рис. 9.6
Реактивная мощность определяется по формуле

В
предельном режиме при скольжении
 реактивная мощность
реактивная мощность

При
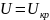
 . Следовательно,
. Следовательно,
 в предельном режиме.
в предельном режиме.
Таким
образом, при
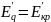
 . Тогда
. Тогда
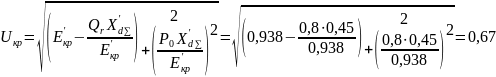
Коэффициент запаса устойчивости АД по напряжению

Вывод: при соизмеримой мощности генератора и двигателя устойчивость последнего ухудшается.
